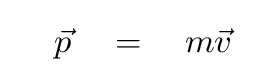
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The regular old low-velocity expression for momentum
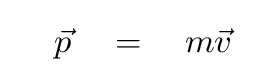
doesn't work when objects move with relativistic speeds. Why not? Well, consider a proton, which has m = 1.67 x 10^(-27) kg. Suppose that we put the proton into an accelerator and push it forward until it gains some momentum. How fast will it be going?
Q: If we give the proton a momentum
p = 4 x 10^(-19) kg*m/s
what will its speed v be?
Express in terms of c.
Q: If we give the proton a momentum
p = 8 x 10^(-19) kg*m/s
what will its speed v be?
Express in terms of c.
Whoops! That's a problem. It should not be possible to accelerate objects with mass to the speed of light, let alone to superluminal speeds.
It turns out that there is a slightly different expression for momentum which must be used when objects are moving at relativistic speeds. I won't derive it here; you can look at Taylor and Wheeler's book Spacetime Physics for the details if you wish. The result is
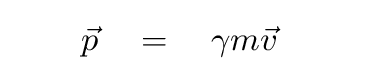
Q: Now use the relativistic expression
for momentum. If we give the
proton a momentum
p = 8 x 10^(-19) kg*m/s
what will its speed v be?
Express in terms of c.
(Having trouble isolating the
speed v? Maybe you should
peek at a bit of algebra. )
If a particle is moving at very high speeds, so that its velocity v is almost equal to c, then the relativistic expression for momentum will be approximately
Note how similar these two expressions are.
It appears that we can almost turn momentum into energy, using c.
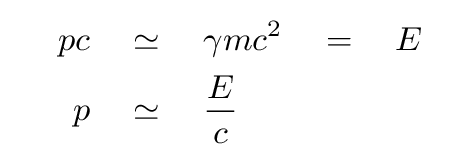
How good is this approximation? Well, it depends on how relativistic the particle happens to be. Consider an electron, which has mass m = 9.1 x 10^(-31) kg = 0.511 MeV / c^2.
Q: Two electrons are sent through an accelerator.
Electron A has total energy
A: 1 MeV = 1.6 x 10^(-13) J
but electron B has total energy
B: 1 GeV = 1.6 x 10^(-10) J
For each electron,
what is its gamma factor?
what is its velocity?
what is its momentum?
How close does (momentum times c) really
come to the total energy?
The connection between momentum and total energy
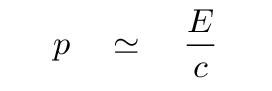
works best for particles which are moving at speeds very close to c, so that their gamma factors are very large. Under these hyper-relativistic conditions, the total energy
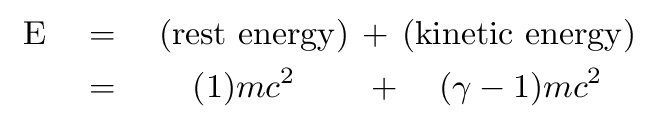
is almost completely kinetic energy, with only a tiny contribution from rest energy. The closer the speed is to c, the larger the contribution from kinetic energy, and the closer the relationship is to perfect equality.
Suppose that we take it to the limit: what if a particle was moving with the speed of light? In that case, we should expect that the total energy would be ENTIRELY kinetic, and the momentum should be EXACTLY
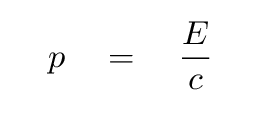
"Wait a minute!" you might cry. "That's impossible! Objects with mass cannot travel at the speed light!"
Correct. Objects with mass can't travel at the speed of light. But what about objects without mass? In particular, what about PHOTONS?
And so there is a perfect relationship between the energy of a photon and its momentum. Yes, photons DO have momentum, even though they have no mass!
As you will learn in a modern physics course, the energy of a photon is related to its wavelength and frequency via Planck's constant h = 6.626 x 10^(-34) kg*m2/s .
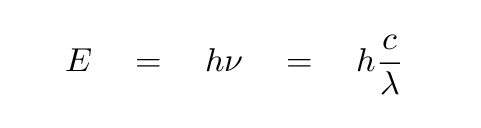
Q: A photon of yellowish light has wavelength lambda = 550 nm,
in the middle of the human visual range.
What is the energy of the photon?
What is the momentum of the photon?
Hmmmm. That doesn't sound like much momentum. However, photons are cheap; the Sun produces many, many, MANY photons each second. A pretty large number of those photons zip through space past the Earth every second. In fact, if one goes up above the Earth's atmosphere, very roughly 3.8 x 10^(21) yellowish photons will pass through an area one meter on a side oriented face-on to the Sun.
Joe places a very thin square of black plastic
into space. The plastic is 1 meter long
by 1 meter wide, and absorbs every photon
which strikes it. It has a mass of 0.1 kg.
Q: How much momentum is transferred to
Joe's plastic in one second?
How much momentum is transferred to
Joe's plastic in one hour?
Q: (Ignore the force of gravity for now)
If the plastic square was originally
motionless, what is its velocity after
one hour?
The momentum of photons from the Sun provide the thrust for solar sails, which may be used in future space missions. Solar sails provide very, very small values of thrust, so they can accelerate payloads only gradually. However, they don't require any fuel.
The Japanese Aerospace Exploration Agency (JAXA) launched a solar sail called "IKAROS" in 2010.
Go to 1:00 in program
A proper treatment of solar sails does require the inclusion of gravitational forces. If you wish, you may try an extra credit project on solar sails.
An invariant quantity is one that has the same value, no matter which observer is making measurements. The space-time interval
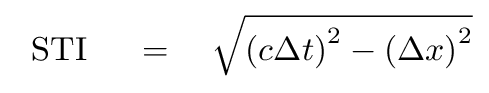
is an example of an invariant quantity.
Is the relativistic version of momentum an invariant quantity? Let's find out.
The Blue Man throws a ball (m = 0.2 kg ) at a speed of v = 0.5 c to the right.
Q: What is the momentum of the ball,
according to the Blue Man?
But the Blue Man and the ball are all travelling across the landscape at a speed of w = 0.8 c to the right, as measured by the Red Men.
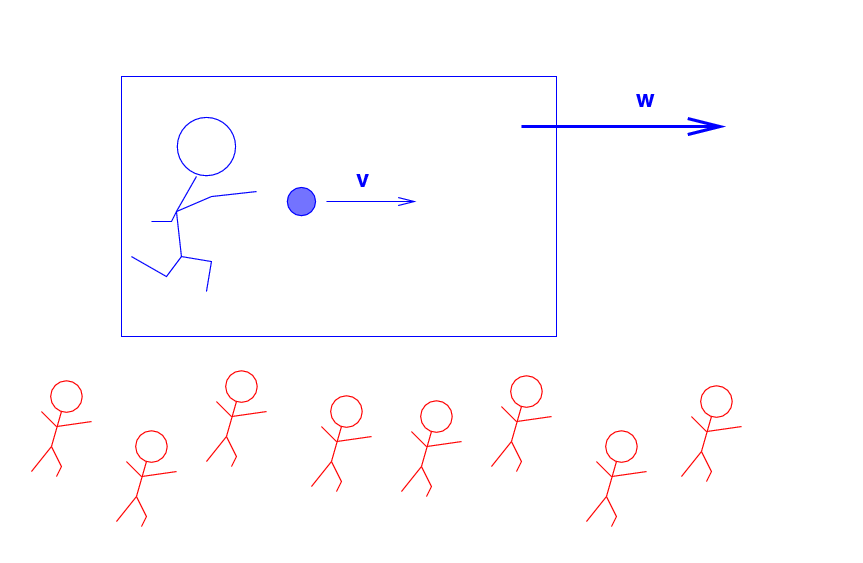
Q: What is the momentum of the ball,
as measured by the Red Men?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.