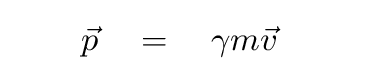
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Suppose you know the mass m of a particle, and you are given its momentum p. If the particle is moving at high speed, then its momentum is related to its velocity v like so:
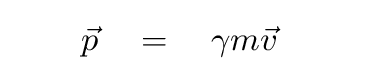
If you try to solve for the velocity v, you might think yourself stumped after the first step:

"Oh noes!" you might say, "I can't isolate the velocity v, because gamma has the velocity inside it."
Don't despair. You CAN still isolate the velocity; you just need to do a bit of algebra. Let me lead the way.
It would be annoying to have to keep writing p/m in all the following steps, so I'll define a single variable to hold that ratio of momentum to mass.
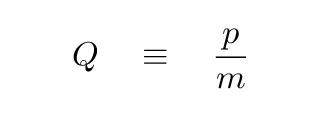
So our problem now looks like this:
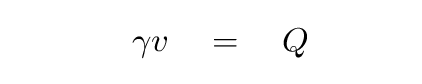
A good first step is to square both sides, so that we get rid of the square root inside the expression for gamma.
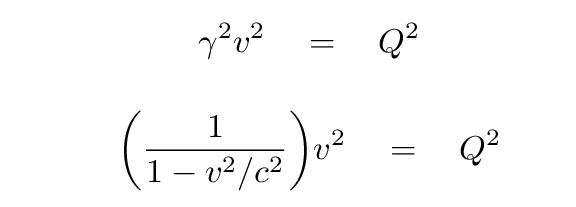
Now, let's multiply both sides by (1 - v^2/c^2).
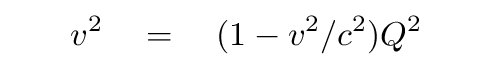
We can put all the terms with v together on the left ...
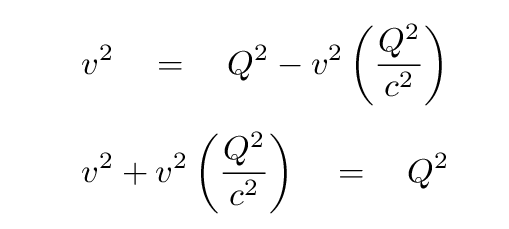
... and then isolate the velocity v.
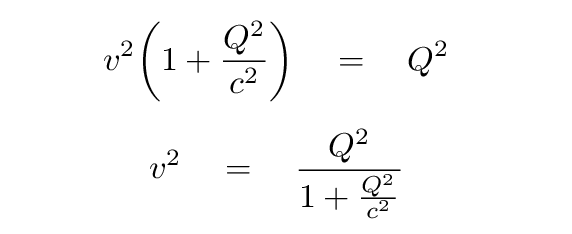
We end up with an expression for velocity of a relativistic particle, given its mass m and momentum p:
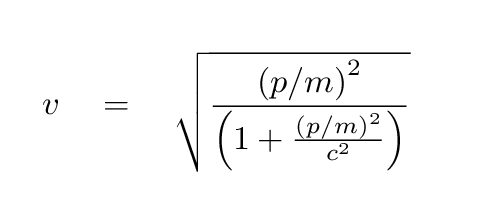
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.