Practice problems for the final exam

  1. The Space Police are worried. A mysterious object with the same mass as the Earth's moon has entered the solar system, moving at 10 km/s toward the inner planets. Who's responsible?

    Lieutenant Jones reports to Inspector Smith. "We have two suspects, a Romulan ship and a Klingon freighter. Both claim to be travelling at constant speed and direction through the relativistic shipping lanes, though the Klingons are moving much faster. We asked the captain of each ship what she knew about the mystery object. The Romulan captain reported that it had a total energy of 7.63 x 1039 Joules, and the Klingon captain said the total energy was 1.52 x 1040 Joules."

    Smith grunts. "That's consistent with what we know about their speeds. Did they say anything about the momentum of the object?"

    Jones answers, "Yes, we questioned their science officers. The Romulans measure 1.27 x 1031 kg*m/s, and the Klingons report 3.25 x 1031 kg*m/s."

    Smith thinks for a moment, then slams his fist on the table. "That's it! We've got them!"

    1. Who is lying?
    2. How do you know?

    Answers to Problem 1

  2. The New York Thruway police have a problem: special souped-up electric vehicles are starting to drive down the roads at relativistic speeds. Their plan is to use the Wi-Fi signals emitted by the cars (because EVERYONE has Wi-Fi) to determine if a car is speeding. The rest frequency of Wi-Fi is 2.4 GHz.

    On a long, straight, East-West stretch of the highway near Rochester, the police have two options: they can place a monitoring station hidden in a clump of trees, about 100 meters to the south of the road, and measure the frequency of cars going past that spot; or, they can place a squad car in the median strip, at the far eastern end of the straight section, and measure the frequency of cars coming toward the officer there.

    1. Suppose a car drives East at v = 0.7c. What is the frequency measured by each squad car?
    2. Suppose that a car drives at only slightly-relativistic speeds, around 0.05 c. Can you prove mathematically that one location is always a better choice than the other?

    Answers to Problem 2

  3. Joe turns 20 years old, but wants more out of life. He hears that if one moves at high speed, one's clocks will run slow, and one will live longer than stationary people. So, he decides to get in his car and drive at v = 50 mph for the rest of his life. Thanks to drive-through fast-food restaurants, Joe lives for another 60 years, always driving at a constant speed and direction; and he DOES end up living a little bit longer than everyone else.
    1. How much longer?

    Answers to Problem 3

  4. In the space-time diagram above (you can click here for another copy), each red box represents one meter of time, or of space, as measured by the stationary observers Bob and Jane. Refer to the actors and events on the diagram, and use it to help you answer the questions below.
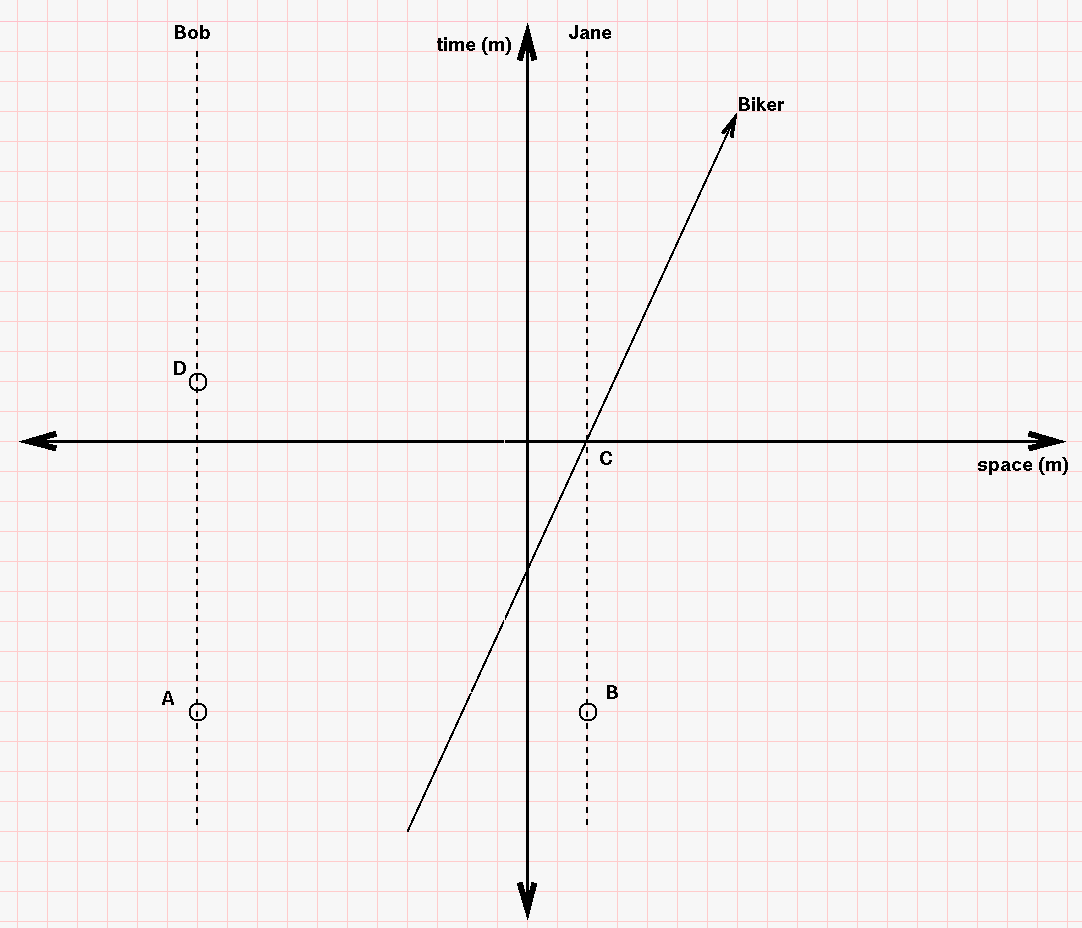
    1. How fast is the biker cruising to the East?

      2. Points "A" and "B" represent the alarm clocks of Bob and Jane both going off, and point "C" is when the Biker passes Jane. At "C", the Biker's clock reads 5 m.

    2. What is the time interval between events "A" and "B" according to Bob?
    3. What is the time interval between events "A" and "B" according to the Biker?
    4. What is the time interval between events "B" and "C" according to Jane?
    5. What is the time interval between events "B" and "C" according to the Biker?

      6. The biker flashes his taillight at some time before he passes Jane. The flash of red light reaches Bob at point "D".

    6. When did the Biker flash his taillight, according to Bob?
    7. When did the Biker flash his taillight, according to the Biker?

    Answers to Problem 4

  5. The center of the Milky Way Galaxy is roughly 8000 parsecs away from the Earth. In the book "A World Out of Time," Jaybee Corbell flies a spaceship from Earth to (roughly) this location, then returns to the Solar System. On the ship, about 150 years pass; Corbell survives because he enters "deep frozen sleep" for most of the journey. On the Earth, about three million years pass. Assume that Corbell makes a simple round trip, straight to the center and then straight back, at a constant speed v.

    1. Assume further that the difference in time passing for Corbell and Earth-people is due entirely to the time dilation factor. Based on the time differences, how fast was Corbell flying?
    2. Now, using that speed, compute how long a simple round trip to the galactic center SHOULD have taken (in other words, compute the Earth time based on the distance travelled and speed).
    3. Do you see any problem here?

    Answers to Problem 5