Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
This is the third in a series on the "Twin Paradox".
Today, we'll look at several representations of the tiwn paradox in popular media.
Image and video of "Lightyear" courtesy of Walt Disney Studios
In this movie, the Space Ranger Buzz Lightyear and a team of explorers are stranded on a uncharted planet. Their spaceship is damaged, and their only hope of escape is to create a new type of fuel. In order to the test the fuel, Buzz undergoes a series of test flights in which he flies the ship (alone) at very high speed in a loop around the planet's host star.
His average speed during this flight is roughly 0.5 c, and according to his clocks, the flight lasts about 4 minutes.
Q: What is the gamma factor for Buzz?
Q: How much time should elapse on the planet from the time
he leaves until the time he returns?
When Buzz returns to the base, he finds that people there have experienced much more time than he did. MUCH more time. In fact, they measured his flight to last 4 years.
Q: What gamma factor would be required to make this happen?
Q: How fast would Buzz' ship have to travel to achieve such
a large gamma factor?
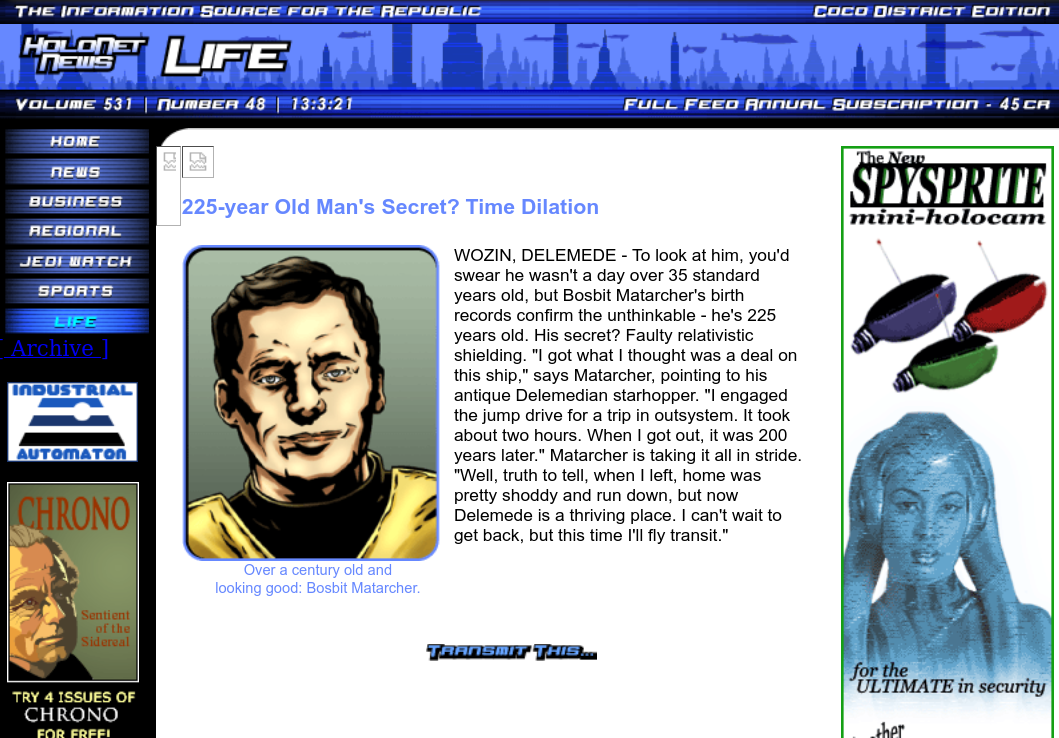
HoloNet News item provided courtesy of
The Internet Archive's Wayback Machine
It's a simple story: Bosbit took a 2 hour tour (a two-hour tour) on his ship, but, due to the faulty "relativistic shielding", his journey took 200 years according to the people on his home planet.
Q: What gamma factor would be required to make this happen?
Q: How fast would Bosbit's ship have to travel to achieve such
a large gamma factor?
Q: What is "relativistic shielding"?
Image and video clip from the original "Planet of the Apes"
courtesy of
FoxInternationalHEKR
During this initial phase of their journey, the astronauts (led by Captain Taylor, played by Charlton Heston) have travelled at speeds close to the speed of light. Although their clocks show only 6 months have passed, the clocks back on Earth have registered 700 years.
Q: What gamma factor would be required to make this happen?
Q: How fast would Taylor's ship have to travel to achieve such
a large gamma factor?
Q: Is it really a good idea to smoke cigars inside a spaceship?
Image and video clip from "Interstellar"
courtesy of
Legendary Movie Scenes
The Earth is undergoing a catastrophic environmental change, which will make it hostile to humans in a relatively short time. A small crew of astronauts heads out into space to look for a planet to which humans can move. In the scene above, the crew discusses the possibilities of several planets which are close to a supermassive black hole.
One of these, called "Miller's Planet", is promising: it has an atmosphere humans can breathe, and a large amount of water. However, exploring it does involve a risk: because the planet is so close to the black hole, time will run slower for anyone on or near the planet, compared to those who are far from the planet (and from the black hole). As Romilly points out, "every hour we spend on that planet will be seven years back on Earth."
Now, this time dilation is NOT due to Special Relativity! Instead, this is a consequence of Einstein's theory of GENERAL Relativity (GR), which deals with the effects of strong gravitational fields. The mathematics of GR are much more complex than those of special relativity, so I'm not going to try to explain them. However, I can provide one very simple equation which may give you a flavor for the nature of this sort of time twisting.
Imagine two observers, A and B, one of whom (A) is located near a massive object, while the other (B) is far, far away. In this situation, A will experience a stronger gravitational field than B, and so A's clocks will appear to run more slowly. In the simplest possible case of a spherically symmetric, static, uncharged body, the relationship between time intervals measured by these two observers can be calculated as
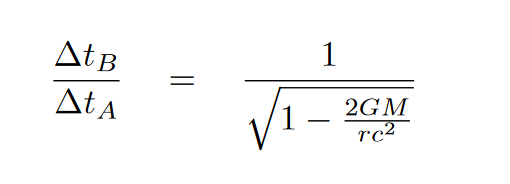
where
gravitational constant G = 6.67 x 10-11 (N * m2 / kg2) mass of object M (kg) distance of A from object r (m) speed of light c = 299,792,458 (m/s)
Let's try a simple example to see how this might affect astronauts far from the Earth -- say, on a trip to Saturn. Use "A" to denote a person living on the Earth, and "B" to denote an astronaut very far from the Earth. In this case, M = 5.98 x 1024 kg and r = 6.37 x 106 m.
Q: What is the ratio of time intervals (the gravitational time
dilation factor) between the clocks of A and B?
Q: If the astronaut has been away from Earth for 10 years,
how different are his clocks compared to those
on the Earth? In other words, how much more time
has he measured? Express your answer in seconds.
This equation cannot be used to analyze the situation in Interstellar properly, because the black hole in the movie is not static, but spinning very, very rapidly. That adds complications which are beyond the scope of this class. If you'd like to read more about it, consider looking at
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.