 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Many of you have heard of the "Twin Paradox". It goes something like this:
Joe and Bob were twins, born on Jan 1, 2480, and raised on Earth. When they were both 20 years old, Joe joined the Space Navy and travelled at relativistic speeds to a distant colony. When Joe returned home, he was only 30 years old ... but Bob was now an old man!
It is an easy matter to compute the age of each twin if we are given the speed of the traveller. However, understanding WHY one twin ages so much, and other so little, is a more difficult task. We will take several lectures to work our way through the problem.
Today's lecture will focus on the out-bound trip, as Joe moves away from the Earth at high speed.

Federation scientists on each planet have built accurate clocks. They synchronize all the clocks using powerful laser beams which can reach from one planet to another.
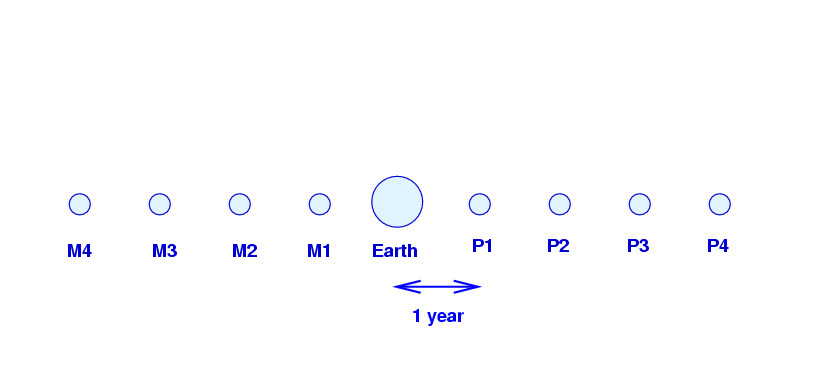
The Federation Navy has a special fleet of red supply ships which travel through space with a constant speed v = 0.9c. There are many, many ships, all moving in a line, one after the other. The ships keep their clocks synchronized with each other.
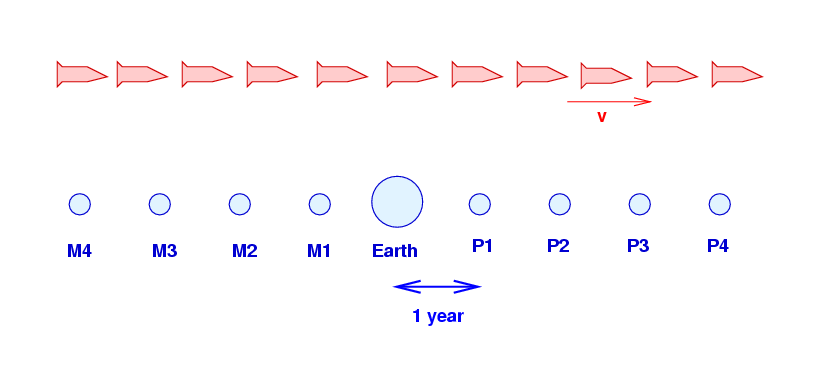
On Jan 1, 2500 -- when Joe and Bob both turn 20 years old -- Joe hops onto a shuttle which takes him to the Navy cruiser called Red Flagship, which is just passing the Earth at that moment. The Admiral of the Red Fleet is on board this ship, and as it passes the Earth, the Admiral's clock also reads Jan 1, 2500.
So, Joe and Bob and Earth and all the planets and the Red Flagship (but not the rest of the Red Fleet!) have clocks and calendars which all read Jan 1, 2500, when Joe joins the Flagship. Let's agree to keep track of time in a simple way: we'll call this moment "the start" or t = 0, and measure other events relative to it. Let's use years to measure time, and years (light-years) to measure space.
Joe and Bob agree to send each other regular messages on their birthdays. In other words,
After travelling on the ship for some time, Joe reaches planet P1. The ship doesn't slow down or stop, but it does exchange radio messages with the planet. It also picks up some supplies from a high-speed shuttle craft.
Q: According to people on planet P1
(or on the Earth, or on any planet),
what is the time and location
of this event?
Q: According the Joe,
what is the time and location
of this event?
Okay, that wasn't so difficult. If we compare the time intervals between events 0 and 1, we find that the planet-based observers measure a longer time interval than Joe.
So, can you come up with answers to these more these general questions?
Q: By what factor is Joe's clock
running slow, according to the planet-based
observers?
Q: What is the distance between planets,
according to Joe and the crew
of the ship?
Common sense suggests that if the planetary observers see Joe's watch running too slow, then Joe will see the planet-based clocks running too fast. But can we trust our common sense in a relativistic situation? Hmmmm.
It will help if we consider measurements made by sailors aboard a different red ship. In particular, let's consider the red ship which happens to be flying past the Earth just as people there celebrate the New Year of Jan 1, 2501, exactly one year after Joe left the Earth.
Q: What is the time and location of
this celebration, according to the
planet-based observers?
Q: What is the time and location of
this celebration, according to the
Red Navy ship which is passing by?
So, exactly one year has passed according to people on the Earth: it is now New Year's Day of 2501. But, according to the sailors aboard the Navy ship, it has been more than one year since Joe began his journey.
Q: By what factor is the Earth's clock
running slow, according to Navy-based
observers?
Phew. According to each set of observers, the clocks of the OTHER group -- which are flying past at relativistic speeds -- are running slowly. There is no asymmetry in the situation (yet).
"Wait a moment!" you might say at this point. "How can both sets of observers deduce that the other team's clocks are running slowly?"
Look carefully at what the planet-based people should conclude. They determined that that the clocks on board the Red Navy were running slower than planet-based clocks, but they also saw that the Navy ship which zipped past on New Year's Day, 2501, claimed that it was more than two years since the Red Flagship left the Earth.
The only way to reconcile these two observations is for the planet-based observers to conclude that the clocks on board different Red Navy ships are not synchronized properly. In other words, the planet-based observers would say that an event which takes place on Jan 1, 2500, according to the Red Flagship, would occur at a different time as measured by a different Red Navy ship. According to the planetary time system, the Red Navy's clocks are all shifted relative to each other.
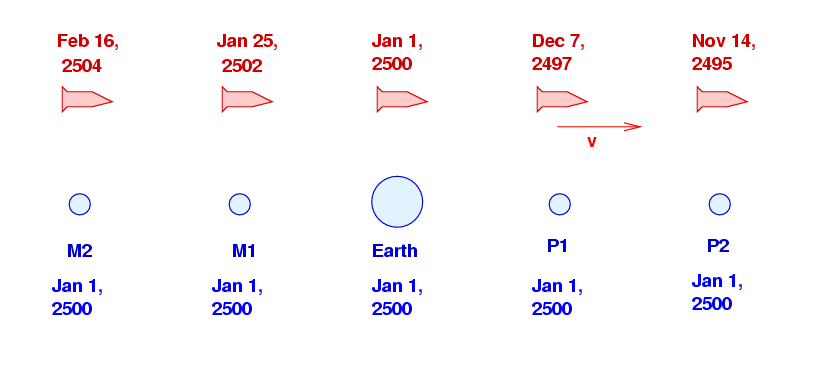
But according to the Red Navy's time system, it is the clocks on different planets which are offset from each other.
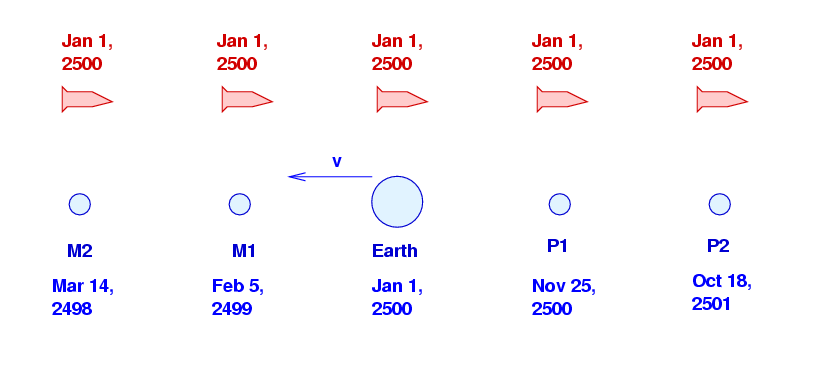
This is just the relativity of simultaneity in a new guise.
Please use a piece of graph paper to create a space-time diagram of the situation. Make sure that your graph runs along the space (horizontal) axis from 0 to 11, and along the time (vertical) axis from 0 to 12.
On this space-time diagram, mark the following items:
0. Joe leaves the Earth aboard the
Red Flagship, on his twentieth
birthday.
1. The Red Flagship travels to
planet P10 (draw the worldline
of the ship).
2a. When Joe has his first birthday
aboard the ship, he sends a
radio message back to Bob.
2b. The message reaches Bob.
3a. When Joe has his second birthday
aboard the ship, he sends a
radio message back to Bob.
3b. The message reaches Bob.
4a. When Bob has his first birthday
since Joe left, Bob sends a radio
message to Joe.
4b. The message reaches Joe.
If you don't finish your space-time diagram today, please complete it before our next class, and bring it with you then.
Take a peek at a copy of my diagram (PDF)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.