 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You have the tools to figure out how to convert measurements of intervals between events from one inertial reference frame to another inertial reference frame. For example, if someone asks
Q: Fred stands in the lab. He sneezes. Twenty
seconds later, he sneezes again.
Jane and her friends fly past the lab at
a speed of v = 0.8c. What is the
interval between Fred's sneezes according
to them?
a) 20 seconds
b) 16 seconds
c) 12 seconds
you can figure out the answer.
However, there are times when dealing with intervals is awkward. Sometimes, you'll need to convert a bunch of individual measurements from one reference frame to another.
Q: Fred stands in the lab, with John 10 meters
to his left and Larry 5 meters to his right.
Fred sneezes. Ten seconds later (according
to Fred), John sneezes. Thirty seconds later,
Larry sneezes.
Jane and her friends fly past the lab at
a speed of v = 0.8c. What are the
times and locations of all three sneezes
according to them?
Using the invariance of the space-time interval to do the conversions will work, but it can take a long time. It would be more convenient if we could find a simple algorithm for converting measurements made by observers in one inertial reference frame to those made by observers in a different inertial reference frame.
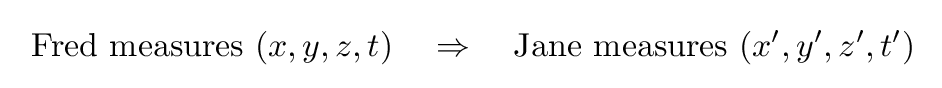
In other words, we would like to find a coordinate transformation which turns the measurements from one frame into corresponding measurements in the other frame. Let's look at two transformations:
Later on in this course, we'll be using the Lorentz transformations for the most part. However, over the next few years, as you wend your way through the physics curriculum, you'll usually be using the Galilean version. Why? Because most of the objects that most scientists study are moving at non-relativistic speeds, and they are simpler to use.
See, many scientists are pragmatic. If there's a method which is easy to use, and which yields results which are good enough, scientists will adopt it. It's only when the results are NOT "good enough" that we turn to the complicated versions.As Einstein wrote in "On the Method of Theoretical Physics", Philosophy of Science, Vol. 1, No. 2 (April 1934), pp. 163-169.
It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience.
or, in a shorter paraphrase which has become more well known,
Everything should be made as simple as possible, but no simpler.
Fred stands in his lab in Rochester. He measures the location and time at which events occur, and records them with the notation

Jane flies past on her SpaceLab, moving to Fred's right at a speed v.
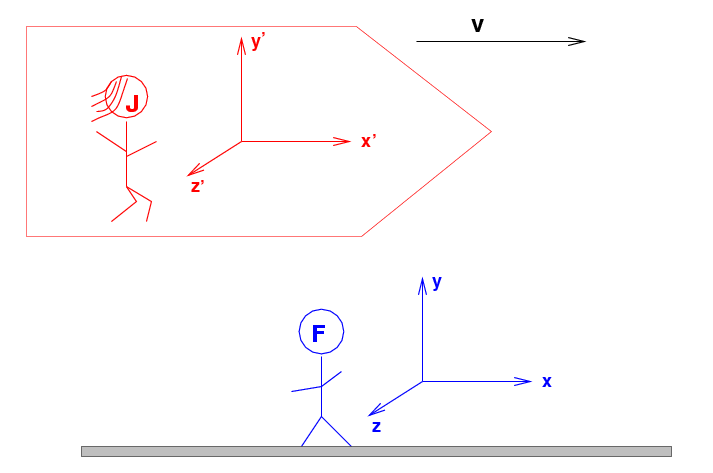
She (and her assistants, who are also moving at the same speed and in the same direction) measures events, but she records her values with the notation
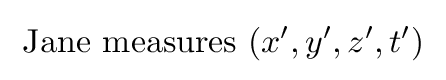
If we start with Fred's measurements, and we wish to calculate the values which Jane would determine, then we need some sort of mathematical expressions which involve
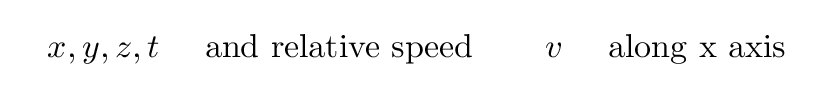
On the other hand, suppose that we start with the measurements made by Jane. From HER point of view, Fred and his team of observers are all moving to the LEFT at a speed v. In that case, we would start with the variables
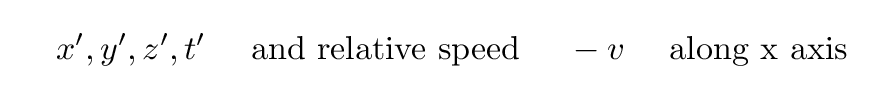
Our goal is to find a single set of equations which will work for both cases.
Fred stands in his lab in Rochester. Jane flies past at speed v in the positive x-direction, to the right. If the relative motion of the two inertial frames v is much less than the speed of light, then we can use the Galilean transformation to convert Fred's measurements into Jane's measurements.
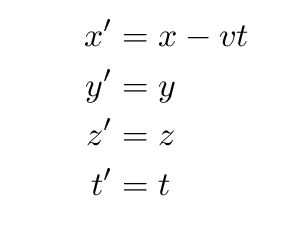
Q: What would we do if Jane was flying
past Fred in the other direction,
at speed v to the left?
Notice that the only change is in the x-component of the position of events. The time component is exactly the same for each observer. The idea that time flows independently of observers, in some absolute sense, is a very old one. Isaac Newton was drawing on classical traditions when he wrote in his Principia Mathematica
Absolute, true, and mathematical time, of itself, and from its own nature, flows equably without relation to anything external, and by another name is called duration: relative, apparent, and common time, is some sensible and external (whether accurate or unequable) measure of duration by the means of motion, which is commonly used instead of true time; such as an hour, a day, a month, a year.
Now, remember: these transformations yield the proper results when all the motions are small compared to c. Nonetheless, let us TRY to apply them to a situation in which that is not the case. Let's use them to see what they predict for two frames in relativistic motion. The results won't be right ... but I think this procedure will make things easier to understand later.
Fred stands on the ground in Rochester, in the middle of a big field. His team of students is spread out all over the field, with clocks synchronized and metersticks at the ready. Fred and his students watch as a series of events unfold.
Q: Make a space-time diagram which shows
all these events, as measured by
Fred and his team.
(Your diagram should cover at least
the region x = -4 to x = +11 meters
and t = -1 to t = 16 meters)
(You may consider just a few moments --
t = 5 and t = 10 meters, for example)
You can look at my graph if you wish.
Now, Jane and her team are also making careful measurements of these same events as they fly past at v = 0.3c to the LEFT. Use the Galilean transformations to figure out the locations and times of these events in Jane's frame of reference.
Compute the times and locations of the events as measured by Jane and her assistants on one of these worksheets.
Q: Make a (new) space-time diagram which shows
all these events, as measured by
Jane and her team.
You can look at my version of Jane's graph if you wish.
Look at your two diagrams to answer the following questions.
1. The long line of men raising their
hands lies along the x-axis in
Fred's space-time diagram.
Do those events also lie along the
x-axis in Jane's diagram?
2. The man with a bad cold lies
along the y-axis in Fred's diagram.
Does he also lie along the
y-axis in Jane's diagram?
3. Consider the cough and the sneeze.
What is the time interval between
these two events according to Fred?
According to Jane?
4. Consider these two events:
the bird chirps
the bird meets the dog
What is the time interval between
the events according to each observer?
What is the space interval between
the events according to each observer?
5. How fast is the bird flying,
according to Jane?
6. (optional) Where is the laser beam
at time t=11 seconds according to each
observer?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.