Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Image of Mercury courtesy of
MESSENGER, NASA, JHU/APL, CIW and
APOD
Image of Venus courtesy of
Mattias Malmer, from NASA/JPL data
Image of Earth from the DSCOVR satellite courtesy of
NASA
Image of Mars from HST courtesy of
NASA
I'm going add a bonus body to our discussion today, -- the Earth's Moon -- even though it's not one of the major planets. However, it will serve nicely to illustrate some of the concepts we'll discuss ...
Image of Moon courtesy of
Gregory H. Revera and Wikipedia
Some of the terrestrial planets DO have thick, plentiful atmospheres.
Q: Which ones have thick atmospheres?
Some of the terrestrial planets have NO ATMOSPHERE at all.
Q: Which ones have no atmosphere?
Why? What causes gas to hang around some planets, but leave others? The answer is a bit complicated, because it depends on a contest between two basic factors:
If gravity wins the contest, then molecules of gas will remain close to the planet's surface, and the planet will retain an atmosphere. But if the random motions win, then molecules will gradually, individually, fly off into space and never come back. Any atmosphere surrounding such a planet will eventually "leak" away and disappear.
So, which factor wins? In order to answer that question, we need to apply some rules from physics ... and we need to know some basic facts about the planet.
So, let's consider all these individual parameters, and then we can put them together to explain the current state of atmospheres among our terrestrial planets.
As you know, if you throw a ball gently up into the air, it rises to a certain height, then falls back down. If you throw it upward with a faster initial velocity, it reaches a higher peak before falling down.
If you shoot a bullet straight up into the air, it will rise much higher than the ball did, but eventually fall back down.
If you had a really big gun,
Illustration from Jules Verne's book From the Earth to the Moon.
could you shoot a bullet up so fast that it never came back down?
Q: Well, could you?
The answer is ... YES! Working out the details is somewhat complicated, especially if one tries to account for the air in the Earth's atmosphere: it really slows things down due to air resistance.
But in a simplified case, in which one considers only the gravitational forces on a projectile, one can work out a pretty simple solution for the escape velocity from a planet:
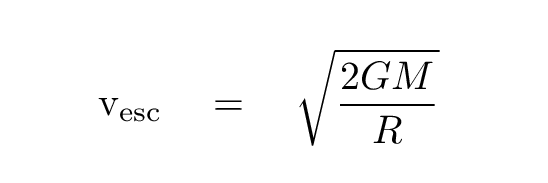
where
G = 6.67 x 10-11 N*m2/kg2
M = mass of planet (in kg)
R = radius of planet (in meters)
Let's try this out. I'll plug in the values for the Earth:
M = 5.97 x 1024 kg
R = 6378 km = 6.378 x 106 m
----> vesc = 11,200 m/s
That sounds pretty fast. That's good, actually -- we don't have to worry about accidentally jumping off the planet.
Now it's your turn.
body mass (kg) radius (km) vesc
----------------------------------------------------------------------------
Mercury 3.30 x 1023 2440
Venus 4.87 x 1024 6051
Earth 5.97 x 1024 6378
Moon 7.35 x 1022 1738
Mars 6.42 x 1023 3397
Bennu 8.0 x 1010 0.5
----------------------------------------------------------------------------
"Bennu? What's Bennu?" you may be asking. Bennu is the name of an asteroid that will soon -- in just a few months -- be visited by the spacecraft called Osiris Rex. The probe will visit the asteroid, take lots of pictures and other measurements, then touchdown briefly to grab a sample of the surface, and finally bring it all back to the Earth.
Okay. That's one factor in the "atmosphere contest" down, and one to go.
The other big factor, competing against surface gravity, are the thermal motions of the individual gas molecules. Molecules are always zipping around, bumping into each other -- and into trees and walls and the ground and other solid objects -- and bouncing off again. If one measures the speed of many molecules, one will find a rather broad distribution: some are slow, some are fast, most are somewhere in the middle.
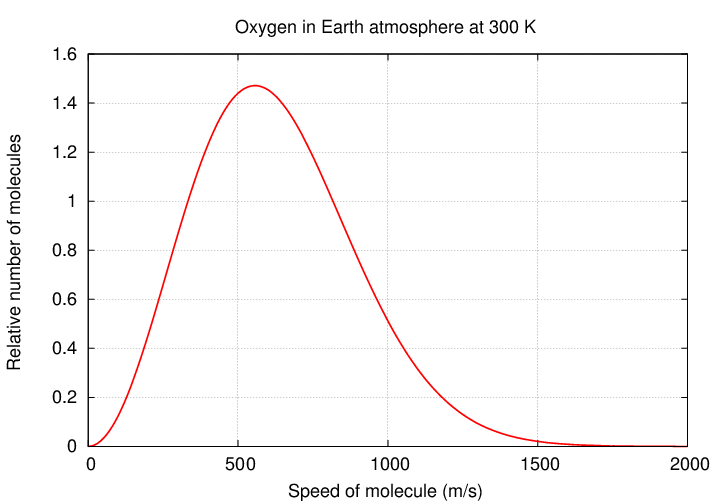
Let's pick the "typical" speed of this distribution as a way to describe the gas -- but as we will see, the fact that even a few molecules are going quite a bit faster than the "typical" one will turn out to be very important.
What controls the speed of gas molecules?
It turns out that one can estimate the "typical" speed of a molecule using the following equation:
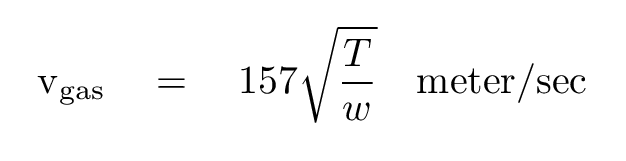
where
T = temperature of gas (Kelvin)
w = molecular weight of molecules (H = 1, H2 = 2, N2 = 28)
Fine and dandy, if we happen to know the temperature of a planet in Kelvin. Maybe you do. If you were paying attention earlier, you would have noticed the temperature of the Earth's atmosphere written down ....
Q: What is a reasonable temperature of the Earth's atmosphere?
Okay, got it. Now, let's use that temperature to calculate the typical speed for two gases in the Earth's atmosphere:
Q: What is the typical speed of H2 (= 2 hydrogen atoms) ? Q: What is the typical speed of O2 (= 2 oxygen atoms) ?
But -- what about the Moon? Or Mars? Or Venus? The temperature of those objects isn't 300 Kelvin, but we still want to know whether they ought to have an atmosphere.
Fortunately, there's a relatively simple relationship that can help you estimate the temperature of a planet in the Solar System.
Well, maybe that's too simple. Let's take it to the next mathematical level.
If one finds the point at which energy gain from the incoming sunlight exactly balances energy loss from thermal radiation, one has the equilibrium temperature of the planet. There are many places you can find a detailed formula for this quantity, but for our purposes, a VERY simplified version (assuming a perfect blackbody) is fine.
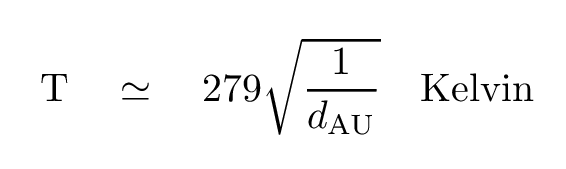
where
dAU is the distance from the Sun (in AU)
Okay, then. You now can compute the "typical" velocities of some molecules floating above the terrestrial planets, and then compare them to the escape velocities.
typical speed of
body d (AU) T (K) H2 O2 vesc
-----------------------------------------------------------------------------------
Mercury 0.39
Venus 0.72
Earth 1.0
Moon 1.0
Mars 1.52
-----------------------------------------------------------------------------------
So, do the results make sense? Does the table above explain why some planets do have atmospheres, and some planets don't?
Q: Well, does the table explain the presence of atmospheres?
Ah, yes. There is one remaining wrinkle.
The values you've calculated are the "typical" velocities of molecules in clouds of gas at each planet's temperature. Fine.
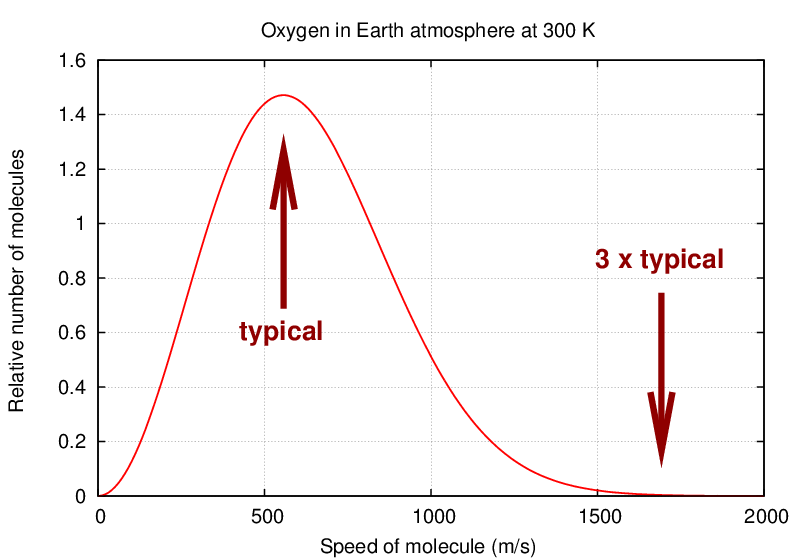
But some molecules move more slowly, and some move more quickly. Some, in fact, move MUCH more quickly. From the distribution above, you can see that the fraction of molecules moving at 3 times the "typical" speed is small ... but it is not zero.
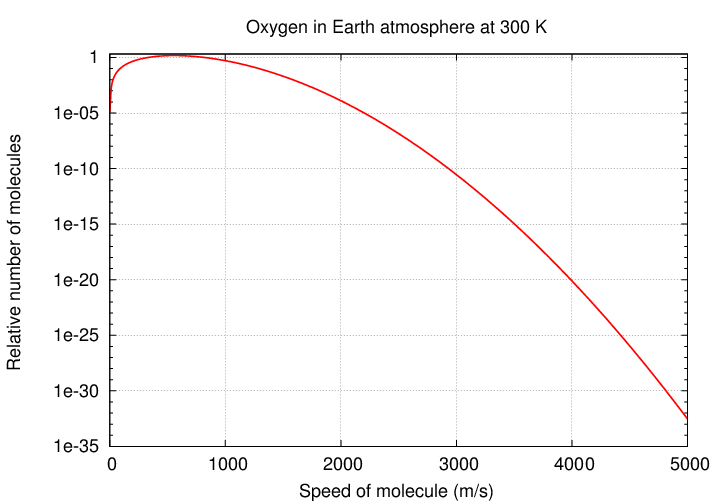
In fact, it turns out that a few molecules will be moving even faster -- at 5 times the "typical" speed, or 7 times, or maybe even 10 times. These molecules gain their speed via random collisions, and so are continually generated and removed from the population. It's all just random chance.
If those uncommonly fast molecules just happen to be near the top of the atmosphere, and if their velocities just happen to be pointing up and away from the surface, then they might fly away from the planet and never return.
Over the next few seconds (or minutes, or hours, or years), another few molecules might be bumped up to these extreme speeds, and fly away into space as well.
And then another few might fly away.
And then another few. And so on and so on and so on.
If one waits long enough, a considerable fraction of the atmosphere -- or even the entire atmosphere -- might be lost due to this sort of planetary-scale evaporation. The solar system is pretty old, around 4.5 billion years, so even very slow processes can have long-term consequences.
A good rough guide is
If escape speed is ... then .....
------------------------------------------------------------------
≤ 6 times typical speed all gas escapes
≥ 10 times typical speed no gas escapes
≥ 6 times but ≤ 10 times some gas escapes
------------------------------------------------------------------
Let's look again at that table of molecular speeds and escape speeds. Does it make sense now?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.