Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
How much energy does it take to send a spaceship far from the Earth? Let's find out. We'll use a simple model for a spaceship: a big bullet of mass M = 1 kg shot out of a big gun, like this one:
Illustration from Jules Verne's book From the Earth to the Moon.
Things get even more interesting when an adventurer from France declares that if they make the projectile hollow, he will ride inside it!
Illustration from Jules Verne's book From the Earth to the Moon.
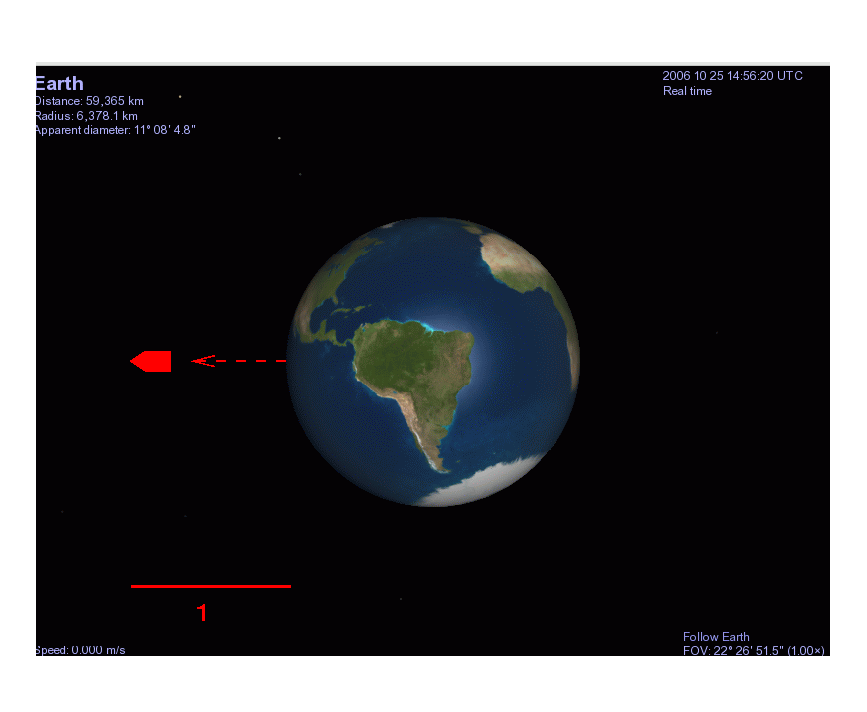
The bullet starts at the Earth's surface, a distance R1 = 6.37 x 106 meters from the center of the Earth, and then flies to a final distance of R2 = 2 x 6.37 x 106 meters, where it stops momentarily.
- How much gravitational potential energy has it gained?
- What was the bullet's kinetic energy when it left the gun?
- What was the bullet's speed when it left the gun?
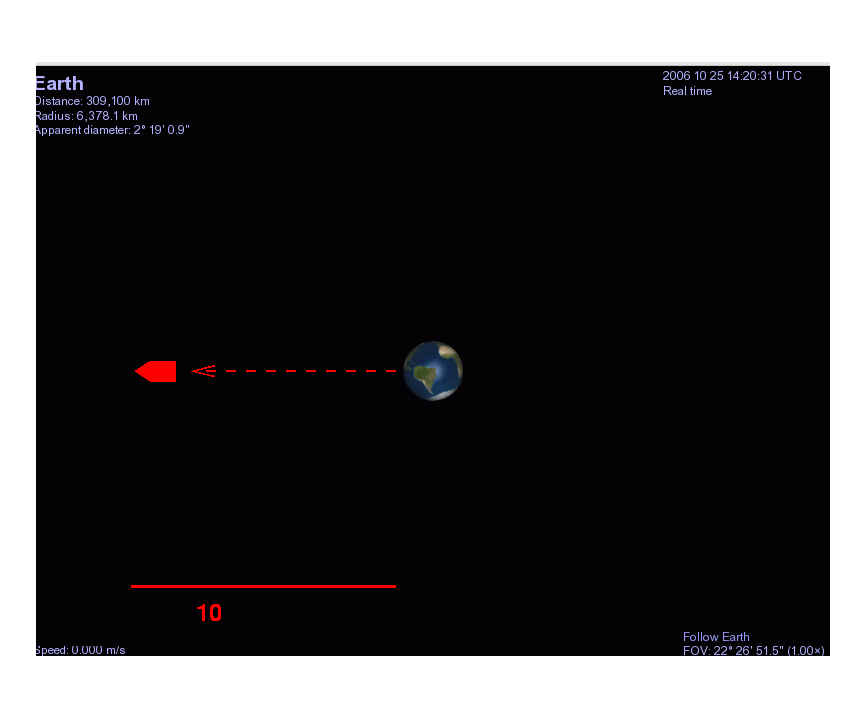
The bullet starts at the Earth's surface, a distance R1 = 6.37 x 106 meters from the center of the Earth, and then flies to a final distance of R2 = 11 x 6.37 x 106 meters, where it stops momentarily.
- How much gravitational potential energy has it gained?
- What was the bullet's kinetic energy when it left the gun?
- What was the bullet's speed when it left the gun?
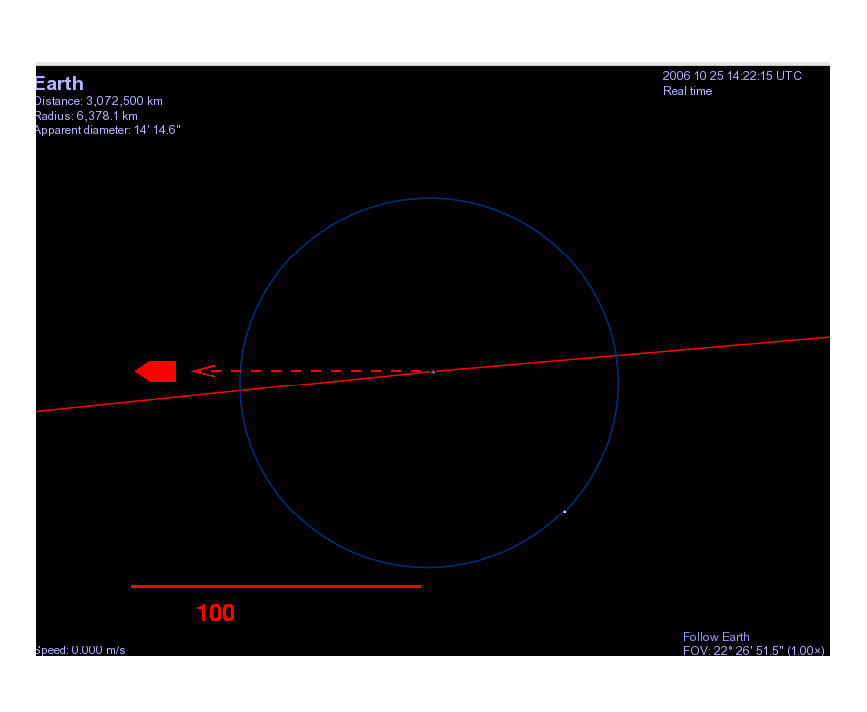
The bullet starts at the Earth's surface, a distance R1 = 6.37 x 106 meters from the center of the Earth, and then flies to a final distance of R2 = 101 x 6.37 x 106 meters, where it stops momentarily.
- How much gravitational potential energy has it gained?
- What was the bullet's kinetic energy when it left the gun?
- What was the bullet's speed when it left the gun?
(Yes, we are ignoring the effect of the Moon's gravitational force ...)
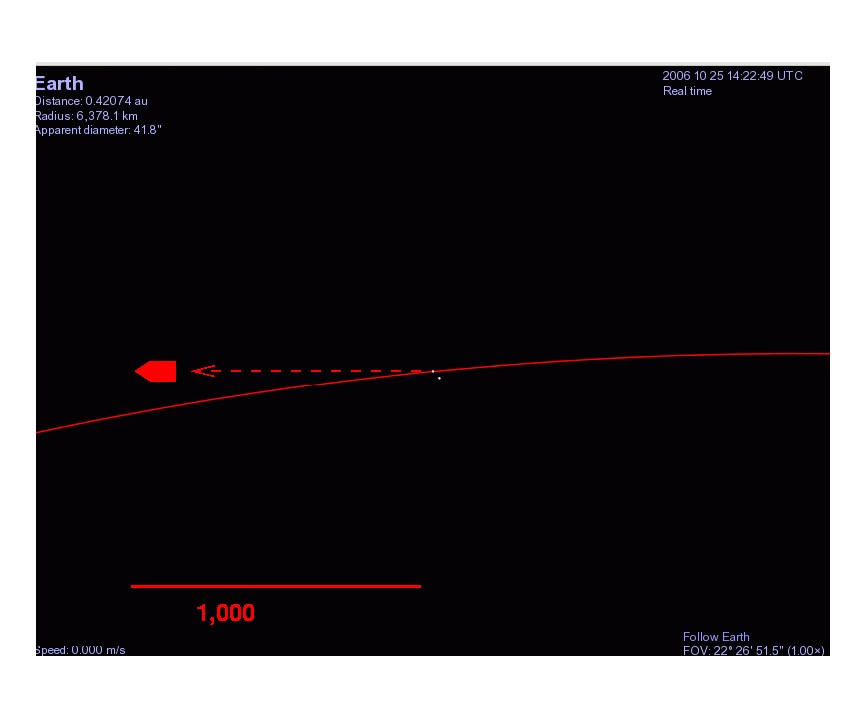
The bullet starts at the Earth's surface, a distance R1 = 6.37 x 106 meters from the center of the Earth, and then flies to a final distance of R2 = 1,001 x 6.37 x 106 meters, where it stops momentarily.
- How much gravitational potential energy has it gained?
- What was the bullet's kinetic energy when it left the gun?
- What was the bullet's speed when it left the gun?
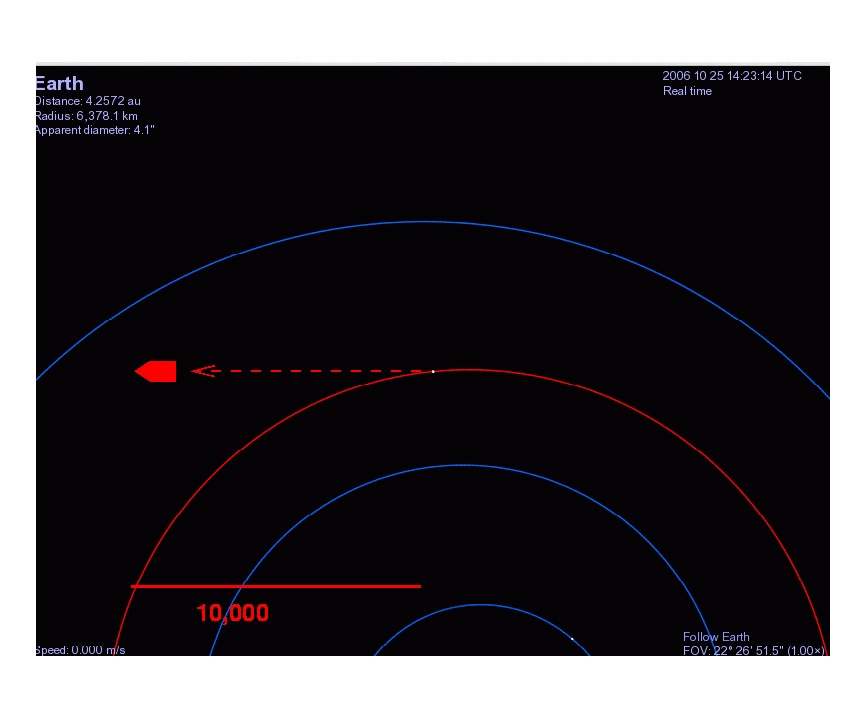
The bullet starts at the Earth's surface, a distance R1 = 6.37 x 106 meters from the center of the Earth, and then flies to a final distance of R2 = 10,001 x 6.37 x 106 meters, where it stops momentarily.
- How much gravitational potential energy has it gained?
- What was the bullet's kinetic energy when it left the gun?
- What was the bullet's speed when it left the gun?
(Yes, we are ignoring the effect of the Sun's gravitational force, and that of the other planets ....)
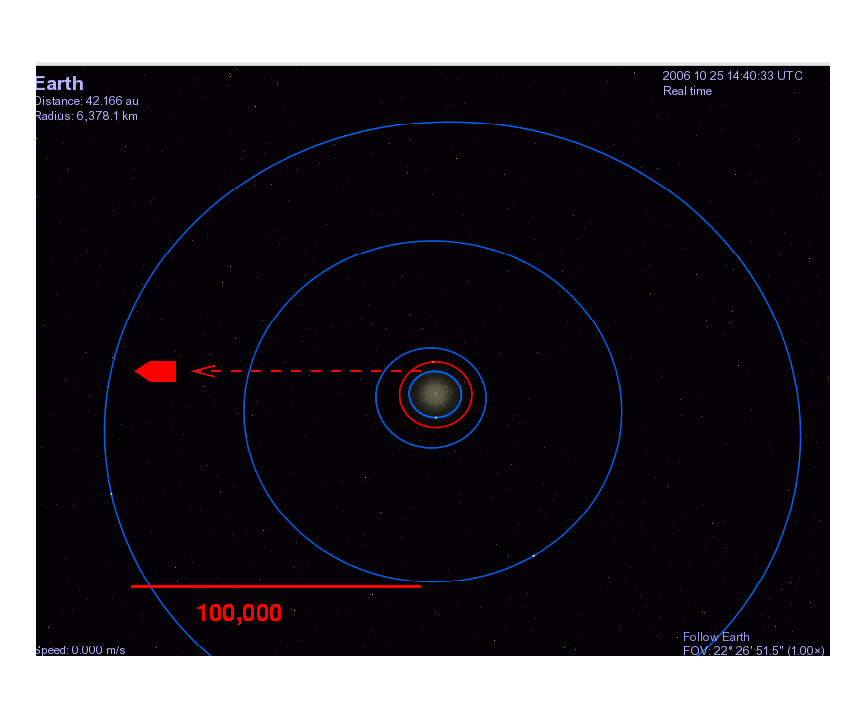
The bullet starts at the Earth's surface, a distance R1 = 6.37 x 106 meters from the center of the Earth, and then flies to a final distance of R2 = 100,001 x 6.37 x 106 meters, where it stops momentarily.
- How much gravitational potential energy has it gained?
- What was the bullet's kinetic energy when it left the gun?
- What was the bullet's speed when it left the gun?
(Yes, we are ignoring the effect of the Sun's gravitational force, and that of the other planets ....)
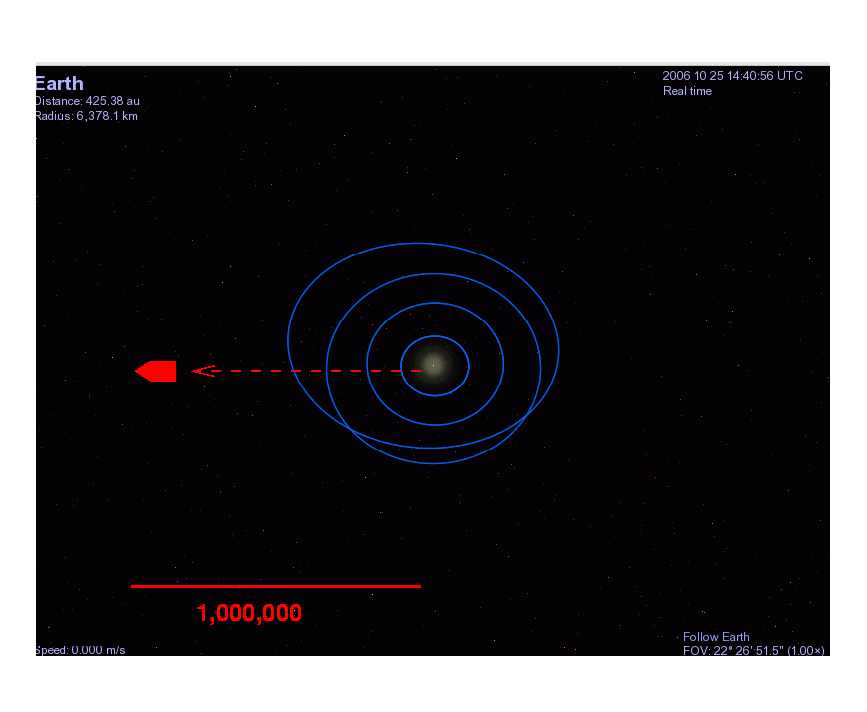
The bullet starts at the Earth's surface, a distance R1 = 6.37 x 106 meters from the center of the Earth, and then flies to a final distance of R2 = 1,000,001 x 6.37 x 106 meters, where it stops momentarily.
- How much gravitational potential energy has it gained?
- What was the bullet's kinetic energy when it left the gun?
- What was the bullet's speed when it left the gun?
(Yes, we are ignoring the effect of the Sun's gravitational force, and that of the other planets ....)
R1 (km) R2 (km) gained GPE (J) initial speed (m/s)
----------------------------------------------------------------------
6.37x10^6 2 x 6.37x10^6 31.3 million 7,913
11 x 6.37x10^6 56.9 million 10,670
101 x 6.37x10^6 62.0 million 11,135
1,001 x 6.37x10^6 62.55 million 11,185
10,001 x 6.37x10^6 62.61 million 11,190
100,001 x 6.37x10^6 62.616 million 11,190.7
1,000,001 x 6.37x10^6 62.61626 million 11,190.73
----------------------------------------------------------------------
There's a clear pattern: at some point, the bullet gains a VERY large extra distance for just a small increase in initial velocity. Suppose that we make the final distance R2 = infinity. We can use the conservation of energy to find the speed required to keep the bullet going forever:
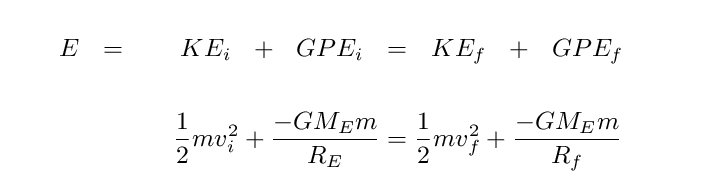
If we ask the bullet to reach a final distance Rf = ∞ with a final speed vf = 0, then
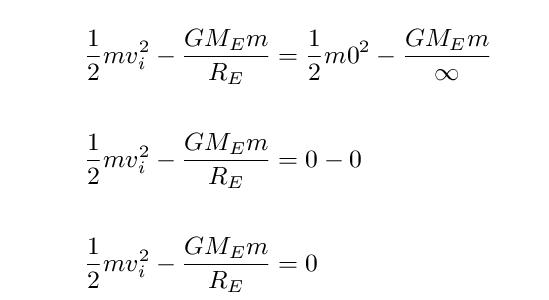
That allows us to define a special initial speed, the escape velocity from the Earth:
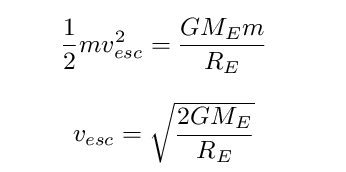
We can finish our table now ....
R1 (km) R2 (km) gained GPE (J) initial speed (m/s)
----------------------------------------------------------------------
100,001 x 6.37x10^6 62.616 million 11,190.7
1,000,001 x 6.37x10^6 62.61626 million 11,190.73
infinity 62.61633 million 11,190.74
----------------------------------------------------------------------
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.