 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
"Astrometry" is the measurement of stellar positions. In theory, if one can measure a star's position precisely -- VERY precisely, over a long period of time -- then one can detect the presence of exoplanets orbiting the star. One can even determine the properties of those exoplanets.
If we were very, very lucky, then we could observe a planet orbiting around its host star in a clear way: the system would be face on (in other words, we would be floating far above the orbital plane), and we could see clearly both the host star and the planet.

If we watched over a period of many days or weeks, the two objects would begin to revolve around the common center of mass:
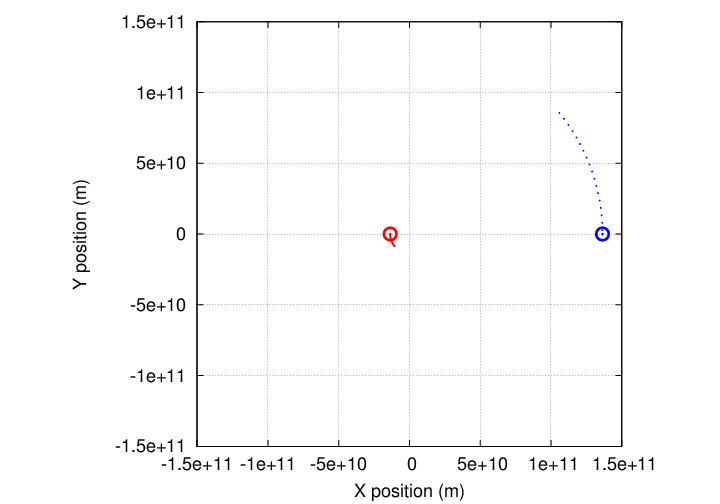
Eventually, they would complete one full orbit.
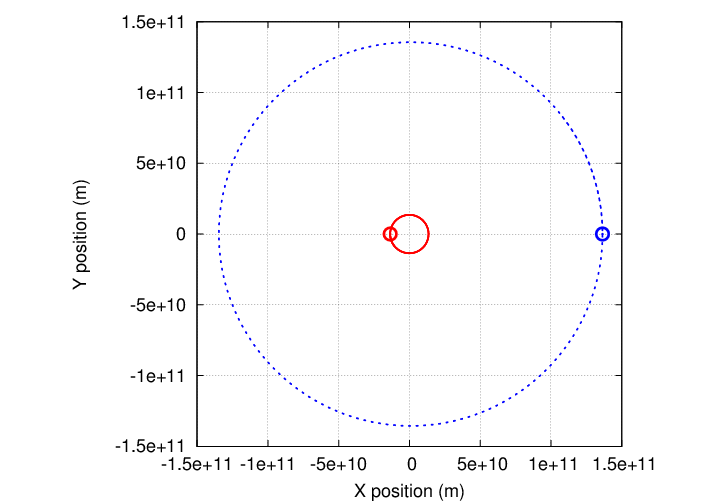
By measuring the period of this orbit, P, and the semi-major axis of the orbit, a (which is the maximum SEPARATION between the two bodies, not the distance of either from the center of mass),
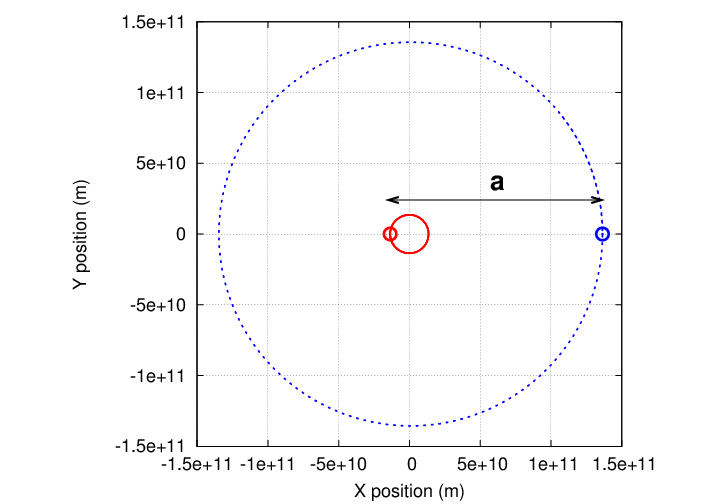
we can use Kepler's Third Law to compute the total mass of the (star + planet) together:
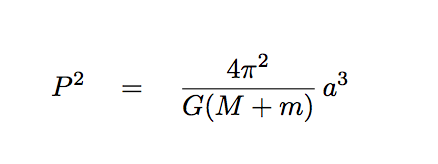
Q: Is there some way to determine the mass of the
star (M) and planet (m) individually?
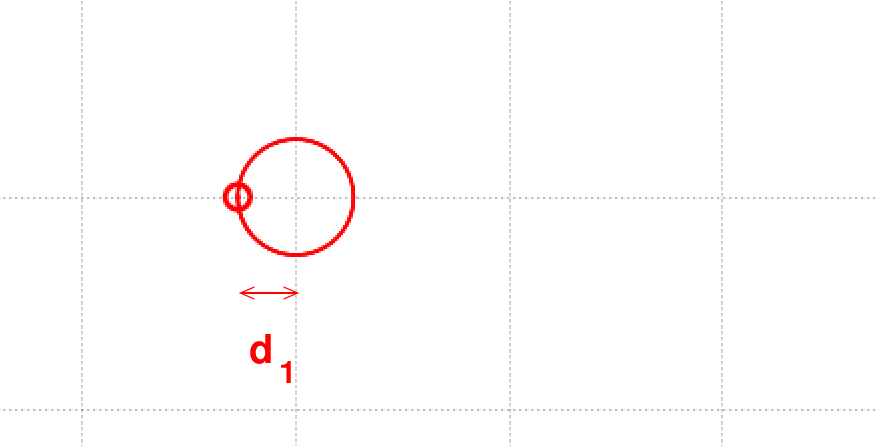
Yes! If we can see both the planet and the star, then we can easily identify the location of the center of mass -- it's the origin in the diagram below -- and the distance of each object from this center of mass.
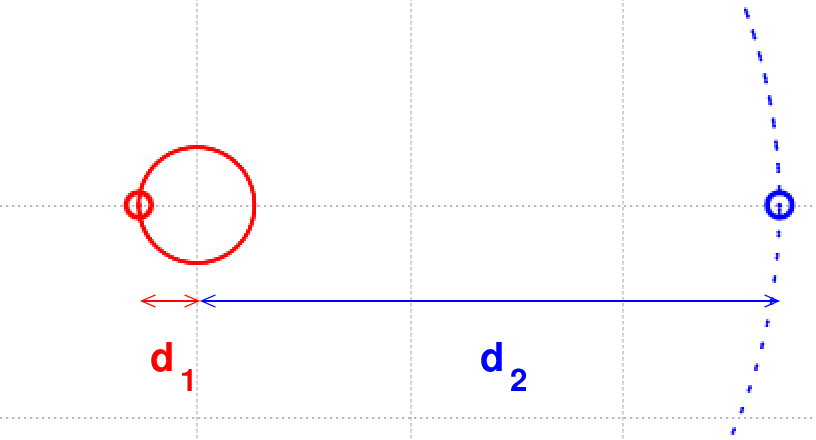
The ratio of those distances is exactly the same as (reciprocal of) the ratio of the masses:
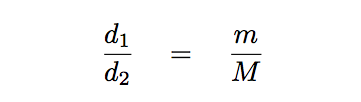
So, to recapitulate, we can observe P, a, d1, d2, and so end up with two different equations connecting the masses of star M and planet m.
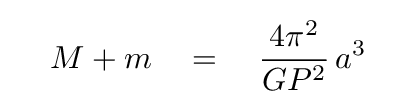
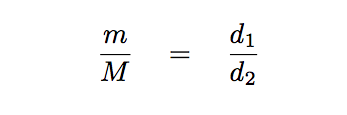
Q: Can you solve these equations to find M and m
individually?
Alas, there are many complications when we try to perform astrometry in the real world.
One of these problems is that, in most cases, the planet is too faint for us to detect; the star is so much brighter that the planet is often hidden in its glare. So, instead of seeing two objects orbiting a common center of mass, we see just one object making that journey:
It's clear that there must be another object in the system -- but is it possible to determine the mass of that object?
Q: Is it possible to determine the mass of the planet,
if we can't see it?
The answer is -- yes! As long as we can measure the following properties of the star,
then we can figure out the mass of the planet, too.
"Hey, wait a minute," you might say at this point, "how can you know the mass of the star?"That's a good point. Actually measuring the mass of a star is always a difficult task. In this case, what we often do is to use the SPECTRUM of the star to ESTIMATE its mass. That's not perfect, but it's often good enough -- maybe providing an uncertainty of only 20% or so.
Here's how to use that information to find the mass of the planet. We can define a parameter for the mass ratio of the system:
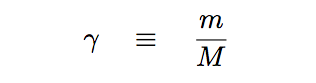
We can then re-write Kepler's Third Law using this parameter to take the place of the unknown mass of the planet.
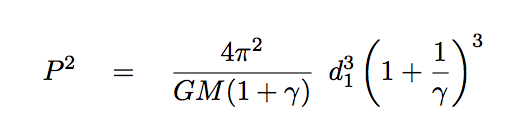
Notice that if we write things this way, there is only a single unknown variable in the equation: γ. If we re-arrange it to place the unknown quantities together, we find
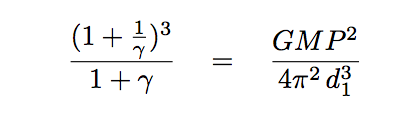
Everything on the right-hand side we can measure. The question is, can we uniquely determine a value of γ (and therefore the planet's mass) if we know the value of the right-hand side?
As long as that combination of factors on the left is single-valued over the range of 0 < γ ≤ 1, then we can find the right value of γ.
So, let's look at how that combination behaves over the range of interest:
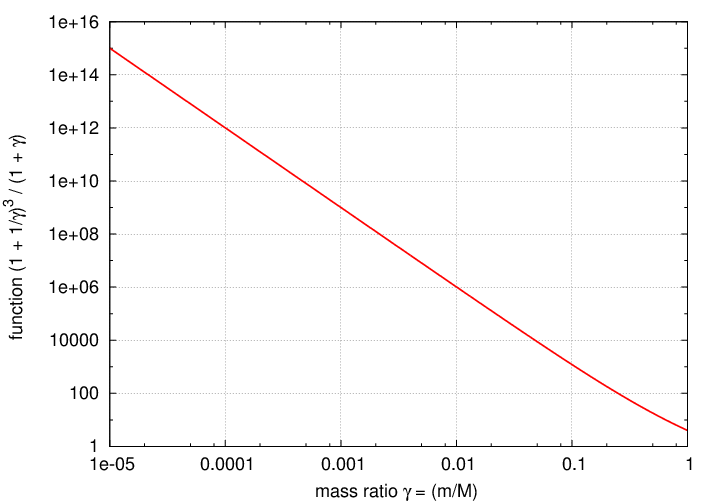
Some of you may notice that the relationship looks very linear on this log-log graph. It is easy to show that as the mass ratio decreases, the function on the Y-axis asymptotically approaches γ-3.
Hooray! As long as the mass of the planet is smaller than the mass of the star, so that γ < 1, then there is a single value of that combination of measured quantities (shown on the Y-axis) corresponding to any value of the mass ratio (shown on the X-axis). So, finding the mass of the planet sounds pretty easy:
So, the bottom line is, as long as we can measure the orbital reflex motion of the star around the center of mass, we can still determine the mass of the (unseen) planet.
Alas, the motion of a star around the center-of-mass of the star-planet system is just ONE of the motions we see when we look closely at a star in the sky. There are (at least) two others which are typically much, much larger than the orbital motion we seek.
For example, let's look at one particular star, not too far away from the Sun. The Hipparcos satellite measured its position VERY precisely over a three-year period.
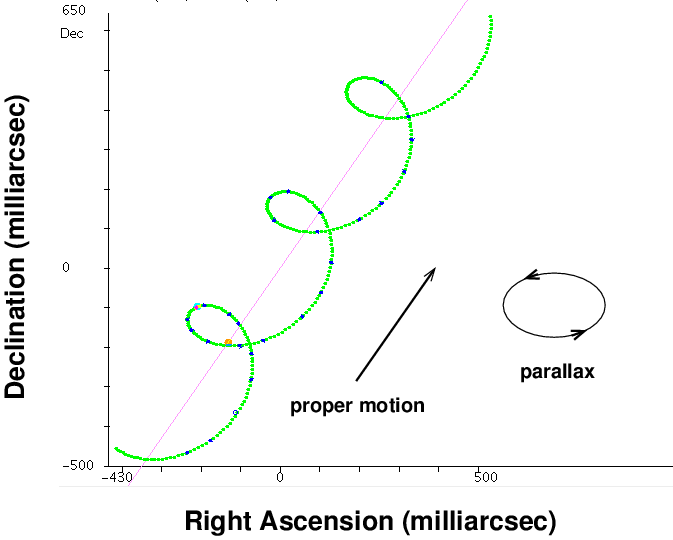
Image thanks to the terrific tools available at
the ESA Hipparcos Tools website
This "spiral in space" is a combination of a linear motion (that's the proper motion, from lower-left to upper-right) and a periodic ellipsoidal variation (that's the parallax).
Q: Use this graph to determine the proper motion
of this star (milli-arcsec per year).
Use this graph to determine the parallax
of this star (milli-arcsec).
What is the distance to this star?
BONUS! What star is this?
So, if we add together all three motions of the star -- proper motion, parallax, and its revolution around its center of mass with the planet -- we see a rather complicated path across the sky. In the figure below,
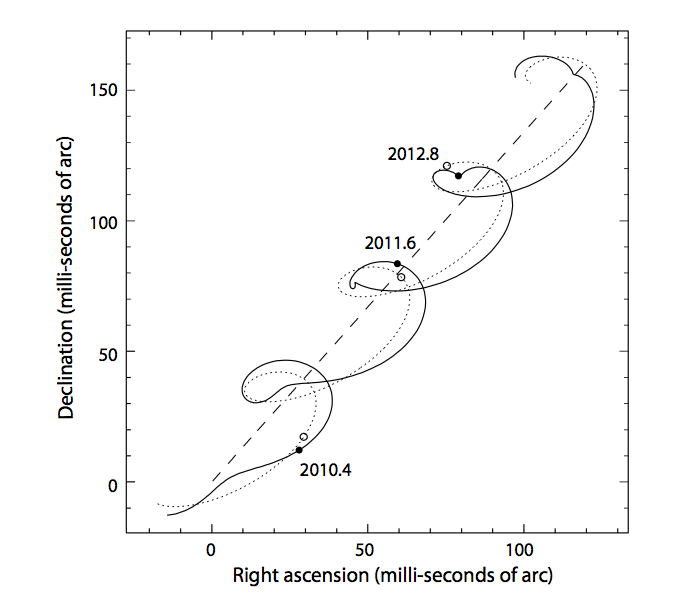
Figure 2 taken from
Perryman (European Physical Journal H, 37, 745 (2012))
Clearly, we must do a VERY good job of fitting and removing the proper motion and parallax in order to have any chance of using the tiny residual to compute the orbital motion of the star.
As you may recall, one of the drawbacks of the radial velocity method is that it can only yield a lower limit on the mass of an unseen planet. The reason is the effect of the inclination of a planetary (and stellar) orbit. Radial velocity measurements can give us information on only one component of the host star's motion, and so any planetary mass derived solely from radial velocity will suffer from ambiguity:
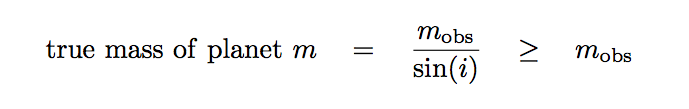
Q: How many components of motion must we observe
in order to derive the true mass of a planet?
The answer, it turns out, is set by the nature of the gravitational force and and space in which we live. Any simple (non-relativistic) two-body system will feature orbits which lie in a two-dimensional plane.
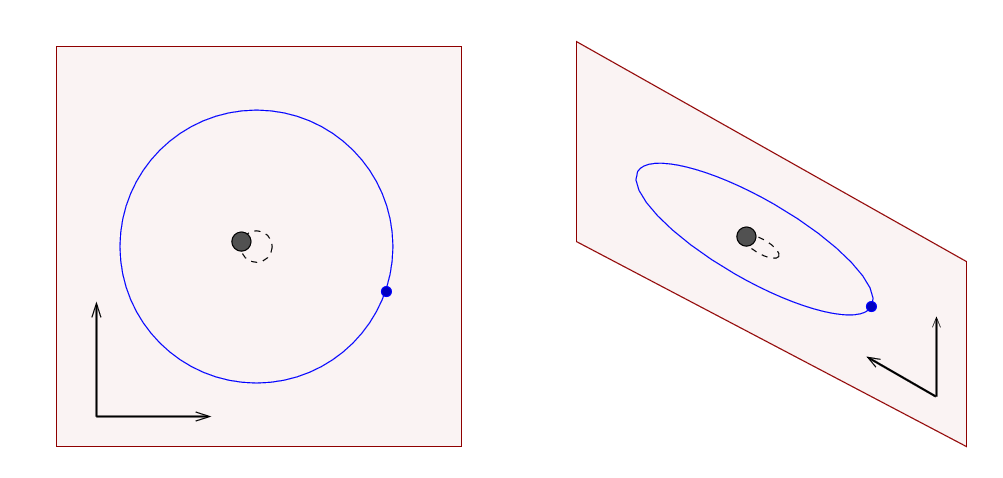
So, as long as we can measure properly two components of the motion of (at least one) of these bodies, we have a chance to figure out all the masses and velocities and other properties.
Yes, yes, we need additional information: the distance to the system.
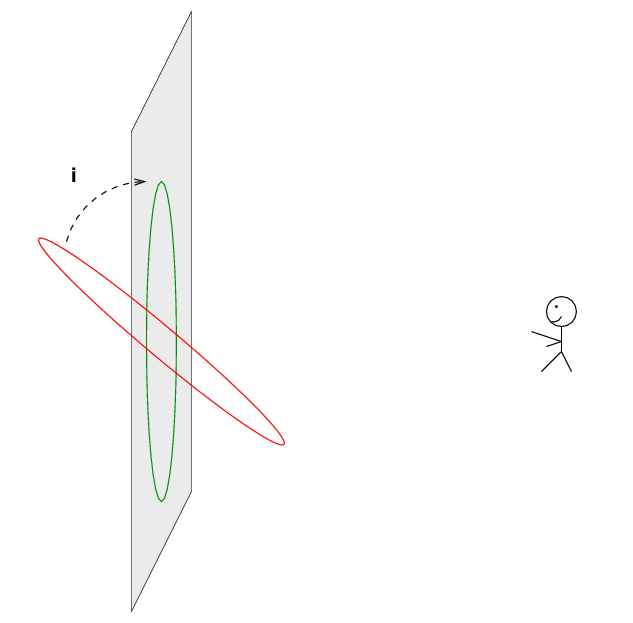
But -- how can we be sure that we know the inclination of the orbit? All two-body orbits are ellipses, and what happens when one tilts an ellipse?
Well, you probably know that if you tilt a CIRCLE, you get an ellipse:
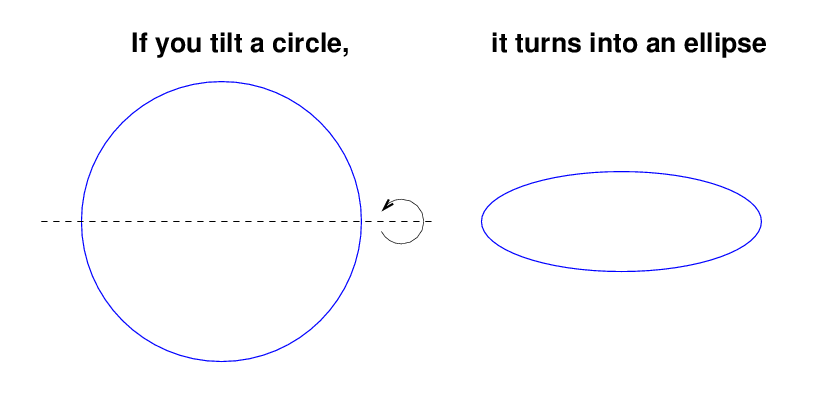
But don't forget that if you tilt an ellipse just the right way, you can also end up with a circle:
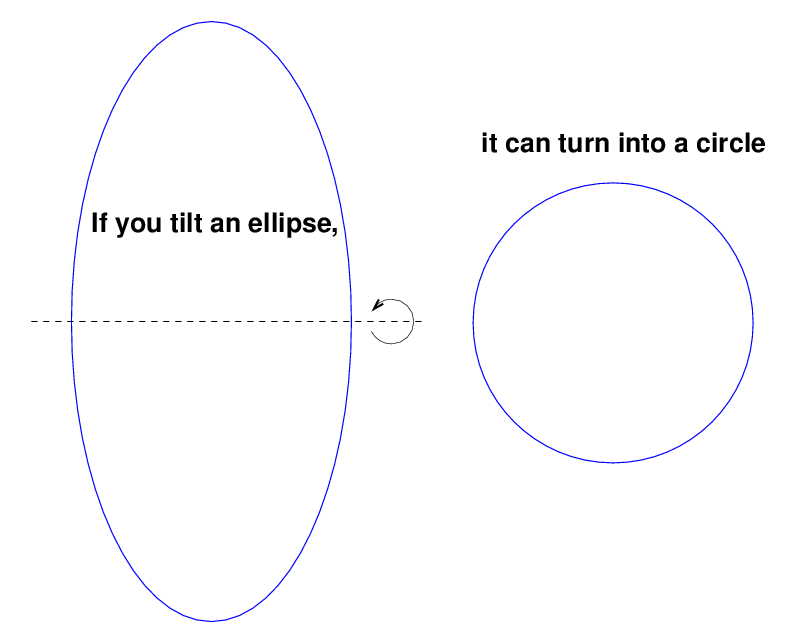
In the general case, tilting one ellipse will yield an ellipse of a different shape.
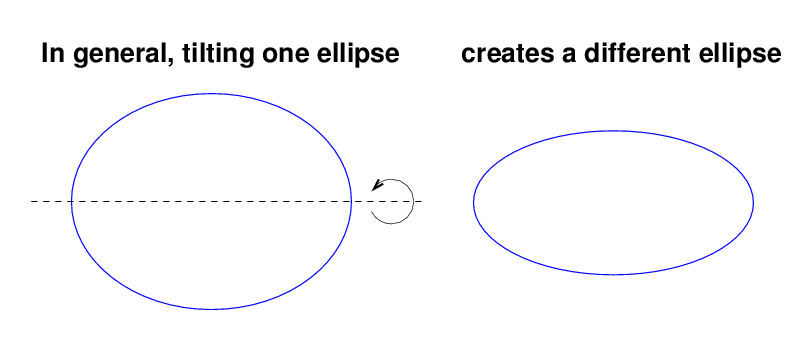
Q: So, how can we tell which ellipse is the RIGHT ellipse?
In other words, what is the secret to figuring out the
inclination of the orbit?
The secret is ... TIME. At least, that's one way to put it.
Let me explain. If I show you a picture of two orbits drawn with a continuous line, it's hard to see the difference that TIME makes. But if I show you a picture with the position of the one body measured at regular, equal time intervals -- for example, once every day -- then suddenly you can see the difference.
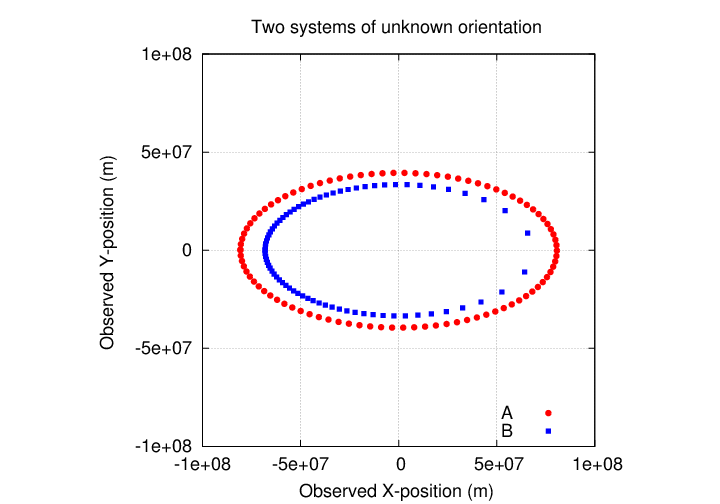
You can see that the star in system A moves with an angular speed which does vary -- it appears to move faster when near X=0 than when Y=0 -- but that variation is symmetric. The star in system B appears to change speeds in an ASYMMETRIC manner: it moves much more quickly at the right side of of its orbit than the left side.
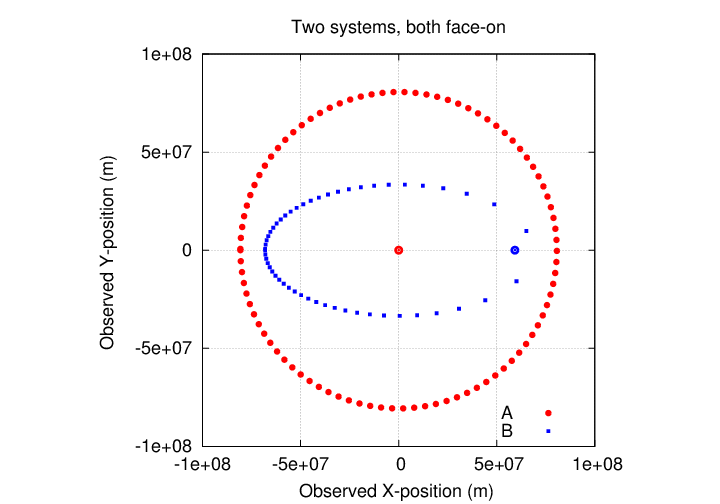
In the figure below, I've placed both orbits into a face-on orientation; the B system was face-on to start, but the A system was inclined by about 30 degrees in the figure above. In addition, I've placed a big dot to mark the center of mass for each system. In the case of A, the star we observe is moving in a circular path around this center of mass; but in the case of B, the center of mass is much closer to the right-hand side of the orbit.
It turns out that this sort of variation in the speed of the one visible object can give us all the information we need to figure out the unknown inclination, correct for its effect, and thus determine the mass of the invisible body. We just need to remember the First and Second Laws of a certain Johannes Kepler:
Here's how we do it. Start with the observed motion of a host star due to its orbit around the center of mass with an invisible companion.
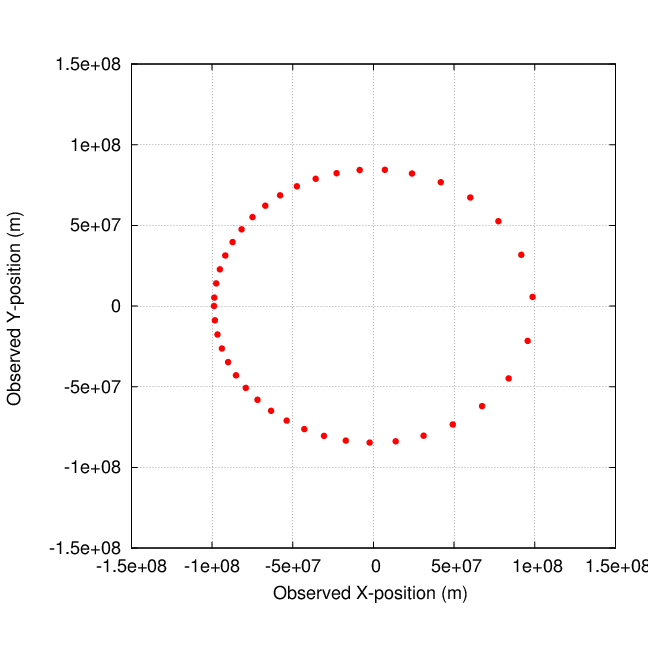
Determine the semi-major axis, a, and semi-minor axis, b.
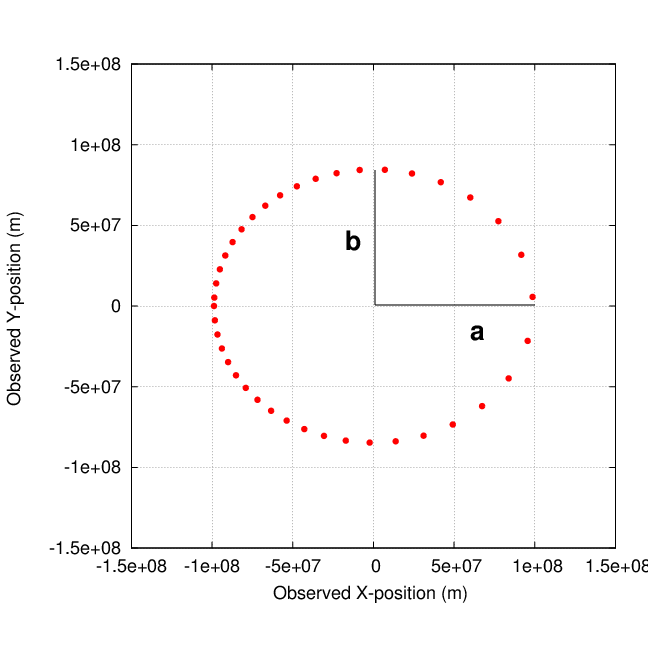
The eccentricity e of an ellipse can be calculated via
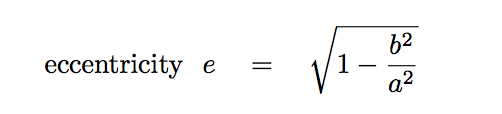
Now we can mark the locations of the two foci of this ellipse: the distance f from the center to each focus is simply
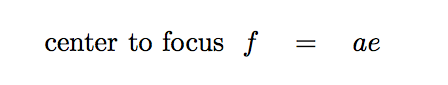
Kepler's First Law implies that the center of mass of this system is located at one of these two foci -- but which one?
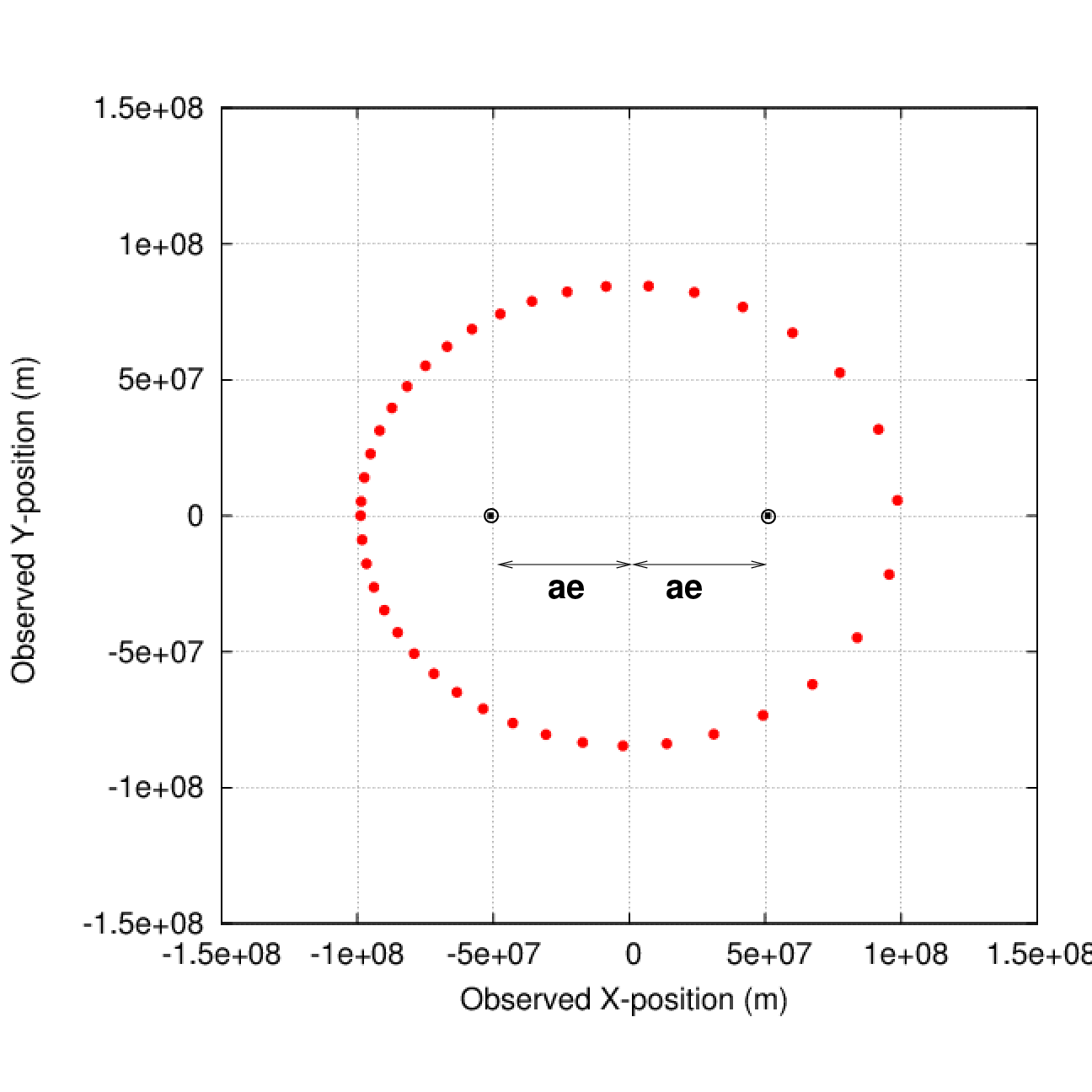
Q: Which focus marks the center of mass?
According to Kepler's Second Law, a line drawn from the focus containing the center of mass to the location of the visible star should sweep out equal areas in equal periods of time. There are only two choices -- so let's try them both and see if either one works.
Pick the left-hand focus, draw radius vectors at equal intervals of time, and measure the areas of the resulting triangles.
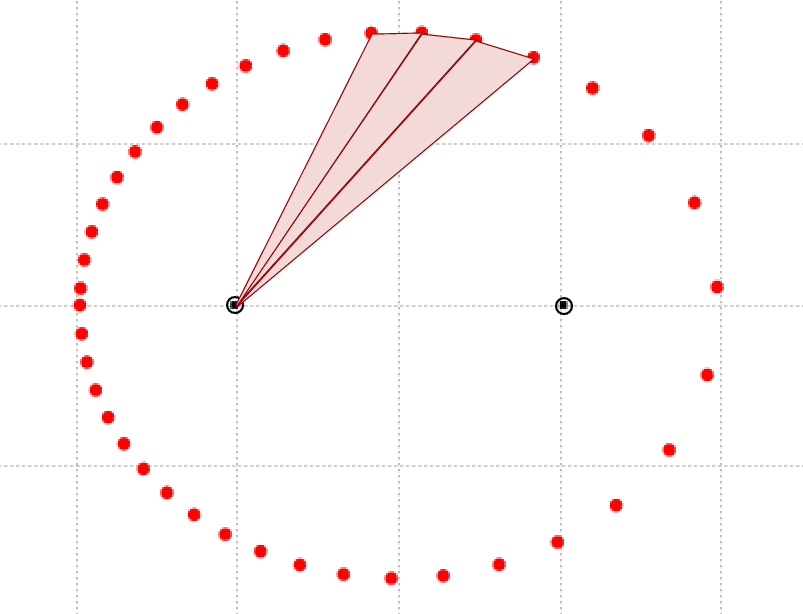
Repeat this process for the right-hand focus:
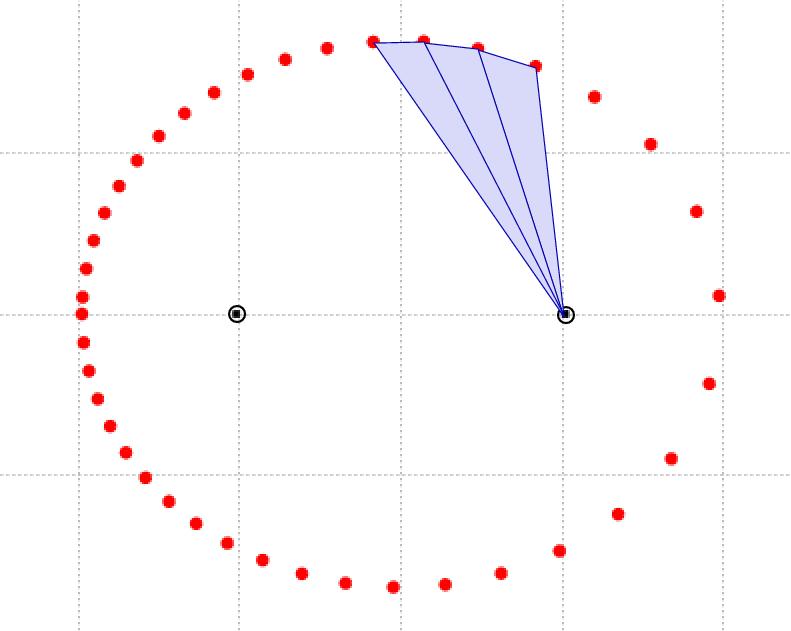
Now, simply examine the areas of all those little triangles over the course of the entire orbit.
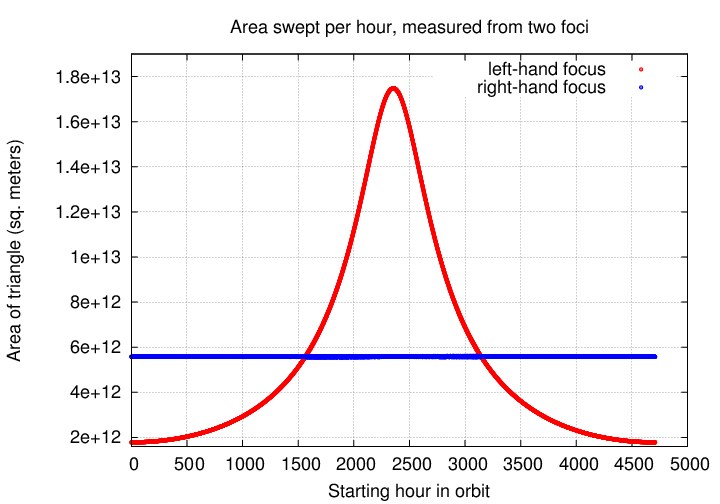
In this case, the right-hand focus marked the true position of the center of mass of the system.
"What a minute," you might interject at this point, "what about inclination? This section is supposed to tell us how to deal with the inclination of an orbit!"
You're right. Let's look at the effects of inclination, now that we understand how Kepler's Laws can be used to investigate elliptical orbits.
Suppose that we observe the orbit of a host star around the center of mass of its system, and so infer that there must be an unseen planet.
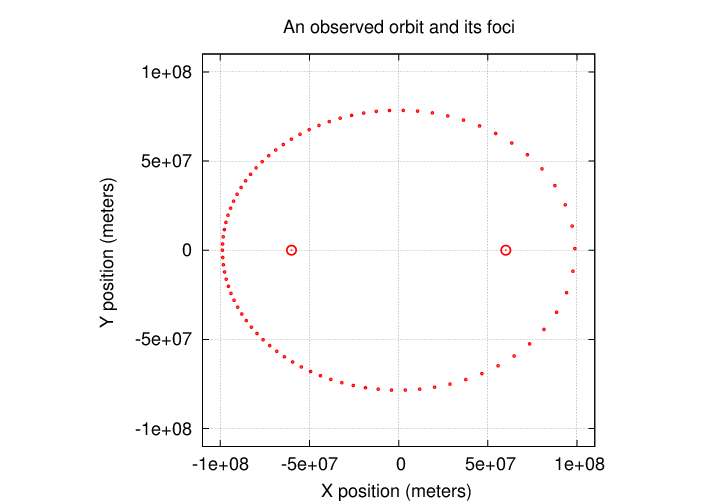
We go through all the usual steps -- figuring out the ellipticity of the orbit, locating the foci, and computing the area swept out for each focus -- but end up with an unsatisfying result:
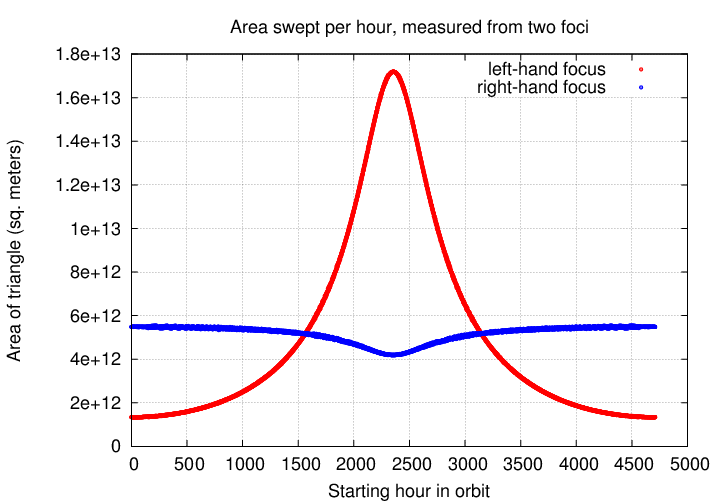
The right-hand focus is certainly BETTER than the left-hand focus, but the area swept out over the course of the orbit is not constant; it changes by about 20 percent.
This is a signal that we are observing the orbit at some inclination, rather than face-on. What we have to do is to de-project the observed positions onto a properly face-on plane in order to correct them. But what is the actual angle of inclination?
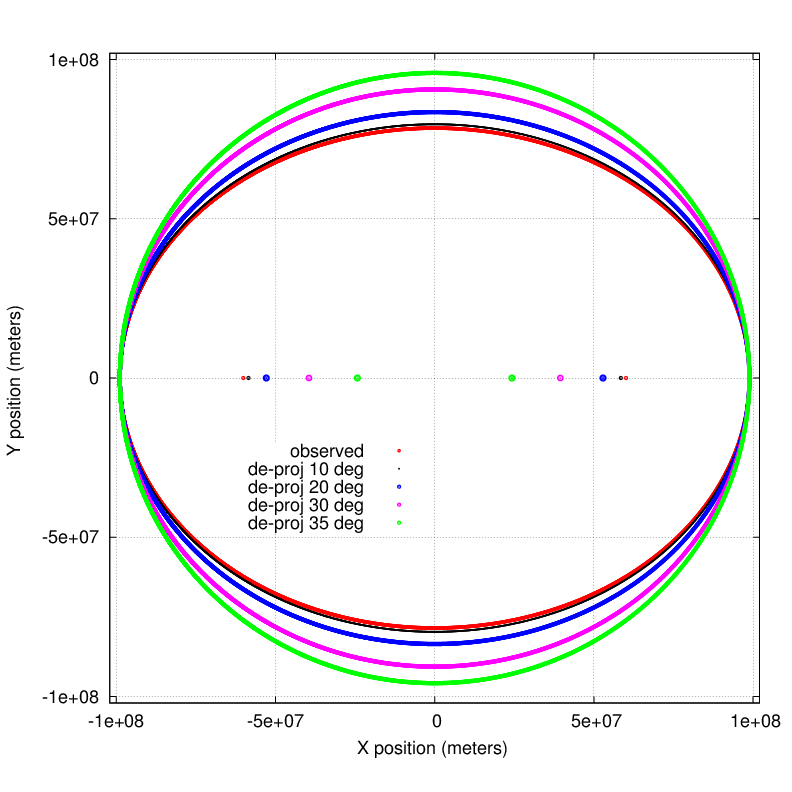
We don't know -- but we can find out with a bit of trial and error. Let's de-project the observations by a range of possible angles, and compute the foci for each case.
Then, for each possible angle, we apply Kepler's Second Law to see how the area swept out by the star changes over the course of its orbit.
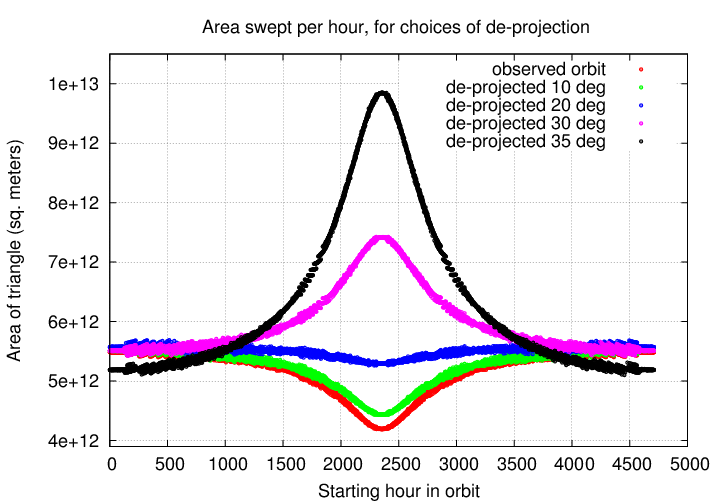
Looking at the graph, the best choice for inclination angle is 20 degrees; but there is still a bit of variation in the area swept out. Fortunately, computers are good at repeating tasks over and over, and don't mind trying lots and lots of possible inclination angles. They can figure out the best one for us.
So, THAT'S how we can determine the inclination of an orbit using astrometry, even if we can see only the host star as it moves.
Sharp-eyed readers may have noticed that all the examples in this section involve orbits which are projected around their major axes. In the real world, some orbits will be projected around lines which do not run along their major (or minor) axis.But, again, we can use computers to check for these situations: look for projections around lines which run in every possible direction, and pick the one which yields the most-constant areal velocity for the star.
Going through all the details would take more time and space than I have here ...
The final reason that very few planets have been discovered so far by astrometric techniques is that the observable reflex motions of their host stars are, typically, very, very, VERY small.
How small? Let's use Jupiter and the Sun as an example.
Q: You observe a stellar system in which a planet identical
to Jupiter orbits a star identical to the Sun.
The system is at a distance of d = 10 pc.
If the planet orbits at Jupiter's distance,
what is the semi-major axis of the star's reflex motion?
Express your answer in milli-arcseconds.
What if the planet has an orbit like the Earth's,
with an orbital radius of 1 AU?
We can make a simple table summarizing the results:
| dist to system | R = 0.1 AU | R = 1 AU | R = 10 AU | R = 100 AU |
| 1 pc | 0.1 mas | 1 mas | 10 mas | 100 mas |
| 10 pc | 0.01 mas | 0.1 mas | 1 mas | 10 mas |
| 100 pc | 0.001 mas | 0.01 mas | 0.1 mas | 1 mas |
The best astrometric measurements before Gaia had a precision of about 1 mas:
I've marked elements of the table above with expected astrometric motions of at least 1 mas in a light blue background.
There are plenty of stars within a distance of 100 pc -- so why did astronomers not detect any planets around these stars via astrometry?
Q: What is the orbital period of a planet orbiting a
Sun-like star at 1 AU?
What is the orbital period of a planet orbiting a
Sun-like star at 10 AU?
Q: How long did the Hipparcos satellite operate in orbit?
So, clearly, the Hipparcos satellite didn't observe stars for a period long enough to measure the orbits of stars around their centers-of-mass with many planets. Let's find out just how limited Hipparcos would be as a astrometric-planet-discovering instrument.
Imagine a Jupiter-mass object circling a Sun-like star.
Q: What is the maximum orbital radius corresponding
to an orbit of P = 4 years?
Q: What would be the maximum radius of the star's orbit
around the center-of-mass with such a planet?
Q: What would be the maximum distance from the Sun
at which Hipparcos could detect such an orbit?
Okay, good. You have two limits here: a maximum period (4 years), and a maximum distance from the Sun (which you just computed) at which such an astrometric signal could be measured by Hipparcos.
Q: In the NASA Extragalactic Database table,
how many planets have been found satisfying these constraints?
Not many ...
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.