 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So, if you have an echelle spectrograph, and a big telescope which collects lots of photons, it should be pretty easy to detect motions of a star of less than 10 m/s, right?
Wrong.
There are many inconvenient truths that we have ignored up to this point. For example, humans live on the Earth. This causes problems in a number of different ways:
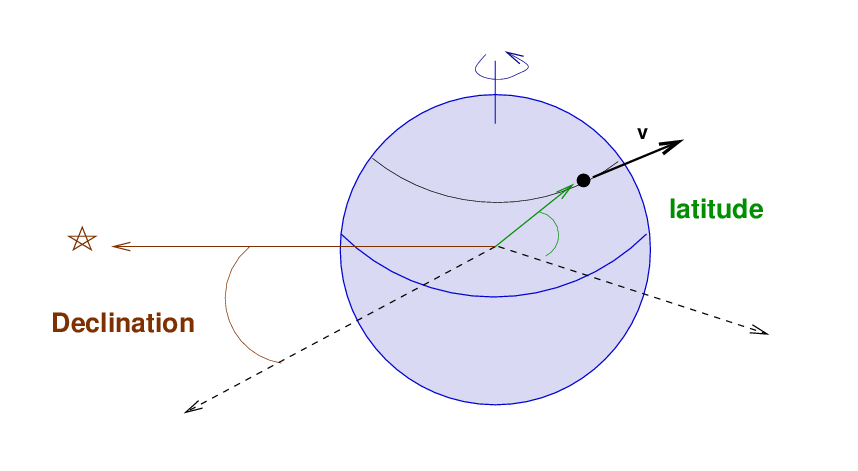
Let's continue to ignore the first couple of items, but look more closely at the final two. As we look at a star from a ground-based observatory, our telescope is carried along with the Earth's surface. The radial velocity of the telescope, relative to the star, depends on two items:

Q: What is the speed of the observatory v?
Q: What is the maximum possible component of that
speed in the direction of the star?
Q: Can you come up with a single equation for the
radial velocity of the observatory, as seen
by the star? What are the input parameters
to this equation?
Of course, the Earth is also revolving in orbit around the Sun, and that motion, too, must be taken into account -- very, very carefully. Even small mistakes can turn out to be significant.
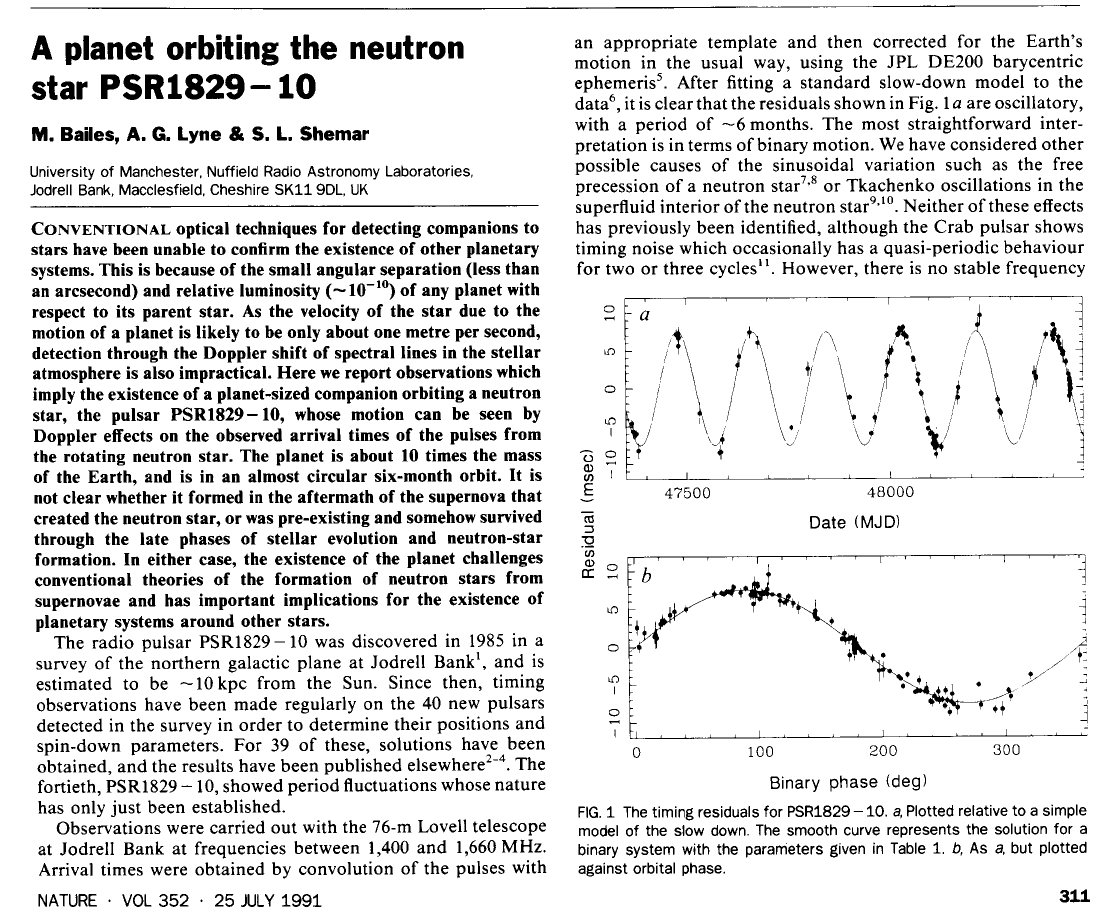
Taken from
Bailes, Lyne and Shemar, Nature 352, 311 (1991)
Less than a year later, as the New York Times reported, Lyne retracted this discovery at the January, 1992, meeting of the American Astronomical Society. You can read a short extract about the event in Strange New Worlds: The Search for Alien Planets and Life Beyond Our Solar System by Ray Jayawardhana, or another short extract taken from Pluto Confidential by Lawrence Marschall and Stephan Maran.

Taken from
Lyne and Bailes, Nature 355, 213L (1992)
So, we don't want to make a similar mistake. How can we compute the radial velocity component of the Earth's motion around the Sun?
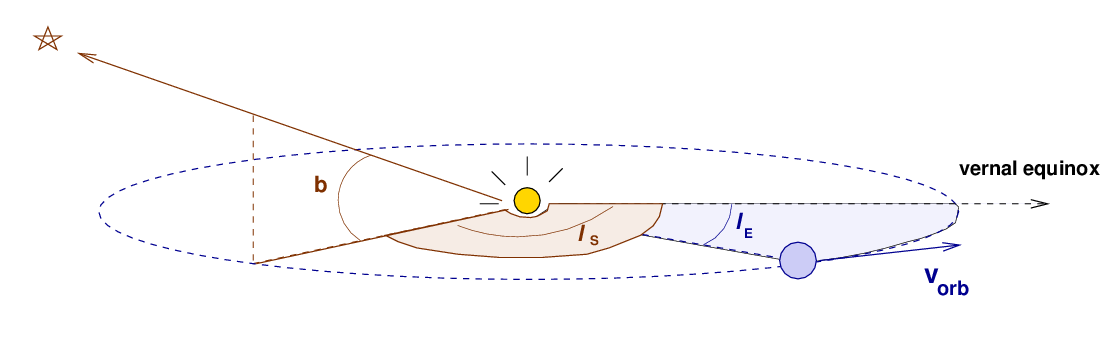
Q: What is the speed of the Earth vorb?
Q: What is the maximum possible component of that
speed in the direction of the star?
Q: Can you come up with a single equation for the
radial velocity of the Earth, as seen
by the star? What are the input parameters
to this equation?
The effect of the Earth's spin alone is important on short timescales -- within a single night, or over several nights.
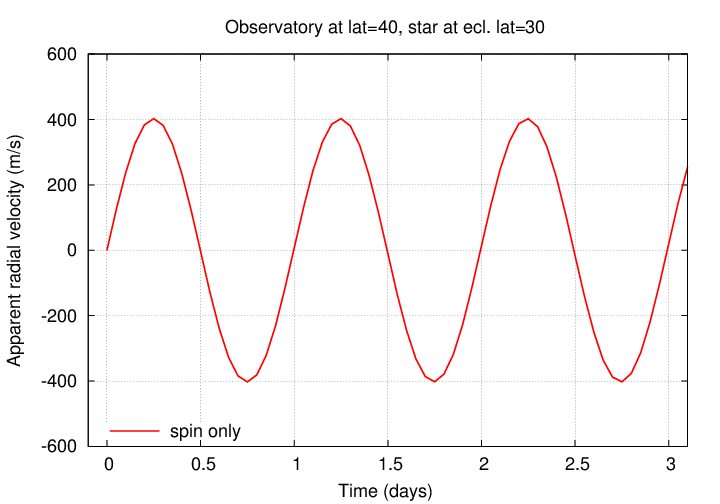
But the effect of the Earth's orbital motion is also important, even over a few days,
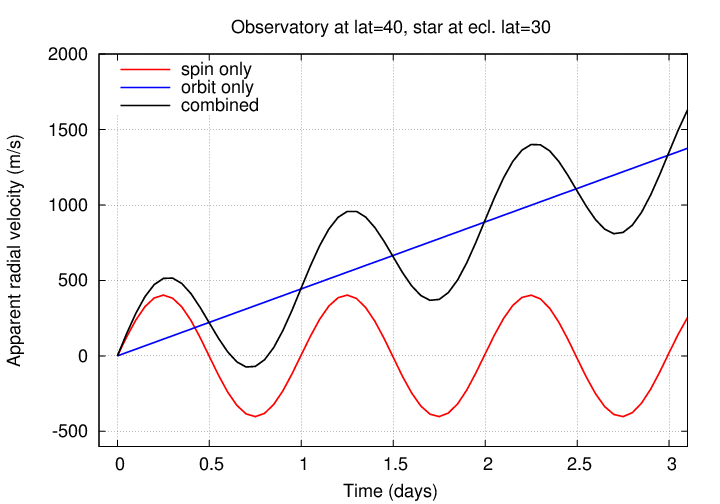
... and ESPECIALLY over longer periods:
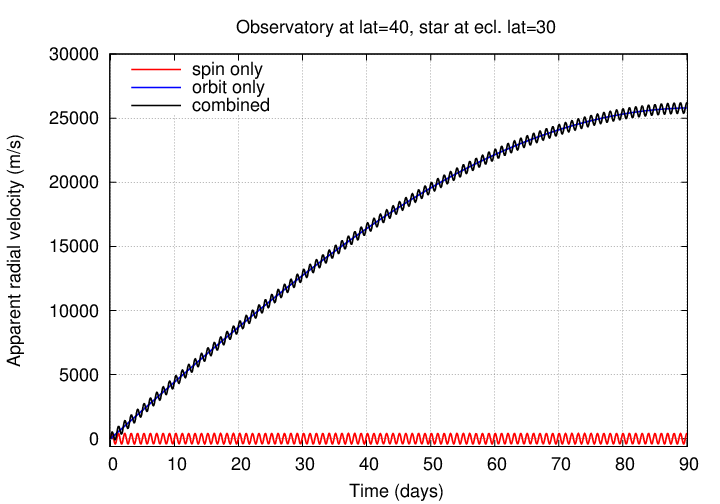
Okay, you've figured out how to keep your spectrograph stable. You have a good scheme for calibrating the data. You correctly account for the motion of the Earth around the Sun, and your telescope around the axis of the Earth. The signal you deduce consists solely and precisely of the light which was emitted by the star.
That means that every feature you see in the radial velocity must be due to reflex motion, right?
WRONG!
The problem is that stars aren't perfectly quiet sources of light. They have their own sources of variation in intensity and in wavelength which can compete with or even overwhelm changes caused by a planet.
Consider the star we know best: the Sun.

See all those little spots? They are somewhat cooler than the surroundings -- maybe 4000 K rather than 5800 K -- and so they emit less light. What effect will they have on the Sun's radial velocity?
The radius of the Sun is about 7 x 108 meters.
Its period of rotation is very roughly 30 days (but depends
on solar latitude).
Q: What is the rotational speed of the gas moving
around the Sun's equator?
Q: What fraction of the Sun's left half (which is coming
toward us) in the picture above is covered by sunspots?
Q: Estimate very roughly how much the overall radial
velocity of the Sun changes due to these spots.
Let's compare your results to a more sophisticated calculation by a recent study: Korhonen et al. (2015) look at a solar-like star with a spot of radius of about 5 degrees on the solar photosphere. In the figure below, panel "b)" shows the variations in radial velocity of the star, as seen by a distant observer. (Panels "c)" and "d)" show the signal of a Neptune-mass planet in a 25-day orbit, without and with the sunspot).
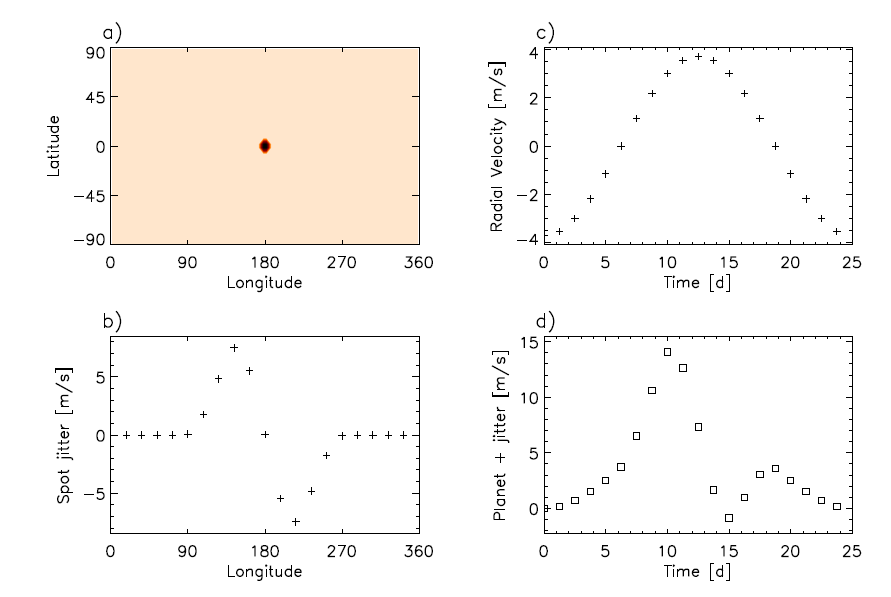
Fig 1 from
Korhonen et al., MNRAS accepted (2015)
The calculation above features just one big spot, which is sort of a worst case scenario. If there are many spots, they might act to cancel each other out. Let's see ....
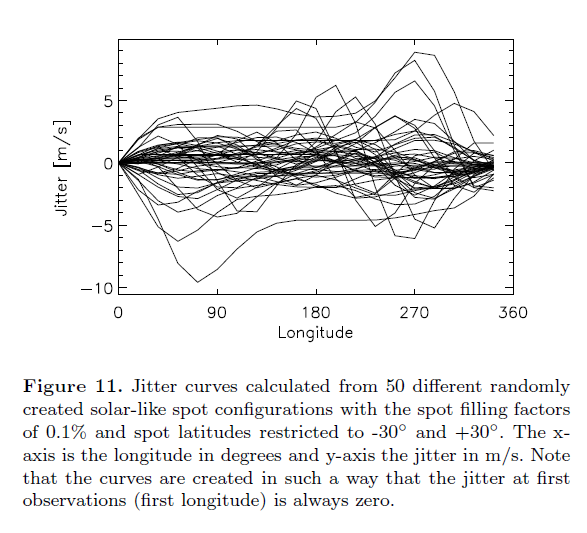
Fig 11 from
Korhonen et al., MNRAS accepted (2015)
Of course, this effect depends on several factors: the rotational speed of the star and the inclination of its rotational axis to the line of sight, in particular. Observing at longer wavelengths (farther into the red and IR) can reduce the jitter, as the contrast in brightness between the spot and its surroundings will be lower.
Solar-type stars may have cycles of stellar activity, during which the number of spots would increase. Clearly, the more activity, the larger the "jitter" in the measured radial velocity.
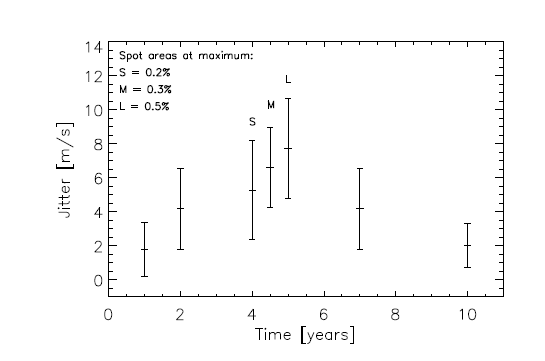
Fig 16 from
Korhonen et al., MNRAS accepted (2015)
Planet hunters must hope that they look for their targets during the right point in a star's cycle.
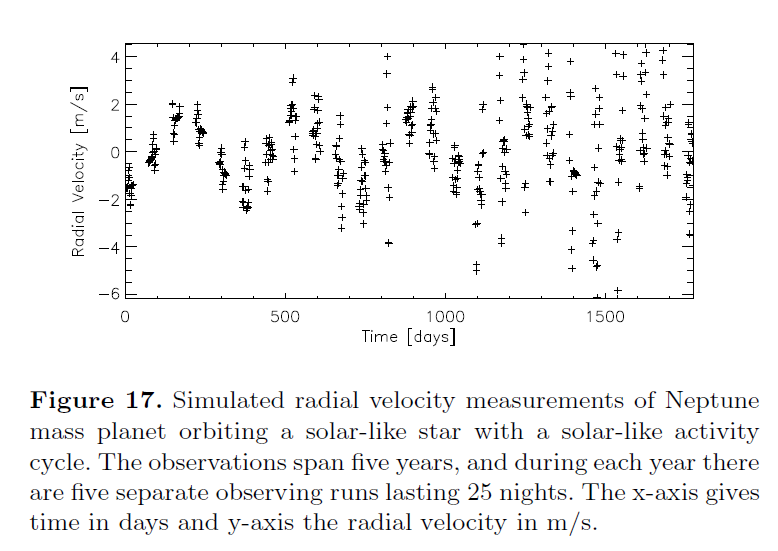
Fig 16 from
Korhonen et al., MNRAS accepted (2015)
Suppose that you've managed to avoid stars with spots and strong stellar activity cycles. Can you be sure that your spectra will yield measurements with a precision of 1 m/s?
Maybe, maybe not. Consider the following four stars.
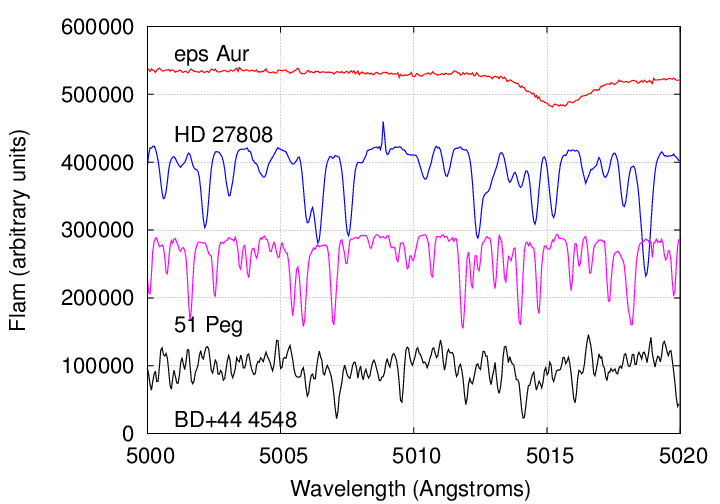
Data courtesy of the
Elodie archive
Q: Which of these stars would yield the
most precise radial velocities? Why?
Q: What's the reason for these differences?
Perhaps these labels will provide a clue.
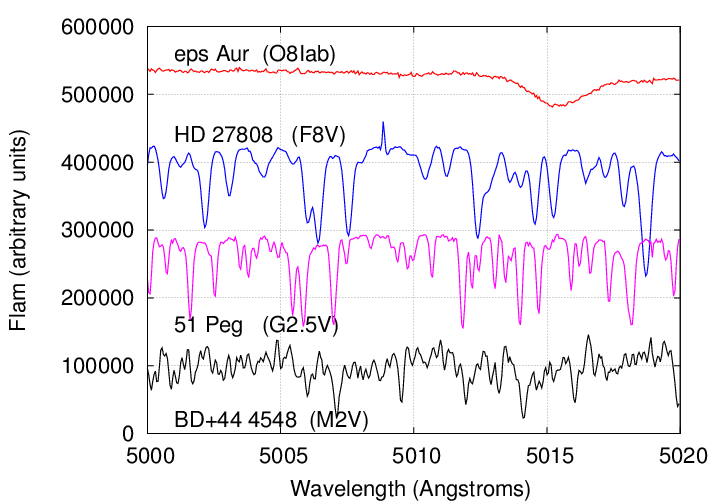
Data courtesy of the
Elodie archive
Yes, the spectral class of a star -- which depends largely on the temperature of the photosphere, and on the pressure to a lesser degree -- plays a large role in the nature of the absorption lines in a spectrum.
The "best" stars, for an astronomer using an optical spectrograph, are the FGK stars: they tend to have a lot of relatively strong lines. Of course, the examples above show just a teeny-tiny section of the entire optical spectrum, so things might look slightly different toward the blue or red end of the spectrum; but remember that it's often necessary to average together results from thousands of lines in order to achieve the desired precision (around 1 m/s).
Consider these two spectra, both belonging to main sequence stars of spectral class F:
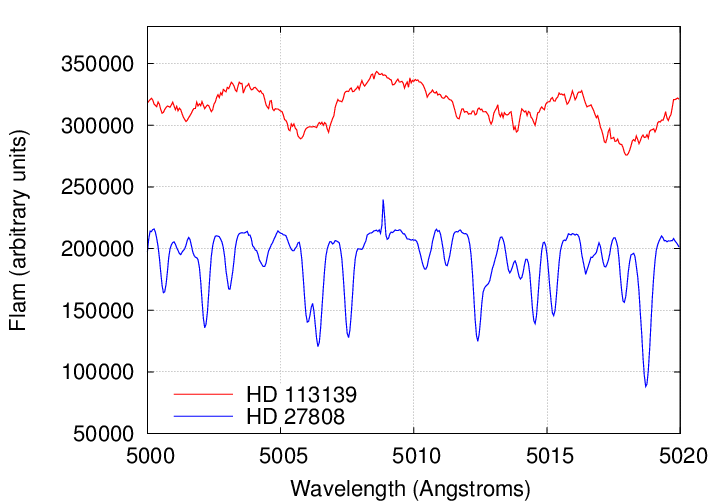
Data courtesy of the
Elodie archive
Q: Which star would yield better radial velocity
measurements? Why?
Clearly, HD 27808 would permit better measurements, due to its large number of sharper, deeper absorption lines. But if these are both type "F" stars, why the difference?
Q: Why is HD 27808 so much better than HD 113139?
Maybe this will help:
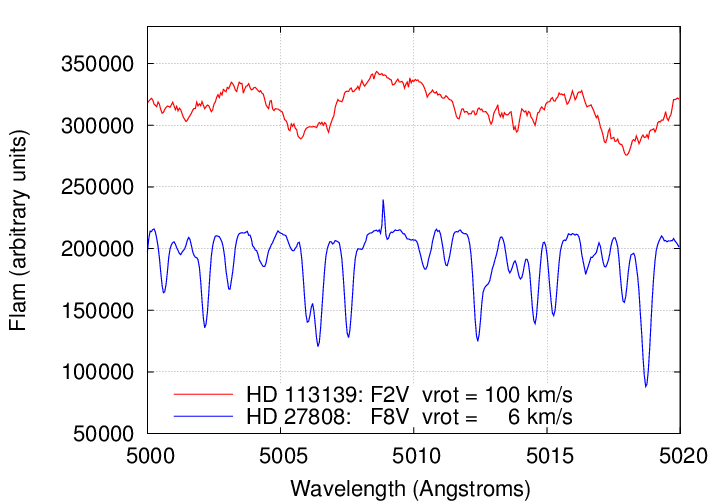
Data courtesy of the
Elodie archive
Turning raw spectra into clean spectra requires a lot of work with special reduction software. I can't talk about that here.
Calibrating spectra and measuring the positions of lines and calculating the radial velocity for a single spectrum is really complicated, too. You'll have to check out the technical literature for help with that.
But, once you have a series of radial velocity measurements, like this:
# JD velocity_(m/s)
2454602.85804 -187.65
2454603.10267 -198.11
2454603.86302 -142.90
it's not so hard. There are plenty of tools which have been written to analyze periodic signals (yeah, yeah, big surprise, right?). You can find a nice list of tools which are specially designed with astronomers in mind by looking at
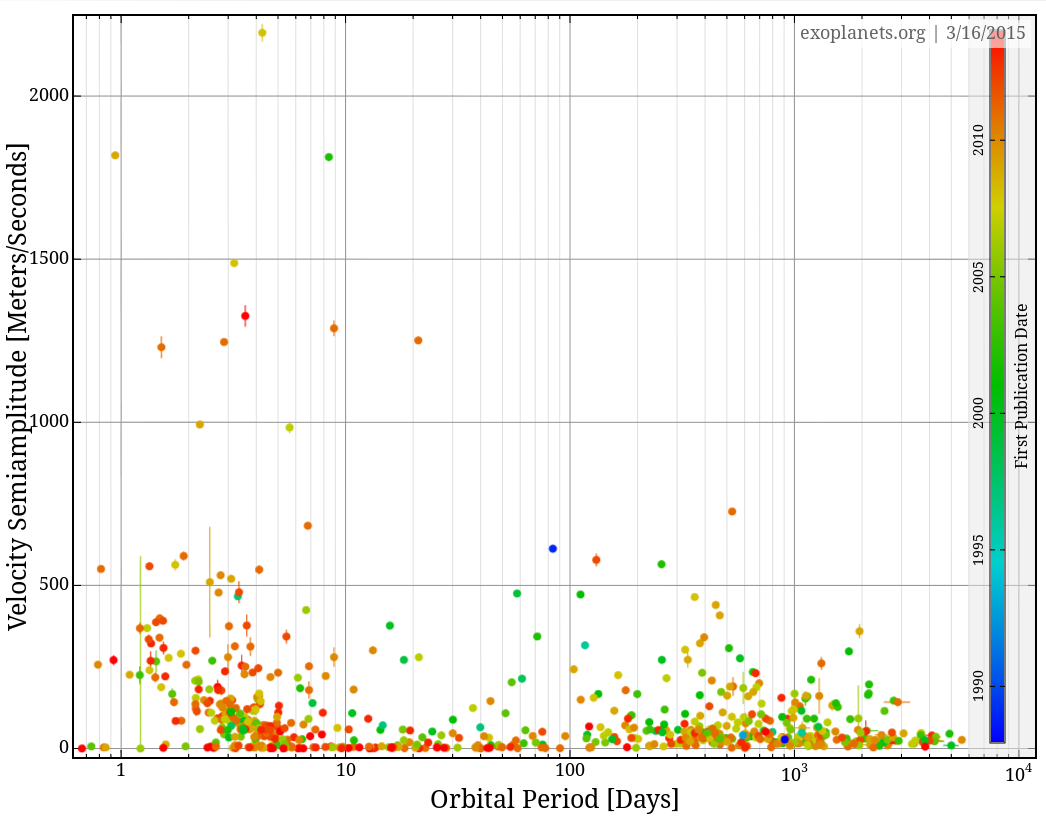
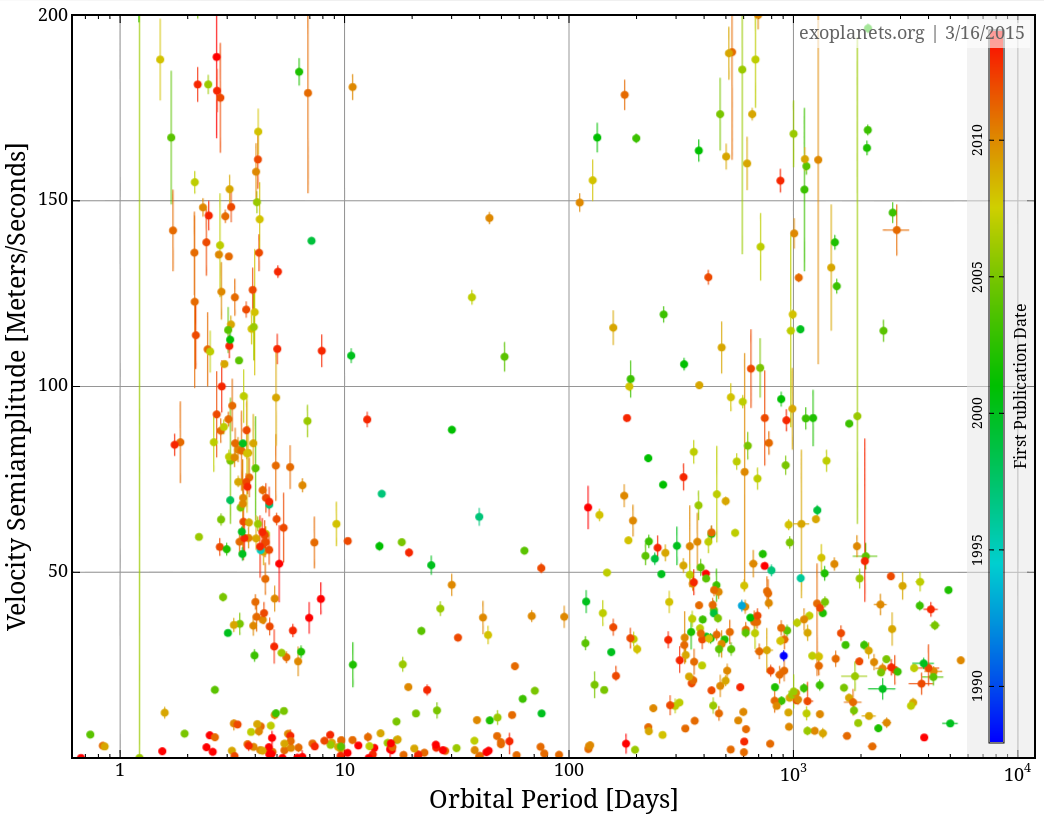
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.