Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
All spectroscopy involves the separation of light into its individual wavelengths (or energies, or frequencies). How can one do that?
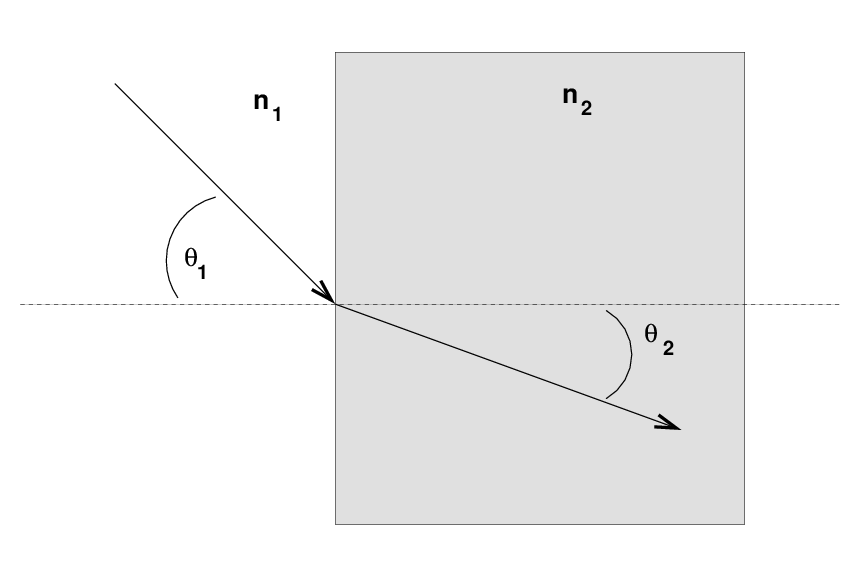
In the optical, there are two main methods. One relies upon refraction of light as it passes through a piece of glass or plastic. Remember what happens when light moves from air to glass (or vice versa)? Since the refractive index of glass is different than that of air, the light bends:
There's an equation which relates the angles of the light relative to the normal vector, before and after it enters the glass. Something about Snell ...
Q: What is the relationship between the angles θ1 and θ2?
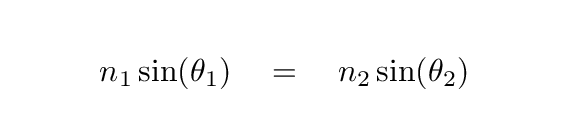
Now, this isn't enough on its own to help us form a spectrum. We need to pick a medium which not only refracts light, but refracts it by a degree which depends on the wavelength of the light. In other words, we need a dispersive medium in which the index of refraction depends on the wavelength, n = n(λ) .
In common materials, the index of refraction is larger for short wavelengths. That means
Q: Suppose you are interested in taking the spectrum of a really,
really faint galaxy, one for which every photon counts.
Do you see any drawback to using a prism of glass?
Right. Refractive optics require light to pass through some material, which can cause some photons to scatter or be absorbed, and so lost.
The other main method of forming a spectrum (can) avoid this problem, because one can use a REFLECTION off a polished surface, thus preserving more photons. This second method involves diffraction gratings.
For simplicity's sake, in the diagrams below, I'll show some gratings used in a transmissive, rather than reflective, manner. It just makes things easier to see. In most astronomical applications, though, light will bounce off a grating rather than going through it.
So, a diffraction grating is a device with many grooves or little openings through which light rays can pass. Let's shine light through these openings and onto a detector, over on the right-hand side of this diagram. Consider one location on the detector, marked with a "P" in the diagram.
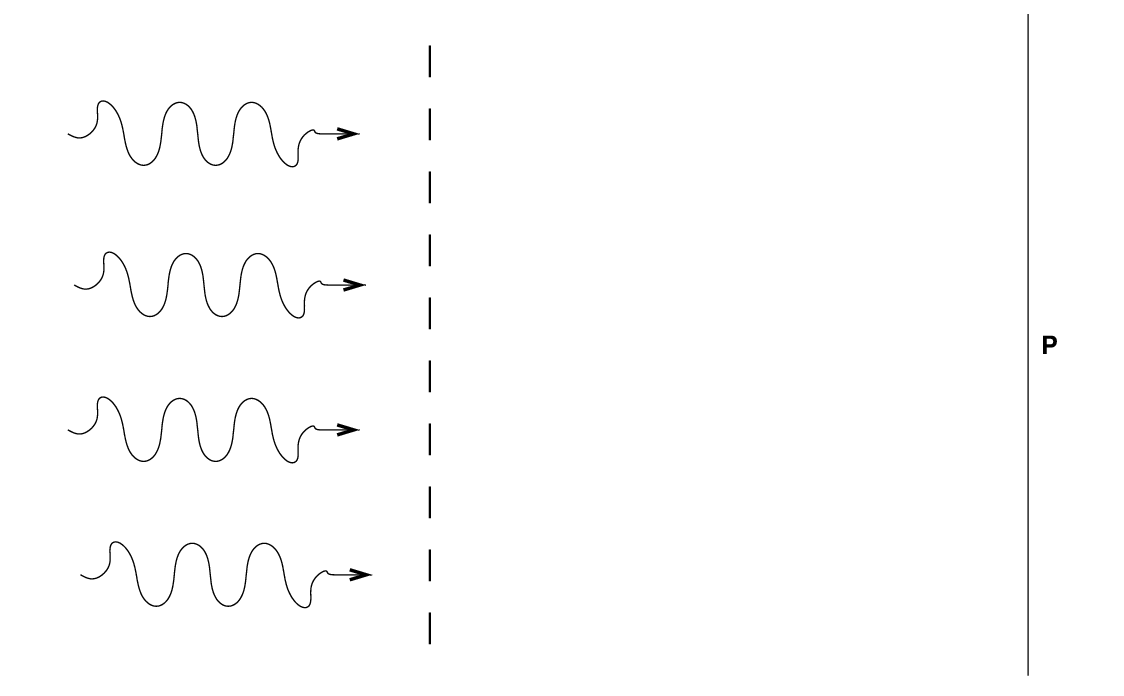
Now, a light ray coming from directly across from the "P" needs to travel a distance L to reach that spot on the detector. But light rays passing through an opening to one side -- a distance d or angle θ from the exact center of the grating -- must travel a slightly longer distance to reach the "P".
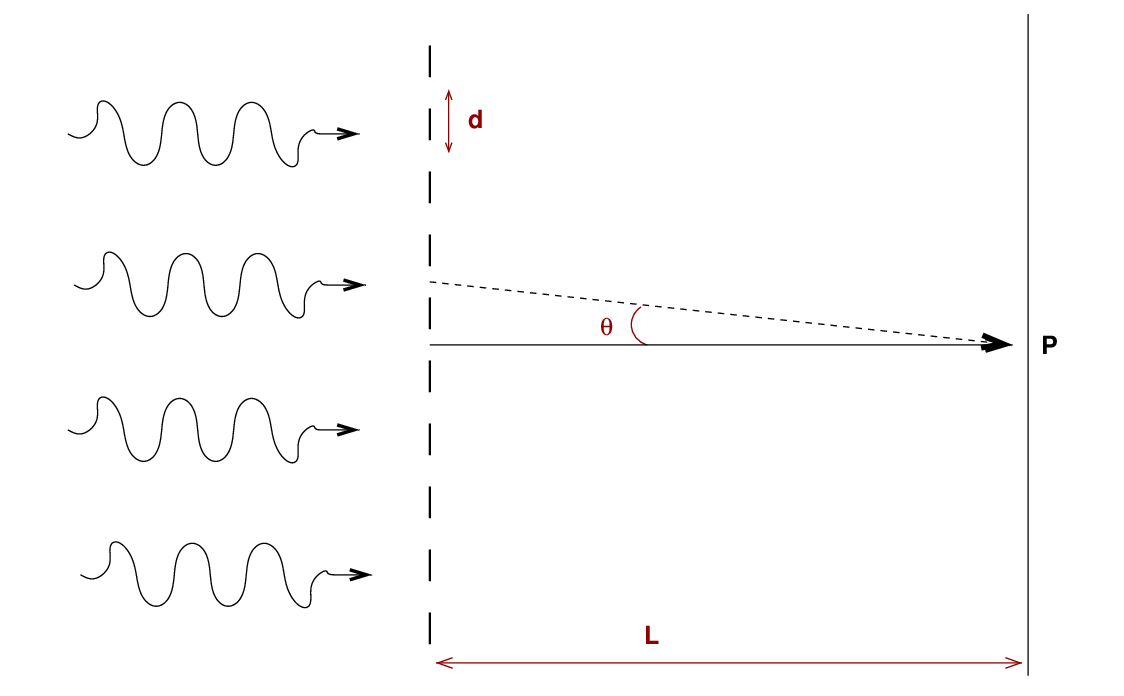
Q: How much extra distance must the second ray travel?
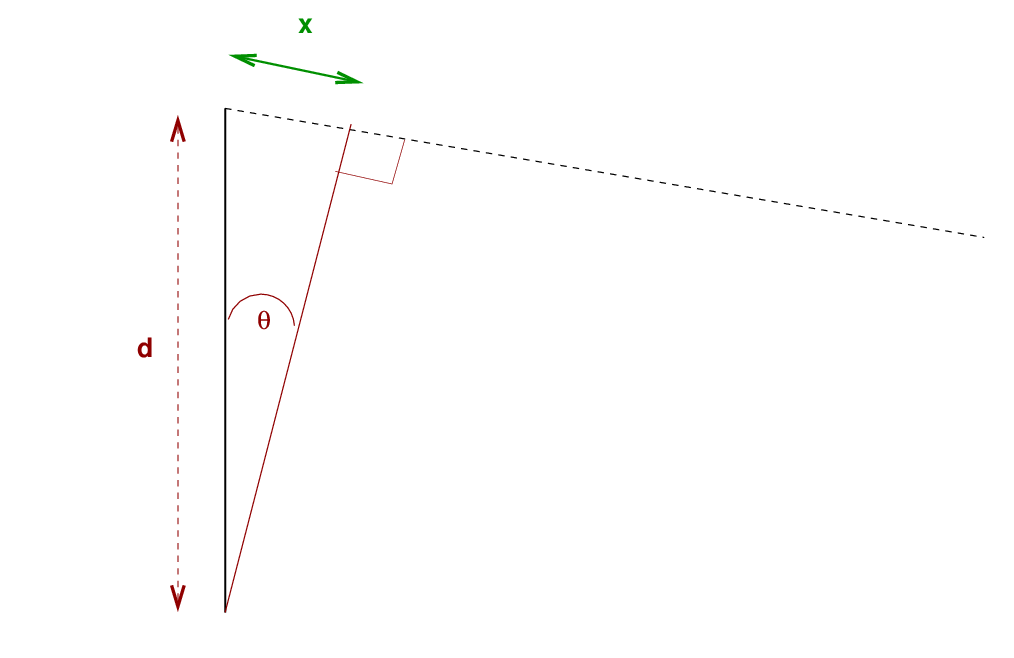
That extra distance is
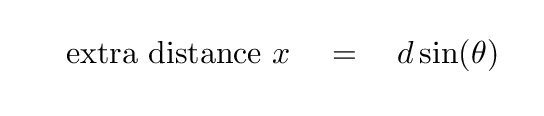
Now, if this extra distance is equal to an integral number of wavelengths of the light, then the second ray will interfere constructively with the central ray. That means that light striking the "P" on the detector will be particularly bright. In other words, we'll see a bright spot on the detector at position "P" if
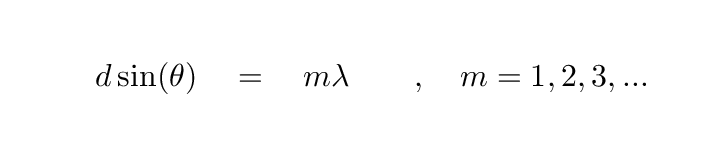
But the same is true if we look at things from a slightly different point of view. If we shine light of wavelength λ through a diffraction grating with spacing d between grooves, and the light travels a distance L before it reaches our detector, then we should see a bright spot at the very center of the detector -- straight across from the entrance, at "P"; but we should also see bright spots at off-center locations for which the angle θ satisfies this criterion.
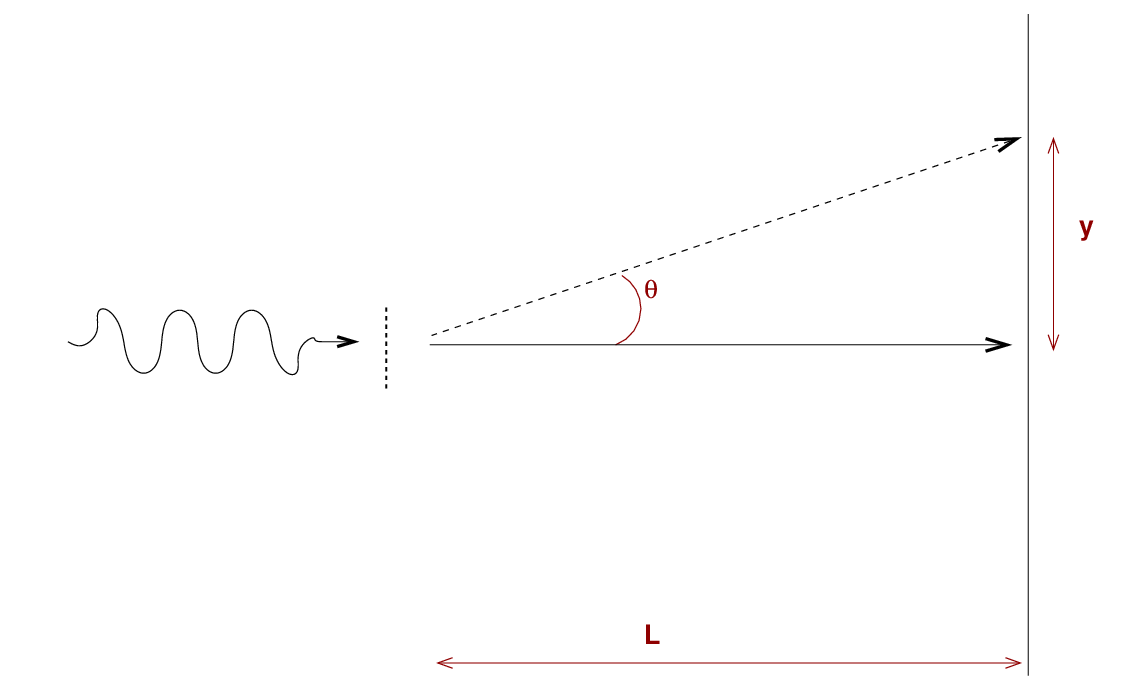
Note that diffraction gratings will
There are a number of ways that people have arranged optics and prisms and gratings to produce spectra. Some create the spectrum of a single object; others produce spectra for hundreds of objects at once.
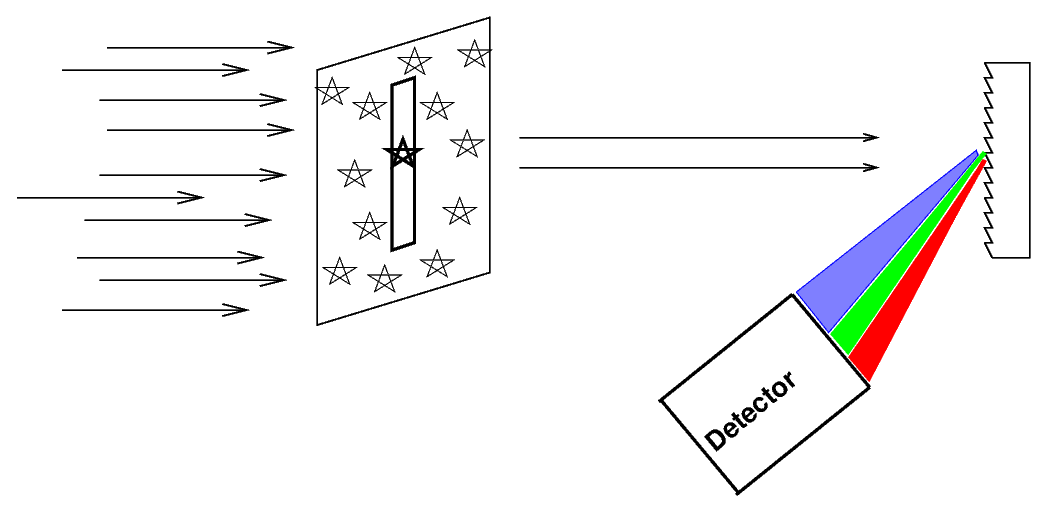
The spectrum produced in this way has a familiar form: a long, thin rectangle, due to the shape of the slit through which light passed. Absorption and emission lines appear as narrow vertical bars.
Image by Maurice Gavin, from
the wpo-amateur spectroscopy web site.
Image of objective prism of the Kiso Schmidt telescope courtesy
of Michael Richmond
Image courtesy of
M. Gavin
If you've ever heard of the Henry Draper (HD) catalog, or of the Harvard College Observatory computers, led by Annie Jump Cannon and Wilhemina Fleming, who created it, then you've used spectra created in this way.
This sort of "slitless spectroscopy" can create some cool images:
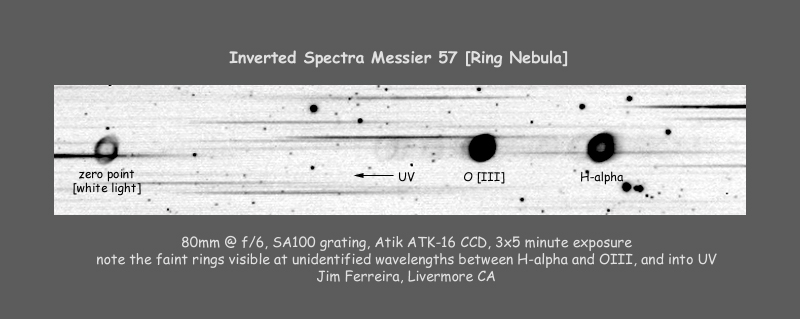
Image courtesy of
Jim Ferreira
The problem with some spectrographs is that they spread the light from a single object out into a very long, thin shape ... but that doesn't match the shape of our detectors. Most CCDs and other devices are roughly square, or slightly rectangular.
Is there any way to make a long, thin line fit onto a roughly square detector?
If we mount a spectrograph to the back of a big telescope, then as the telescope tracks and points, the spectrograph -- and all its optics and detectors -- will tilt from side to side. That can ruin the delicate optical alignment of some devices, degrading the quality of the measurements.
Q: Is there some way to separate the spectroscope
from the telescope?
Sure! Use an optical fiber to carry the light of one object from the telescope, to a spectrograph which sits motionless on the floor. Or in another room.
Here are pictures showing the fibers for the SDSS spectrograph being plugged into a metal plate, into which holes have been drilled at EXACTLY the positions of some stars and galaxies of interest.
Image courtesy of
the Sloan Digital Sky Survey
Image courtesy of
the Sloan Digital Sky Survey and BOSS
Now, a single fiber allows one to carry the light of a single object to the spectrograph -- but all the light of that object is mixed together. If we are studying a relatively nearby galaxy, that means that we mix up the light from the central nucleus and from the outer spiral arms or disk.
What if we could pack fibers very close together, so that one fiber measured the nucleus, but other fibers collected light from the disk or arms?
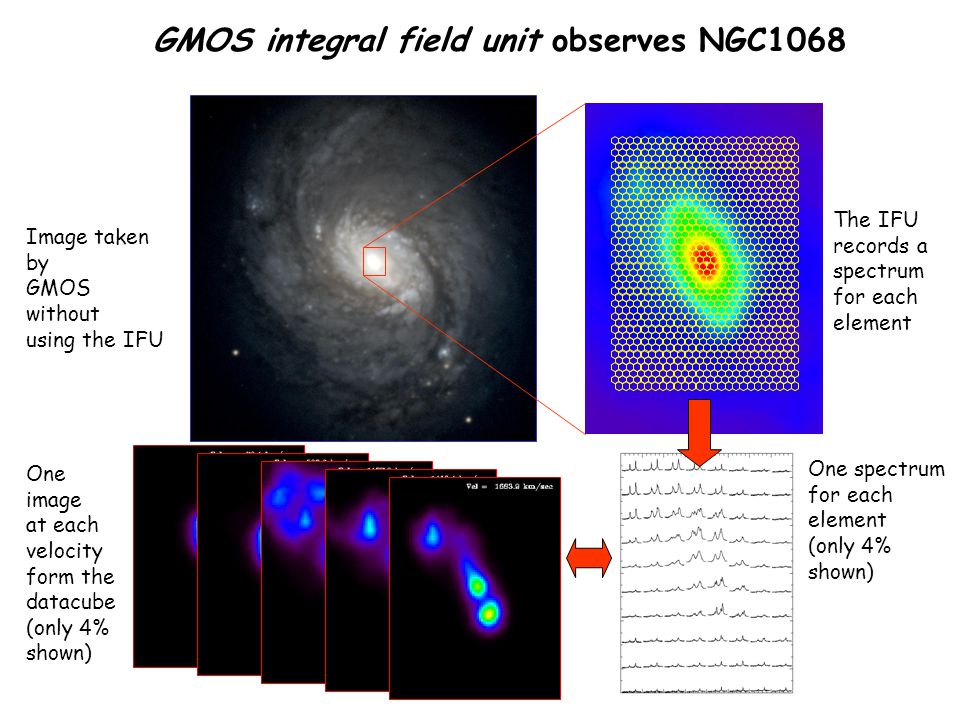
Image courtesy of
Jeremy Allington-Smith, University of Durham
Well, one doesn't have to use fibers -- there are several methods for sending light from closely packed regions in the focal plane to a spectrograph:
Image courtesy of
the Integral Field Spectroscopy Wiki
What are the advantages of spectroscopy over simple imaging? Well, in a simplified way, an image tells you "how bright is this star?" But what can you learn from spectroscopy?
Imaging Spectroscopy
--------------------------------------------------------
How bright is it?
So, if spectroscopy is so great, why don't ALL astronomers ALWAYS use spectrographs?
Q: Is there any advantage for a simple imaging camera
over a spectroscopic camera attached to the same telescope?
Well, yes. If you split up the light from an object into a spectrum, then you are spreading out the light from the object across your detector. That means that the number of photons which strike each little section of your detector is much smaller ... which means that the SIGNAL-TO-NOISE must decrease.
One of the most common measurements one can make of a spectrum is the equivalent width of a line.
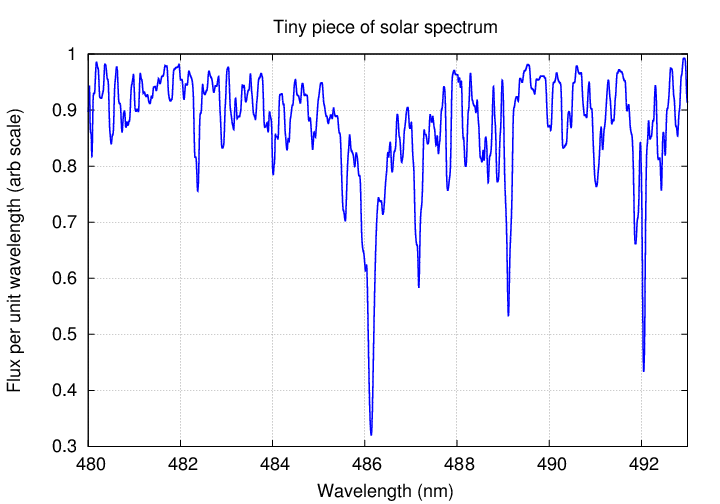
In the spectrum above,
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.