Joe the Astronomer has a telescope, CCD camera, and two filters: B and V. The manufacturer stated that they were made to the standard Johnson-Cousins filter specifications, as described in
Joe decides to make a little test of this claim. He chooses a field in which there is solid photometry: PG1633+009, one of the equatorial calibration fields listed in the paper

The paper by Landolt provides this photometry (which you can also find in the Vizier system at http://vizier.u-strasbg.fr/viz-bin/VizieR?-source=II%2F183A):
#Full RAJ2000 DEJ2000 Star RA2000 DE2000 Vmag B-V U-B V-R R-I
# "h:m:s" "d:m:s" "h:m:s" "d:m:s" mag mag mag mag mag
#
1 16 35 24 +09 47.8 PG1633+099 16 35 24 +09 47 50 14.397 -0.192 -0.974 -0.093 -0.116
2 16 35 26 +09 47.9 PG1633+099A 16 35 26 +09 47 53 15.256 0.873 0.320 0.505 0.511
3 16 35 34 +09 46.4 PG1633+099B 16 35 34 +09 46 22 12.969 1.081 1.007 0.590 0.502
4 16 35 38 +09 46.3 PG1633+099C 16 35 38 +09 46 16 13.229 1.134 1.138 0.618 0.523
5 16 35 40 +09 46.7 PG1633+099D 16 35 40 +09 46 43 13.691 0.535 -0.025 0.324 0.327
Notice that the stars cover a wide range of colors, with -0.192 < (B-V) < 1.134. The key to measuring color terms is to have simultaneous measurements of stars over as wide a range of colors as possible.
Joe takes a set of images of this field with his camera using both the B and V filters. He measures the brightness of the stars on each exposure and converts the raw counts to an instrumental magnitude. His data looks like this:
# star b v
PG1633 16.759 15.749
PG1633A 18.812 16.602
PG1633B 16.878 14.348
PG1633C 17.242 14.582
PG1633D 16.905 15.050
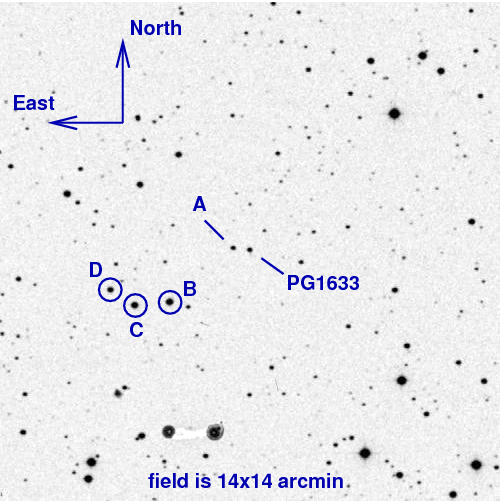
"In order to calibrate my photometry," thinks Joe, "all I have to do is to shift my measurements by a constant value, so that the instrumental magnitudes match up with the catalog magnitudes from Landolt's paper." However, because Joe fears his filters might have some problem, he decides to test this idea by plotting the results as a function of the instrumental colors of the stars. In other words, Joe

"Excellent!" exclaims Joe. "The difference between my measurements and the catalog values is the same for all the stars, both red ones and blue ones. I can simply average the differences to find the simple shift which will convert my instrumental "v" magnitudes into the standard Johnson "V" magnitudes."
Joe finds that the required shift is 1.36 magnitudes, so that
Landolt V = instrumental v - 1.36 (+/- 0.01)
On the other hand, when Joe compares the instrumental b-band magnitudes to the catalog magnitudes, he finds a different situation:

"Uh-oh!" says Joe. "The difference here depends on the color of the star: blue stars have smaller differences than red ones. If I try to use a constant shift to convert the instrumental magnitudes to catalog magnitudes, I'll end up with systematic errors ... and pretty big ones, too."
Joe decides that he can fit this data with a linear relationship, like this:
Landolt V = instrumental v + z + k*(b - v)
where z is a zero-point shift, k is the first-order color term, and (b - v) is the instrumental color of the star. His calculator can do the arithmetic, finding the best-fit values of
z = 2.34 +/- 0.08
k = 0.19 +/- 0.04
"Well," says Joe, "I guess that my B filter isn't quite the same as the standard B filter. Still, as long as I include this extra term in my analysis, I can report my magnitudes on the standard Johnson magnitude scale."
There are many fields throughout the sky with good photometry and stars covering a broad range of colors. The Landolt paper mentioned above is a good source of such fields; I'll pick out 4 of my favorites. I'll also include the cluster M67, which has been used by a number of authors for photometric calibration:
Field center (J2000) 02:33:41 +05:18:40
#Full RAJ2000 DEJ2000 Star RA2000 DE2000 Vmag B-V U-B V-R R-I
"h:m:s" "d:m:s" "h:m:s" "d:m:s" mag mag mag mag mag
1 02 33 28 +05 19.7 PG0231+051E 02 33 28 +05 19 44 13.804 0.677 0.201 0.390 0.369
2 02 33 33 +05 19.5 PG0231+051D 02 33 33 +05 19 28 14.027 1.088 1.046 0.675 0.586
3 02 33 40 +05 17.6 PG0231+051A 02 33 40 +05 17 38 12.772 0.710 0.270 0.405 0.394
4 02 33 41 +05 20.3 PG0231+051C 02 33 41 +05 20 19 13.702 0.671 0.114 0.399 0.385
5 02 33 41 +05 18.7 PG0231+051 02 33 41 +05 18 40 16.105 -0.329 -1.192 -0.162 -0.371
6 02 33 45 +05 17.5 PG0231+051B 02 33 45 +05 17 30 14.735 1.448 1.342 0.954 0.998

Field center (J2000) 09:21:28 +02:46:03
#Full RAJ2000 DEJ2000 Star RA2000 DE2000 Vmag B-V U-B V-R R-I
"h:m:s" "d:m:s" "h:m:s" "d:m:s" mag mag mag mag mag
1 09 21 22 +02 47.5 PG0918+029D 09 21 22 +02 47 30 12.272 1.044 0.821 0.575 0.535
2 09 21 28 +02 46.1 PG0918+029 09 21 28 +02 46 03 13.327 -0.271 -1.081 -0.129 -0.159
3 09 21 34 +02 48.0 PG0918+029B 09 21 34 +02 48 01 13.963 0.765 0.366 0.417 0.370
4 09 21 35 +02 46.3 PG0918+029A 09 21 35 +02 46 20 14.490 0.536 -0.032 0.325 0.336
5 09 21 42 +02 46.6 PG0918+029C 09 21 42 +02 46 38 13.537 0.631 0.087 0.367 0.357
Field center (J2000) 16:35:24 +09:47:50
#Full RAJ2000 DEJ2000 Star RA2000 DE2000 Vmag B-V U-B V-R R-I
# "h:m:s" "d:m:s" "h:m:s" "d:m:s" mag mag mag mag mag
#
1 16 35 24 +09 47.8 PG1633+099 16 35 24 +09 47 50 14.397 -0.192 -0.974 -0.093 -0.116
2 16 35 26 +09 47.9 PG1633+099A 16 35 26 +09 47 53 15.256 0.873 0.320 0.505 0.511
3 16 35 34 +09 46.4 PG1633+099B 16 35 34 +09 46 22 12.969 1.081 1.007 0.590 0.502
4 16 35 38 +09 46.3 PG1633+099C 16 35 38 +09 46 16 13.229 1.134 1.138 0.618 0.523
5 16 35 40 +09 46.7 PG1633+099D 16 35 40 +09 46 43 13.691 0.535 -0.025 0.324 0.327

Field center (J2000) 22:16:28 -00:21:15
#Full RAJ2000 DEJ2000 Star RA2000 DE2000 Vmag B-V U-B V-R R-I
"h:m:s" "d:m:s" "h:m:s" "d:m:s" mag mag mag mag mag
1 22 16 18 -00 22.2 PG2213-006C 22 16 18 -00 22 15 15.109 0.721 0.177 0.426 0.404
2 22 16 22 -00 21.8 PG2213-006B 22 16 22 -00 21 49 12.706 0.749 0.297 0.427 0.402
3 22 16 24 -00 21.4 PG2213-006A 22 16 24 -00 21 27 14.178 0.673 0.100 0.406 0.403
4 22 16 28 -00 21.2 PG2213-006 22 16 28 -00 21 15 14.124 -0.217 -1.125 -0.092 -0.110
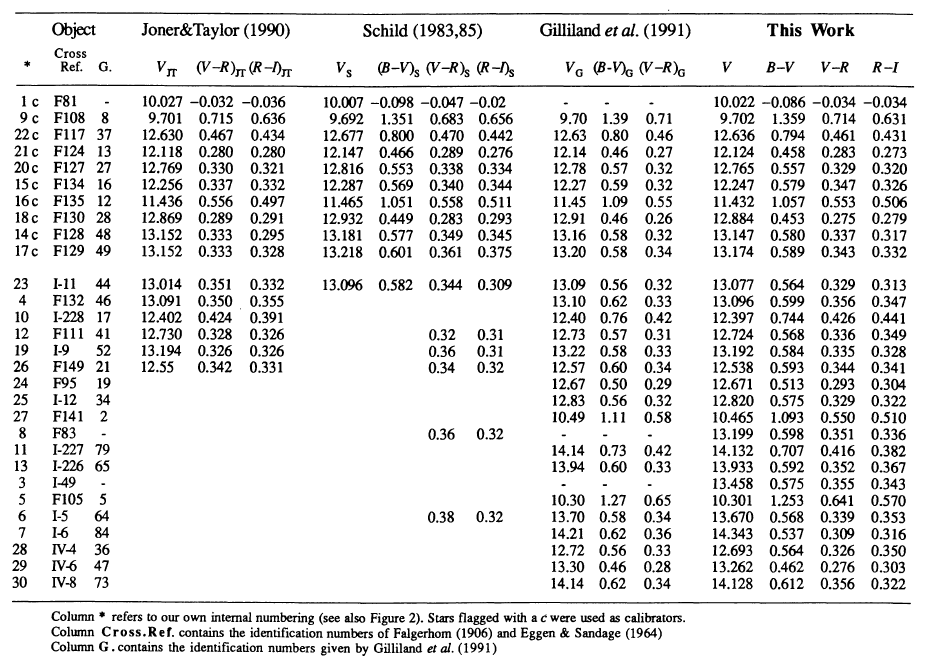
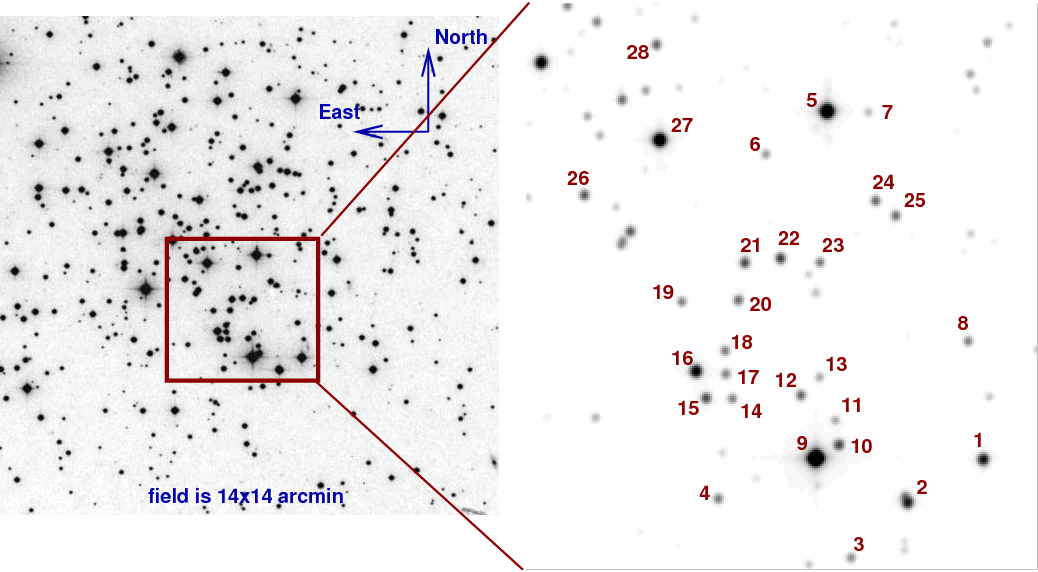
Field center (J2000) 08:51:21 +11:46:16. The table below is from Chevalier and Ilovaisky, A&AS 90, 225 (1991)
Last modified 9/05/2011 by MWR.