Nick Mostek and I used the WIYN 0.9m telescope with the MOSAIC camera in late May, 2002, to observe an area close to the SNAP Northern Field. Actually, at the time, we thought it was the SNAP field, but it has since been moved; I therefore refer to it as the "OSNF" throughout this document.
We had one very good night: May 28, 2002. Although there was bright moonlight, the sky was clear and almost cloudless from dusk to dawn. We observed the OSNF itself ("center") as well as a field about half a degree to the east ("east"). We acquired images of selected fields with Landolt standards throughout the night as well.
Recall that the MOSAIC camera consists of eight chips, each 2048x8192, arranged to make a square roughly one degree on a side. The plate scale is 0.43 arcsec per pixel. Our strategy was to take 2 or 3 images in each passband at each pointing (center or east) and each exposure time (1, 10, or 100 seconds).
Nick took the images back to U of Indiana, where he performed all the basic processing to "clean" the images: bias subtraction, flatfielding, and some quality control. I then copied the images to RIT and measured the properties of stars in the frames.
One of the main results is this table of stars: it provides astrometry and photometry for objects which appeared in all four of our passbands (V, I, M and D51). The astrometry is based on our own images, using the USNO-A2.0 as a reference catalog and reducing each chip individually. The photometric calibrations assume that all eight chips in MOSAIC share the same color terms and zero points, which is manifestly not true (as we will show, below).
This list contains 1574 stars, which were detected in all four passbands. I reduced the data in two passes: one for V and I, the other for M and D51. Stars without matching detections in each pair of bands were discarded (thus, many faint stars clearly detected in M-band do not appear, because they did not also appear in D51 images).
The V and I magnitudes are based on an all-sky solution for the entire night using the Landolt standards, with color terms in (V-I) and extinction.
true_mag = raw_mag + a + b*(raw_color) - k*(airmass)
N a b k RMS
-----------------------------------------------------------------------------
V 273 -3.133 0.027 -0.030 0.017 0.183 0.019 0.020
I 273 -3.637 0.023 -0.021 0.015 0.093 0.017 0.019
The M and D51 magnitudes are determined in the following manner:
M = (instr. m) + offset_m
D51 = (instr. d51) + offset_d51
in other words, no color terms, no extinction. The fixed
offset for each passband was calculated to cause stars
with (V-I) colors between 0.5 and 0.8 to have
similar V and M (or D51) magnitudes.
Here are the first few lines in the big star list:
0 248.85420 56.06415 16.935 0.003 16.467 0.002 16.952 0.026 16.684 0.130
1 248.85623 56.11577 16.827 0.007 15.959 0.012 16.828 0.044 16.698 0.095
3 248.85717 55.54873 15.216 0.006 14.530 0.006 15.141 0.003 15.061 0.020
The mean and stdev are calculated from weighted collections of measurements on frames of different exposure length. To avoid saturation and excessive scatter near the plate limit, I chose to collect stars like so:
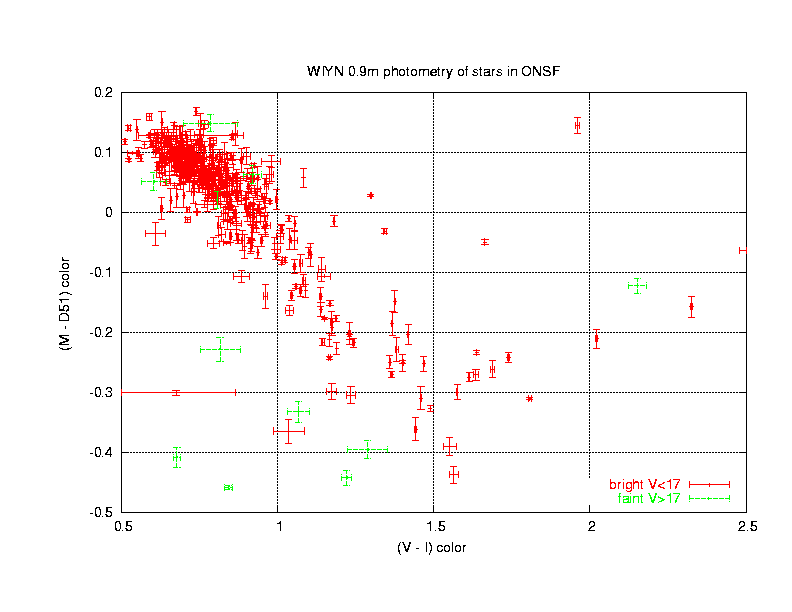
One of our main goals was to identify stars which might be cool giants, since they may be good stars to use in transferring photometric calibration. As explained in this document, one can use the difference in magnitude in broad-band and narrow-band filters to distinguish giants from dwarfs. Below is a graph in which we plot this magnitude difference (M - D51) versus temperature (as indicated by (V-I) color). Click on the graph to download a Postscript version.
There is clearly a locus of points from the clump at upper left down towards the middle bottom of the graph; these are dwarfs. There are a very few stars with (V-I) colors between +1 and +2 which fall above this locus: these are possibly giant stars.
This graph shows only stars with excellent photometry in all passbands: stdev < 0.02 mag. I have identified candidates with mediocre and poor photometry as well. In the lists you may download below, the best candidates appear first, then a blank line, then the candidates with mediocre photometry, another blank line, and finally the candidate with poor photometry.
A second hint to a star's luminosity class may come from its proper motion: for a given apparent magnitude, dwarfs are likely to be nearby, and so move across the sky relatively quickly, while giants must be far away and, thus, probably move slowly. I started to compare my positions (epoch 2002) to those from the USNO-A2.0 catalog (epoch 1955ish) to determine the proper motion of the giant and dwarf candidates. However, I discovered that the USNO-B1.0 catalog contains proper motions for all stars in our images. I checked several of the values based on our images to those in the USNO-B1.0, and found that they were consistent. One can therefore simply look up the proper motions from the USNO-B1.0 for any desired candidates.
This table may help to interpret the proper motions:
apparent magnitude mV
13 14 15 16 17
------------------------------------------------------------------------
If a giant,
at dist (pc) 2500 4000 6300 10000 16000
v = 50 km/s
prop motion ** 0.2 0.1 ... ... ...
v = 300 km/s
prop motion ** 1.2 0.8 0.5 ... ...
If a dwarf
at dist (pc) 100 160 250 400 630
v = 50 km/s
prop motion ** 5.1 3.2 2.0 1.3 0.8
v = 300 km/s
prop motion ** 30 19 12 7.7 4.9
---------------------------------------------------------------------------
The proper motions listed in the table are arcseconds of motion expected over a fifty-year baseline; that is, the proper motions between the 1950ish POSS I and USNO-A2.0, and the WIYN measurements in 2002. Our astrometry was good to around 0.8 arcsec, so, in short, if we could detect any proper motion, the star was probably a dwarf.
Of the 8 best candidate giant stars,
Since the MOSAIC camera is made of eight different CCD chips, one might guess that reduction of its photometry might be difficult. To do a proper job, one ought to treat each of the 8 chips independently. But that means dithering stars across each of the 8 chips, which means lots and LOTS of exposures, and a huge amount of reduction.
We took the easy way out: treat the entire camera as a single detector. This isn't a completely crazy idea, as this excerpt from a Kitt Peak document on MOSAIC photometry indicates:
* Do aperture photometry on the stacked images. Variations in the aperture corrections and color-terms probably will limit this photometry to 2%.* If aperture photometry is just not good enough (too much crowding), you will achieve a significant improvement by doing 40x more work and treat each CCD of each dithering separately than trying to do PSF fitting on the stacked images.
Our measurements of the Landolt standards showed a scatter of about 2 percent, in line with this very rough estimate. Fine.
But is there really a difference between measurements made on different chips? Recall that we observed two fields, "center" and "east". A strip of sky roughly 60 by 10 arcminutes appeared in both fields. Consider only our 100-second V and I exposures. We acquired 4 measurements of each star in each passband: two on one chip (in the "center" field), and two on a different chip (in the "east" field). We can define 6 differences with these 4 magnitudes:
If the entire array behaves like a single monolithic detector, then these differences should form a uniform set. But if the individual chips have significantly different properties, we would expect the "same chip" differences to be smaller than the "difference chip" differences. Below is a graph showing the standard deviation of these differences as a function of magnitude. Look at the red and green points. First, V-band:
Now I-band:
The blue dots show the scatter due to photon noise alone, which dominates at faint magnitudes. Note that the measurements on a single chip do show less scatter than those on different chips, at least until the photon noise takes over.
In short, we agree with Phil Massey (author of the study at Kitt Peak) that the MOSAIC chips are not identical. Is that important? The chip-to-chip variations of a percent or two increase the uncertainty in photometric measurements of stars. Note that the difference between giants and dwarfs in the diagnostic color-color diagram above is about 0.20 mag. For distinguishing giants from dwarfs, an extra percent or two isn't critical; but for measuring the magnitudes of local standards in the SNAP calibration procedures, it would be very bad.