
Table of Contents
Send a free-flying spacecraft into low earth orbit (LEO).
Place on board:
Because this spacecraft will look only at relatively bright stars, it is free of many of the complicating factors which make conventional space telescopes so expensive and complex. Examples:
This doesn't need to be the Hubble Space Telescope. A better comparison is the MOST satellite:

The main advantage of a freeflyer over a rocket-bourne instrument is that one has an additional reference source: the Sun.
If one does not believe that the Sun provides a good secondary reference, then the freeflying satellite provides no signficant advantage over a rocket-borne instrument for SNAP calibration.
There are several instruments which currently (or in the near future) measure the solar irradiance. For example,
By using the Sun as a reference source, we let other groups do much of the hard work.
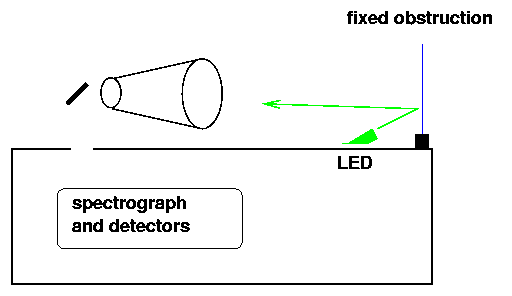
We can, of course, include several on-board sources as additional references, just to verify that the instruments are not suffering significant contamination or degradation. LEDs are a reasonable choice, and the "fixed obstruction" method mentioned below provides a natural way to send light from an LED through the main optics into the detector.
How can we measure sunlight through the very same optical path as starlight? Two options involve reflected sunlight.


Method Pro Con
---------------------------------------------------------------------
shoot "nerf balls" no effect on ordinary only a few chances
observations moving parts
objects in focus requires tracking balls
cannot check reflectance
fixed obstruction will definitely be object not in focus
recorded small effect on ordinary
observations
can check reflectance
---------------------------------------------------------------------
Each method has its advantages and disadvantages.
The analysis of the "nerf ball" method is relatively simple: each ball (eventually) becomes a point source in images and can be compared easily to stars. The analysis of the "obstruction" method is more difficult: since the object will be very far from focus, its light will appear as a diffuse background on images. Nevertheless, as the satellite passes into and out of the Earth's shadow, one can measure the change in this background accurately; it is a matter of geometry and optics to convert the background into an effective solar irradiance.
On the other hand, the logistics of making the measurements favors the fixed obstruction. The MSX experiment fired five spheres away from the satellite, but managed to track only two of those completely as they moved away from the spacecraft. The obstruction is always in the same place, and never has to move. Moreover, one can shine an internal light source onto the obstruction while in the Earth's shadow to check the reflectivity of the obstruction, both as a function of wavelength, and as a function of time on orbit.
How large must the telescope be? Suppose we wish to observe zeroth-magnitude stars like Vega. Vega produces roughly 500,000 photons per second per square centimeter of collecting area through a wide-band filter in the visible. Thus, a telescope with a diameter of D = 10 cm will collect through a wide-band filter roughly
2
N = 500,000 photon/sec * pi * (5 cm)
= 40,000,000 photon/sec
A V-band filter has resolving power R = 6 or so. If we send the light into a spectrograph with resolving power R = 1000, we divide this number of photons by roughly 1000/6 = 166, leaving about 240,000 photons per second into each spectral bin.
Spreading this light over 10 or so pixels of a spectrograph camera per spectral bin reduces the number of photons per second per pixel to roughly 24,000. Assuming an overall efficiency of 1 percent in the telescope optics plus spectrograph optics plus detectors, we arrive at roughly
2
( D )
240 * ( ------ ) (photons/sec) per pixel from Vega
( 10 cm )
Even this small telescope can collect hundreds or thousands of photons per pixel in a few seconds from a star of magnitude zero.
Now, a small telescope will provide wide field of view. Each pixel in the detector will cover a relatively large area on the sky, perhaps 10 or 100 square arcseconds. However, the very bright stars we observe will still overwhelm the background. These large pixels make tracking simple: keeping the craft pointed to within a few arcseconds is probably good enough.
If one builds an instrument which permits long exposure times, then one can calibrate fainter stars. Using the canonical D = 10 cm telescope, a fifth magnitude star would produce several photons per second per pixel. The current SNAP detectors have dark current of roughly 0.0005 electrons per second per pixel in the visible, 0.04 electrons per second per pixel in the near-IR, so even a fifth magnitude star would provide over ten times as many photoelectrons as thermal electrons. With an exposure of 10 minutes = 600 seconds, one would collect 2000 photons per pixel.
Tenth magnitude stars would be much too faint to observe with a D = 10 cm telescope, as dark current would overwhelm the signal.
Scientific criteria only:
Other criteria: