How can we check for systematic errors in SNAP photometry? I suggest that the spacecraft follow a series of motions which will shift stars across individual chips, onto neighboring chips, and around the entire focal plane. By taking a series of exposures of the same star field at all these positions, and comparing the relative magnitudes of stars at various positions, we can detect and correct for a number of effects.
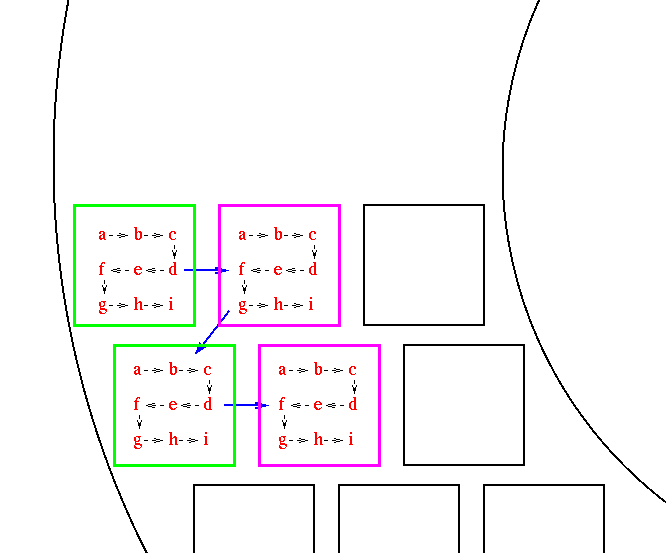
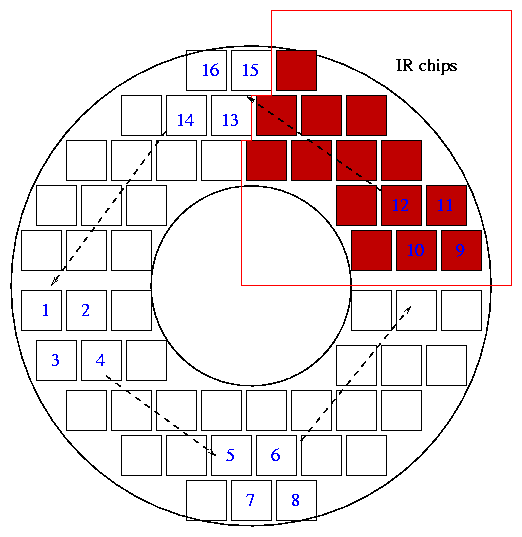
We can break up the spacecraft motions into "small" and "large" categories. Small shifts move a star from one location on a chip to another on the same chip, or from one chip onto a neighboring chip. A schematic of the SNAP focal plane shows one possibility:

A star is placed at each point of a 3-by-3 grid within each chip, then moved to an adjacent chip, moved over another 3-by-3 grid, and so forth. As indicated by the colored borders, neighboring chips should have different filters; however, it is very important that at least two chips of each filter are included in the serpentine track followed by a star.
Large shifts move a star from one quadrant of the focal plane to another. If the camera has IR detectors gathered in a single quadrant, large shifts are necessary to switch a star from visible to IR measurements.
As ground-based astronomers have discovered, even the best flatfielding schemes can leave systematic errors of several percent (!) in the apparent magnitude of a star as it moves from one place in the focal plane to another. One way to detect (and remove) position-dependent errors is to make a set of observations, moving the field of view slightly after each exposure, and then solve a big least-squares matrix. See, for example, a paper by Manfroid, Stellar calibration of CCD flat fielding , A&A Suppl, 113, 587 (1995).
For example, something like the following scheme might be necessary.
given instrumental magnitude m(i, j, k, x, y)
where
i is index of star in some master list
j is index of this exposure
k is index of CCD in array
x is row position of star on this CCD
y is col position of star on this CCD
we find the corrected magnitude M(i) via
M(i) = m(i, j, k, x, y) + a + b * x + c * y
k k k
+ d * x*x + e * x*y + f * y*y
k k k
where
a is a zero-point term, one per chip
b,c remove linear trends across each chip
d,e,f remove quadratic trends across each chip
This particular scheme yields 6 coefficients per chip. In order to find these unknown coefficients, one sets up a large system of linear equations like so:
m + a + b *x + c *y + d *x*x + e *x*y + f *y*y = M
11 k k k k k k 1
m + a + b *x + c *y + d *x*x + e *x*y + f *y*y = M
12 k k k k k k 1
m + a + b *x + c *y + d *x*x + e *x*y + f *y*y = M
13 k k k k k k 1
m + a + b *x + c *y + d *x*x + e *x*y + f *y*y = M
21 k k k k k k 2
...
m + a + b *x + c *y + d *x*x + e *x*y + f *y*y = M
ij k k k k k k i
The set of equations can be solved by standard least squares techniques.
At a guess, the very simple scheme shown above might involve
Remember, these corrections are determined and applied AFTER the images have been processed in the usual fashion (dark subtraction, overscan subtraction, flatfielding) and turned into lists of stellar magnitudes and positions. They are designed to remove low-frequency effects: not pixel-to-pixel variations, but gradual changes in effective sensitivity spanning significant fractions of a chip. The high-frequency effects must be dealt with by ordinary flatfielding.
The systematic differences discovered by this process will uncover (at least) the following:
If neighboring chips have different filters, then we automatically measure colors for (most of? all of?) the stars in the field.