There has been much recent discussion of the consequences of errors in the absolute flux calibration of the SNAP photometry. This note shows how different methods of analysis can change those consequences.
I make simplifying assumptions:
If the SNAP telescope is the only device used to observe the supernovae used in cosmological analysis, then there is no need to compare SNAP photometry to that from any other telescope. In that case, there can be no errors introduced by zero-point differences in the magnitude scale between SNAP and another observatory. There is also no need to put SNAP photometry onto a standard magnitude scale, such as the Johnson-Cousins or Mauna Kea IR system.
I assume from this point on that SNAP measurements of SNe Ia are the only supernova measurements used for cosmological analysis.
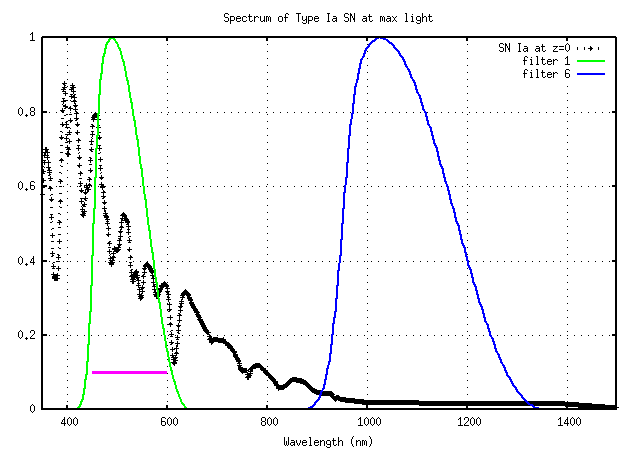
One approach to deriving the relative brightness (and hence distance) to two supernovae is to look at the same part of the rest-frame spectrum in each. At redshift z=0, for example, the rest-frame spectrum between 450 and 600 nm falls within SNAP filter 1:

At redshift z=1, on the other hand, this same portion of the rest-frame spectrum falls within SNAP filter 6:
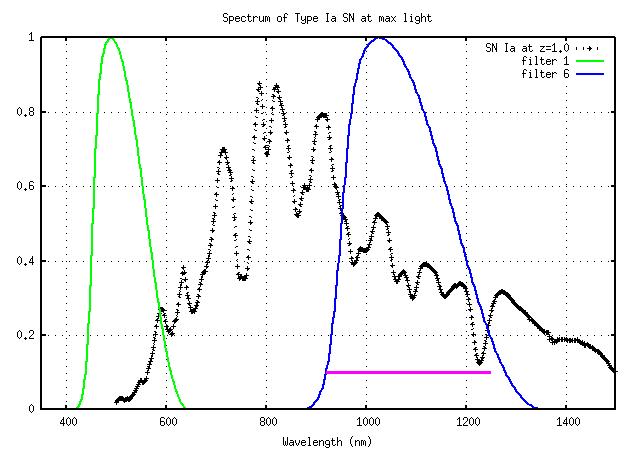
If we focus on this portion of the rest-frame spectrum, perhaps because we know the most about it in local supernovae, or perhaps because we believe that it should be the most identical in different events, then we use the following difference in magnitude as a starting point in the analysis:
delta_mag = (mag in filter 1 at z=0) - (mag in filter 6 at z=1)
Note that any error in the zero-point of filter 1 will combine with an error in the zero-point of filter 6 to create an overall error in this difference delta_mag.
Errors in the edges or shape of the filter passbands will likewise cause independent errors in instrumental magnitudes of each filter, which will again combine to create a larger overall error in the delta_mag value.
This approach of comparing the instrumental magnitude of a nearby supernova in filter X with that of a distant supernova in filter Y (which is redward of X) is I believe the one which SNAP is focusing on at the present time. The term "K-corrections" will appear in this sort of analysis.
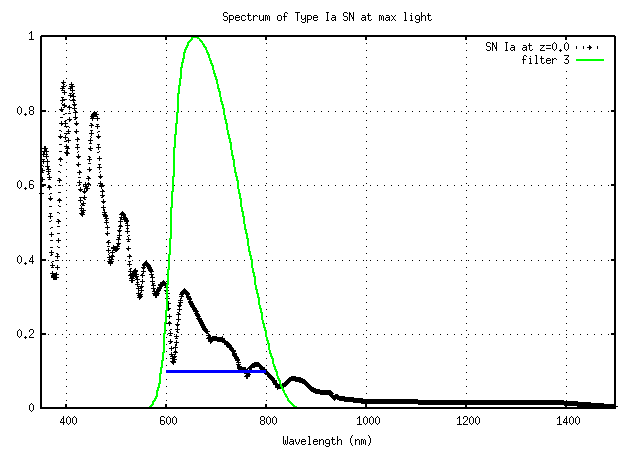
If we know the spectrum of a SN well over a wide range of wavelengths, then another option is available to us. We can look only at a single bandpass, which will sample different portions of the spectrum at different redshifts. For example, if we know the spectrum over the range 400 - 1000 nm, then the SNAP filter number 3 will sample a portion of this known range at redshift z=0: the rest-frame spectrum from 600 - 800 nm
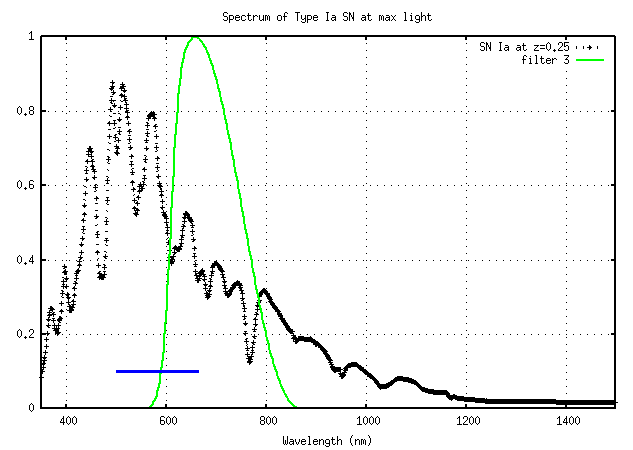
At redshift z=0.25, the filter number 3 will sample another portion of the rest-frame spectrum, from about 500 - 670 nm
At redshift z=0.5, this filter will sample the rest-frame spectrum from about 400 - 530 nm
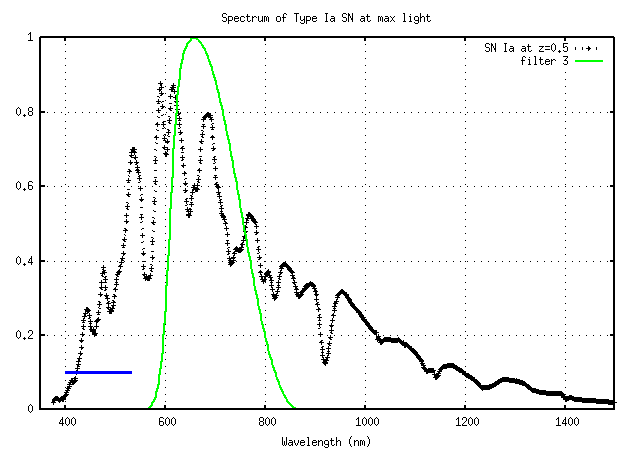
We can define the magnitude differences between supernovae at different redshifts observed through this filter alone:
delta_mag = (mag in filter 3 at z=0) - (mag in filter 3 at z=0.5)
In this way, an zero-point error in the calibration of passband 3 is cancelled. We do not need to know the absolute calibration of bandpass 3 at all. Nor do we need to know even the relative calibration of bandpass 3 to bandpass 5, or bandpass 6.
However, do note that any errors in the shape or position of each bandpass will cause systematic errors between our instrumental magnitudes and those calculated from the known spectrum of a SN Ia; that would cause systematic errors in the analysis.
In order for this approach to work, we need to have a wide range over which the "perfect" Type Ia spectrum is known. The wider this range,
For example, if we know the rest-frame spectrum over the narrow region 400-533 nm, then the number of independent overlapping passbands covering this range is small (note that the figure below shows only every other SNAP filter for clarity)
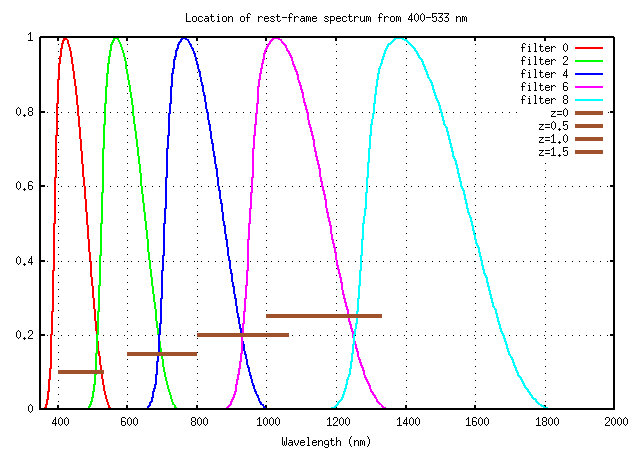
Looking at the figure above, we see that this region of spectrum falls (roughly) into filter 6 at z=1.5, and into filter 5 at z=1.0. That means that we would have only a single measurement delta_mag with which to compare two supernovae at these redshifts.
On the other hand, if we know the rest-frame spectrum over the wide region 400-900 nm, then the number of independent overlapping passbands covering this range is larger:
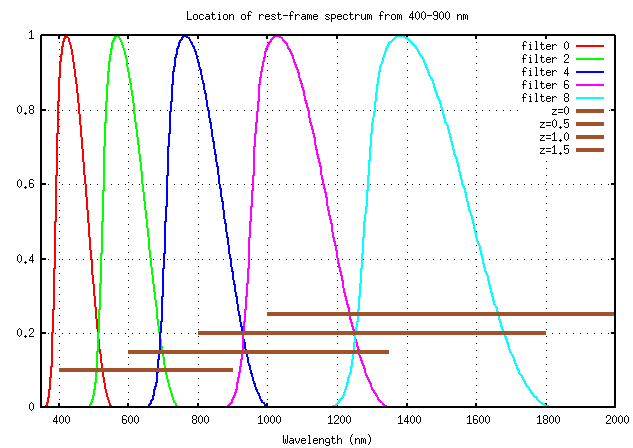
In this case, the known region of spectrum falls into filters 5, 6, 7 and 8 at redshift z=1.0, and into filters 7 and 8 at redshift z=1.5. That would provide 8 pairs of delta_mag for analysis, much more information than we would have in the first case.
The spectrum does not need to be calibrated in any absolute scale. That is, we do not need to know how many ergs per square centimeter per steradian per Hertz are emitted at 500 nm. However, each element of the input spectrum must be known relative to each other element: we do need to know the exact relative flux at 500 nm vs 501 nm vs 502 nm, etc. Any error in the shape of the spectrum will lead to systematic errors in the derived relative magnitudes and hence distances.