Waqas Bhatti gathered a nice, big chunk of data from the SDSS for tests of photometry.
Attached is the data for Field 418, Run 94 (Justin's second report). I used the following criteria:
SDSS PSF r mag from 14 to 25 Flags: NOT(SATURATED, BRIGHT, NOTCHECKED, DEBLENDED_AS_MOVING, BAD_MOVING_FIT, MAYBE_CR, MAYBE_EGHOST, BLENDED) and (BINNED1)
(Flag descriptions at: http://cas.sdss.org/runs/en/help/browser/enum.asp?n=PhotoFlags )
The stars fall within a box with rough limits 37.35 < RA < 37.51 and -0.21 < Dec < +0.01 The photometry comes from repeated scans of the celestial equator, some as part of the SDSS Supernova Survey. These scans were made over the past few years, with Julian Dates ranging from 2,451,075 (Sep 18, 1998) to 2,453,641 (Sep 27, 2005).
Here's a picture of the field, taken from the POSS-I plates, courtesy of Aladin.

I used my ensemble photometry package (with very minor modifications) to
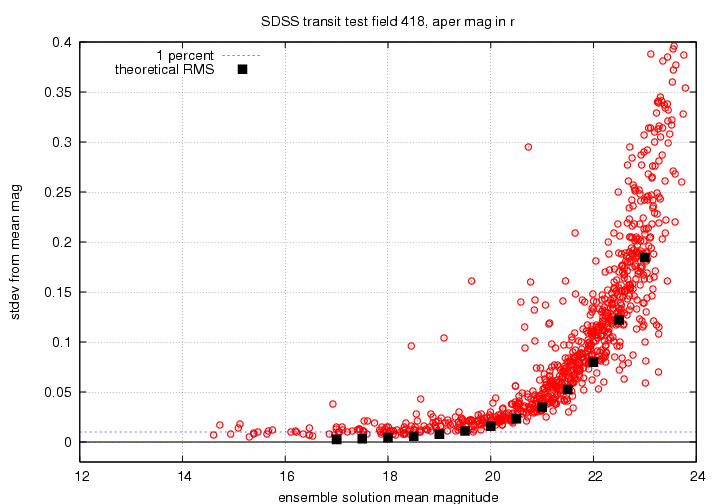
My primary tool for gauging the quality of a solution was the scatter-versus-magnitude relationship: if the scatter of most of the stars is relatively small, then the solution is good. Since stars at the bright end might be saturated, I looked at them carefully, and marked as "variable" any which showed a scatter larger than expected; these "variable" objects are not used to determine the photometry solution, but do appear in the output.
I will show the results for the g'-band, r'-band and i'-band photometry only in a series of graphs below. Each displays scatter from the ensemble mean magnitude on the vertical axis, and the mean ensemble magnitude on the horizontal axis. Note that the brightest stars tend to show elevated scatter (in some cases too high to appear on on the graph); almost all of these are, I believe, due to saturation. I show on each graph the level corresponding to a scatter of 0.01 mag = 1 percent. There are black squares showing the estimated RMS for stars, based on theoretical calculations of the telescope and filter throughputs, etc. from Gunn et al., AJ 116, 3040 (1998).
I will use only the "fiber" magnitudes, since we have learned that these aperture measurements are more stable from night to night than the PSF-fit magnitudes.
The first pass of the ensemble solution yields the following graph of "sigma-vs-mag":
Let's zoom in on the interesting regions.
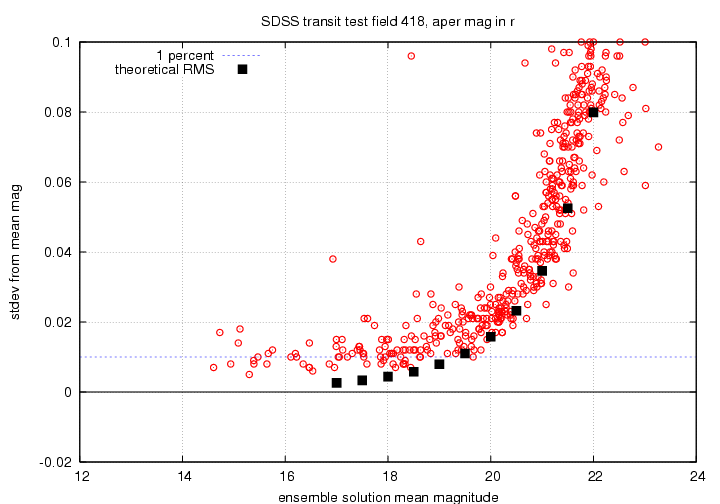
There are several features we can see in a glance:
There are a few outliers with scatter much larger than one would expect. Let's look at a few of them. The three outliers in the closeup figure are at roughly
A: rmag = 16.928, rsig = 0.038 37.39122, 0.66545 8658170690058453028 B: rmag = 18.454, rsig = 0.096 37.37436, -0.08688 8658170688984711242 C: rmag = 18.636, rsig = 0.043 37.43294, -0.58280 8658170688447840380I'll also include a "constant" star, one chosen at random which has a small scatter from the mean. Here are the light curves of these stars:
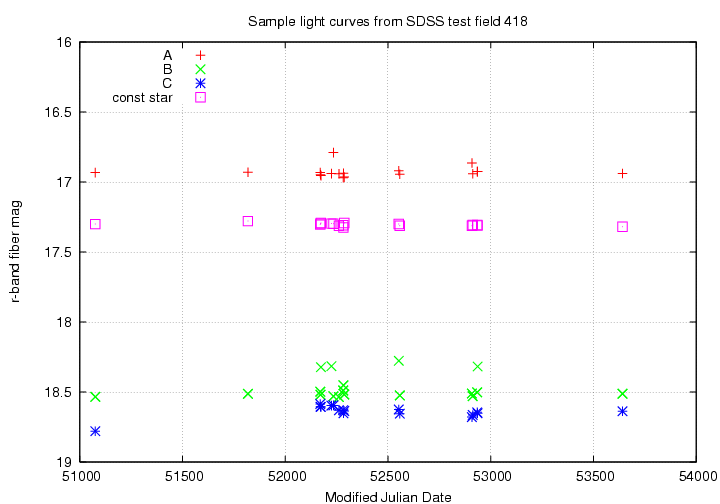
Based on this very small sample -- but also experience with other sets of photometry in the past -- I would note
The "sigma-versus-mag" plot is one way to look for evidence of variability. It may not be the best tool, especially for our purposes.
The first pass of the ensemble solution yields the following graph of "sigma-vs-mag":
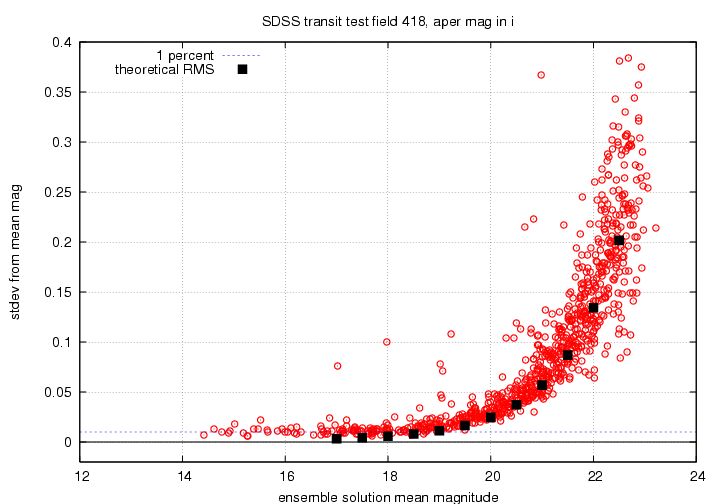
This shows the same behavior as the r'-band photometry. Fine.
Once again, I'll concentrate on the three stars which had higher-than-expected scatter in the r'-band photometry. I'll also include the same "constant" star, one chosen at random which has a small scatter from the mean. Here are the i'-band light curves of these stars:
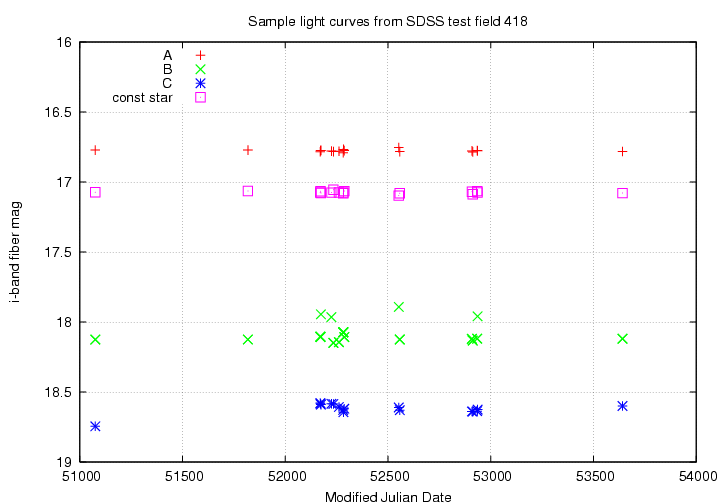
Aha. It turns out that one of our three variable candidates does NOT show any significant variability in i'-band.
--------------------------------------------------------------------------
A: imag = 16.777, isig = 0.008 37.39122, 0.66545 8658170690058453028
B: imag = 17.976, isig = 0.100 37.37436, -0.08688 8658170688984711242
C: imag = 18.618, isig = 0.034 37.43294, -0.58280 8658170688447840380
Star A looks constant in the i'-band, which suggests that its r'-band scatter was due to a single bad measurement. On the other hand, the scatter, and the detailed light curves, of stars B and C are similar in both passbands. We may then conclude that stars B and C may really be varying (though in different ways).
Well, I guess this was obvious :-)
The first pass of the ensemble solution yields the following graph of "sigma-vs-mag":
This shows the same behavior as the other passbands.
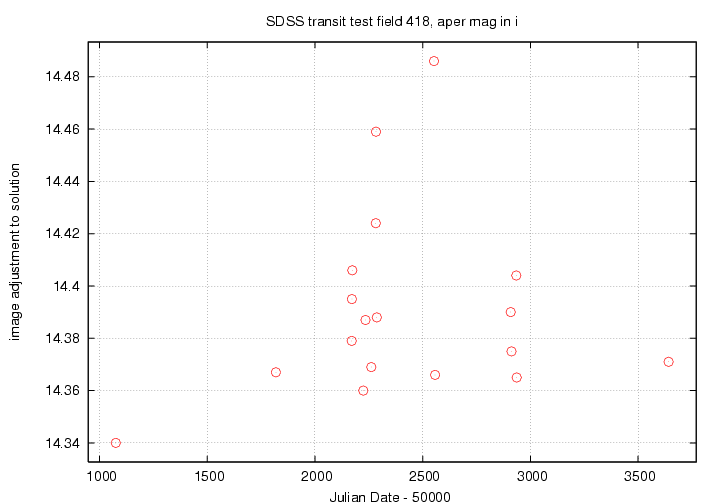
Another of the ensemble photometry method's results is the "adjustment" for each image (or each night): the amount by which all the measurements on that image (or night) should be shifted to bring them into agreement with the other images (or nights).
Let's look at the adjustment values for the ensemble solutions in r'-band and then i'-band. First, the r'-band result:
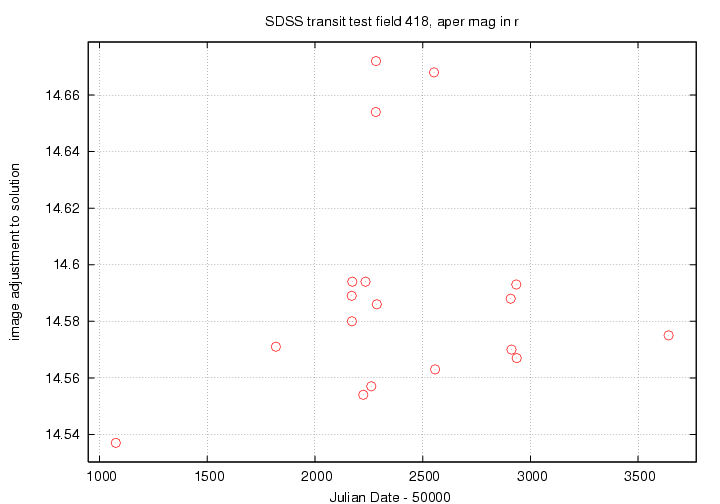
Now, the i'-band result:
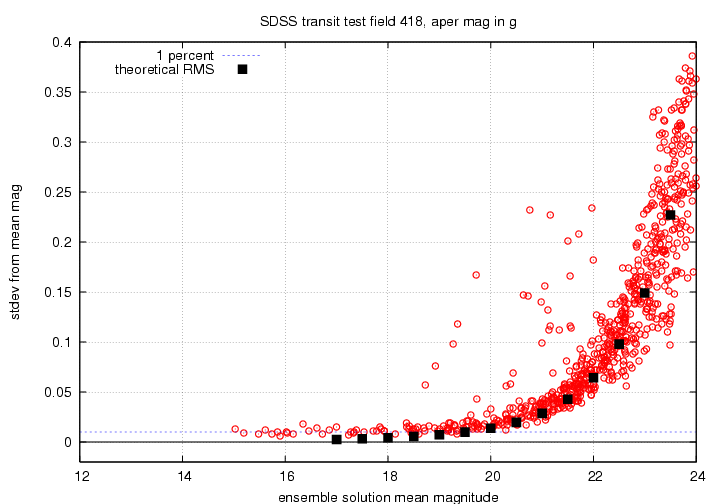
Finally, the g'-band result:
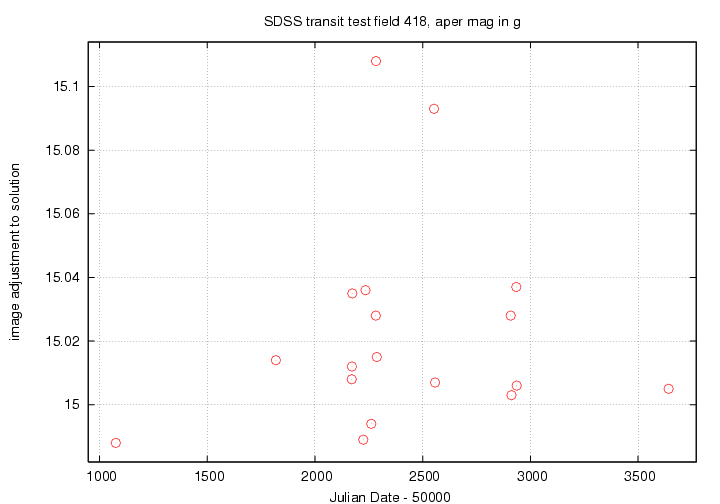
You can see similar patterns in all passbands. The big outliers are likely due to thin clouds. The long-term change from the first night to all the others may be due to gradual buildup of dust on the mirrors, or some long-term change in detector properties.
I provide below some of the output files from the ensemble solutions. The ".sig" files look like this:
0 13.193 0.158 0 0.25 35.32486 7.03099
1 11.360 0.073 0 -0.26 35.33325 6.72861
2 12.190 0.078 0 -0.75 35.33335 7.18730
3 13.695 0.137 0 -0.84 35.34351 6.66053
The columns in this file are
Below are files showing the full light curve of each star (well, actually, the values for all stars in a passband are gathered together in a single file). You can find the format of these files described in the ensemble package documentation; look at the section describing solvepht.out files.