
Worksheet to accompany this exercise
On July 4, 2010, UT, I used the RIT Observatory's 12-inch telescope to take pictures of Pluto. Over a period of several hours, it moved just a few arcseconds, barely enough to see in our images. Click on the image below to watch the animated collection -- can YOU find Pluto?
I returned to the same field on July 7, 2010, UT, and took another set of images. Once again, it _is_ possible to notice the motion of Pluto when looking at the images from this night alone, but it isn't easy.
However, if you compare an image from July 4 to one from July 7, you should be able to find Pluto pretty easily. Go ahead and give it a try -- just click on the image below to start "blinking".
Let's try to use this motion of Pluto to figure out how far away from the Earth it is. We'll use the following tools:
We'll also use a powerful technique which many scientists apply when they face complicated problems -- the method of successive approximations. In other words, we're going to start by making an assumption which we know is wrong, but only in order to get a first, rough estimate for the result; we can then use a more accurate model to refine the result. It may surprise you, but scientists do this sort of thing very often: adopting a view which they know can't be correct, just to get them started. Well, I do, anyway.
First, we must measure the distance Pluto appears to jump across the sky from July 4 to July 7. I've made a couple of figures to help you do that. There are two ways you can measure this angular distance. One way involves nothing but paper and rulers, but it may take a little while. The other method is quicker, but it requires you to use some sort of graphics-display program on your computer.


One way is to use the scales I've added to the figures below. Print out each figure, mark the position of Pluto with a dark pen, then place one on top of the other and hold them up to a light. You should be able to see the mark for Pluto on the bottom image through the paper of the top image. Place a mark at that location on the top image, so that you have marks for Pluto's position on both night on a single piece of paper. Then
The other way is probably quicker: use a good graphics-display program, such as Photoshop or Gimp, to display each image. Note the pixel position of Pluto on each image, and write it down. For example, you might write down (no, these aren't the right numbers)
July 4 X = 234 Y = 336 July 7 X = 651 Y = 399 ------------------------------------- difference 417 63
Then use the Pythagorean theorem to determine the number of pixels Pluto jumped from one image to another. Using my numbers (which, again, aren't correct),
Finally, you can convert pixels into arcseconds by multiplying by 0.9425:
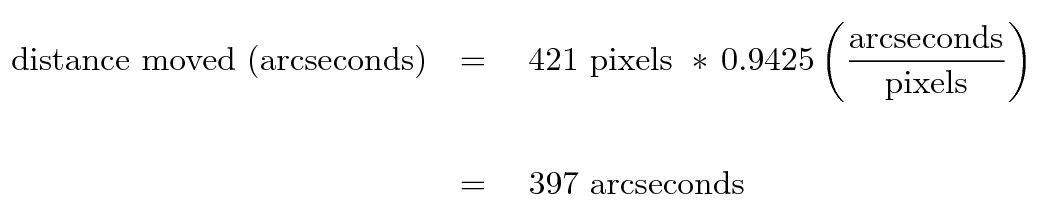
How did I figure out the conversion between arcseconds and pixels? I measured the positions of several stars in this image, in pixel units; next, I computed the distance between several of the stars, again in pixel units. Then I went to the Vizier on-line catalog archive and used the positions of those stars to compute the distances between them in arcseconds. The ratio of the distances in arcseconds to the distances in pixels gave me the conversion factor.
Remember, my example above is just to show you what to do; the numbers aren't correct. Your job is to measure the distance and perform your own calculation to find the distance moved by Pluto, in arcseconds.
Task A: How far does Pluto appear to jump from July 3 to July 7, in arcseconds?
Now, we all know that Pluto, like other bodies in the solar system, moves around the Sun in an elliptical orbit. However, the fact that both the Earth and Pluto are moving complicates our task of determining the distance between the two objects. So, to begin, let's pretend that Pluto doesn't move at all, but sits motionless in one place far, far from the Sun. Actually, that's not a terrible assumption, because Pluto does move around its orbit much more slowly than the Earth.
Over the course of the time between our two images (just a little over 3 days), the Earth moved some distance along its orbit around the Sun. We can look up the speed with which the Earth moves in its orbit around the Sun in many places; its speed is about v(Earth) = 30 km/sec.
The time between the first image, on July 4, and the second image, on July 7, was 3.04 days. How far did the Earth move during that time? You'll have to convert days into seconds to find out ...
Task B: How far, dE, does the Earth move between the two pictures, in km?
Now, the basic idea we'll use to find the distance to Pluto is called parallax: the apparent motion of an object when it is viewed from different locations. In this very simplified view, we look at Pluto from two locations which are -- as you have just calculated -- a long distance apart along the Earth's orbit.
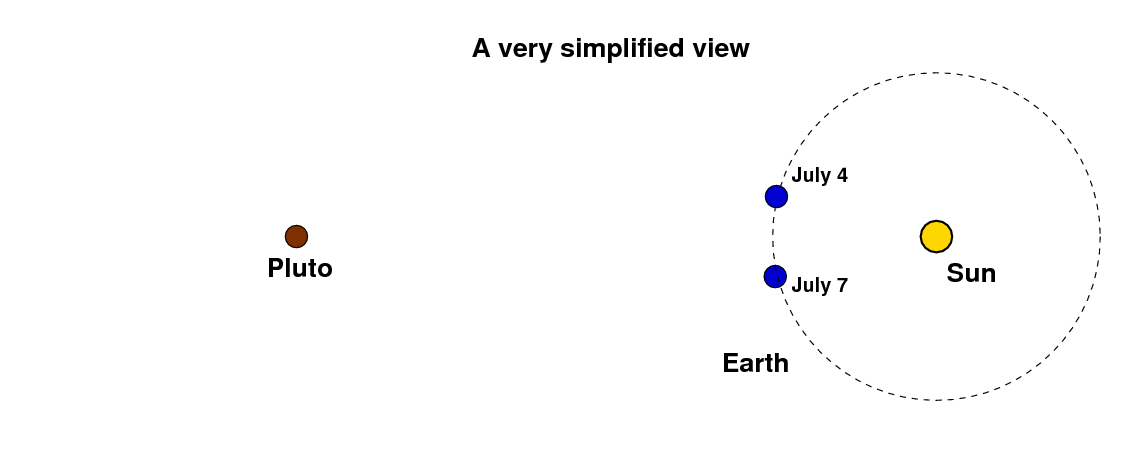
Because of our motion, it looks to us as if Pluto is moving relative to the stars which appear far behind it in the sky. On July 4, Pluto appears to be in front of the star labelled "A", but on July 7, it appears to be in front of the star labelled "B".
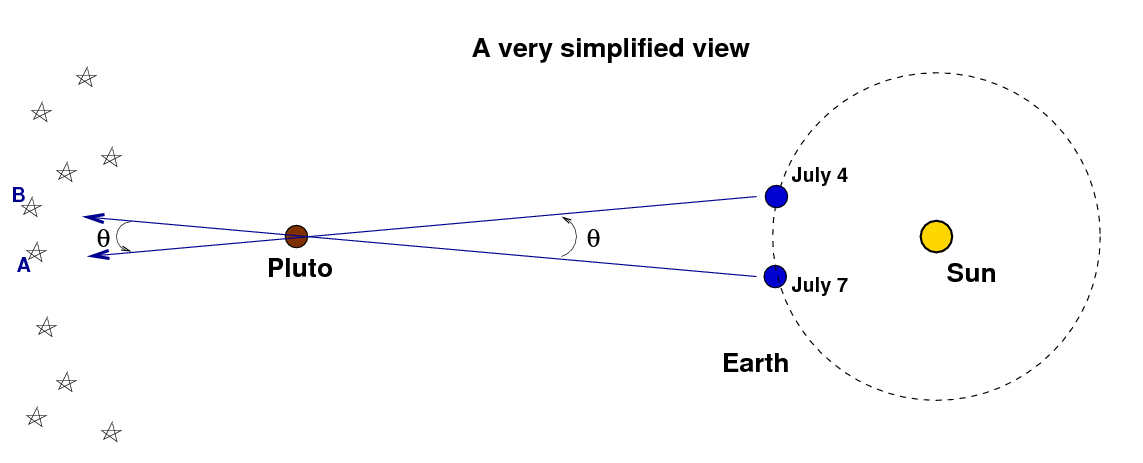
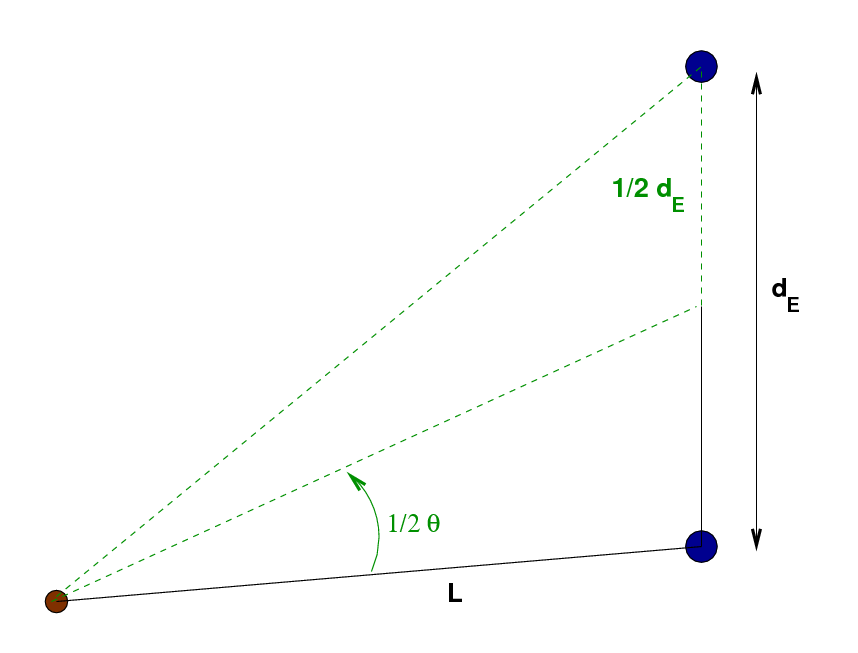
If we can measure the apparent angular motion of Pluto relative to the stars -- let's call that angle θ -- then we can figure out how far away Pluto must be. The key is to create a right triangle by splitting the triangle in our diagram in half, like this:
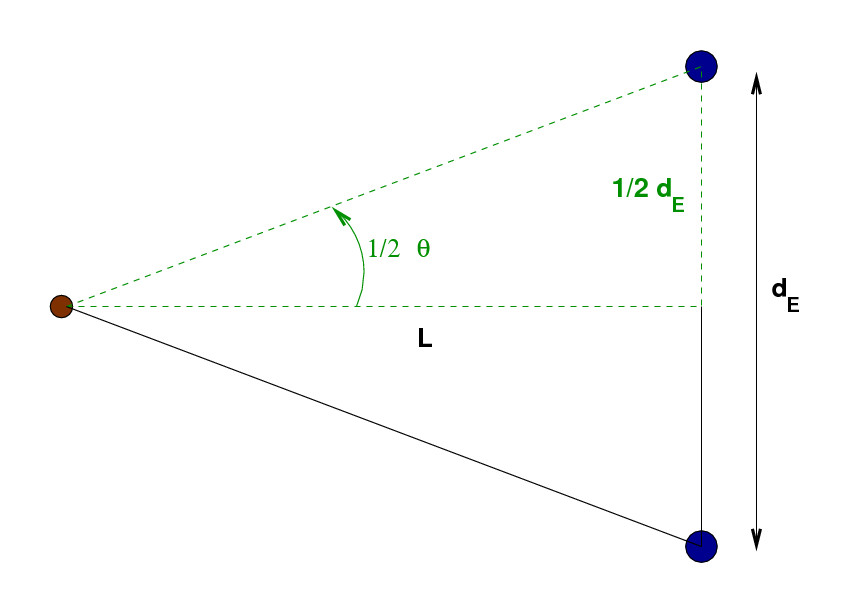
The upper half of this triangle, outlined in green dashed lines, is a right triangle. The angle at the skinny end, 1/2 θ, is half of the angular distance Pluto appears to jump, and the short side is half the distance dE travelled by the Earth in its orbit between the two pictures. The distance between Pluto and the Earth, L, can be calculated using trigonometry:
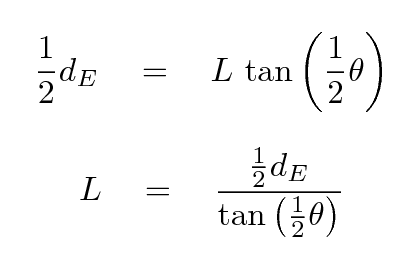
Before you get out your calculator, make sure that you convert your value for the angle θ Pluto appears to jump between July 4 and July 7 from arcseconds to degrees:

Okay, I think you are ready: use your value θ for the angular distance Pluto appears to jump, and the value you calculated above for the distance the Earth moves in its orbit, dE, to calculate the distance L from Earth to Pluto at the time I took my pictures.
Task C: What is your value for the distance L between the Earth and Pluto, in km?
I'm sure that you computed a very large number for this distance L. It's awkward to discuss and compare very big numbers, so let's turn it into a smaller, more handy number: instead of kilometers -- which are nice for distances between cities on Earth -- let's use Astronomical Units (AU), which are designed to measure distances in the Solar System. You can convert your value for the distance into AU like so:
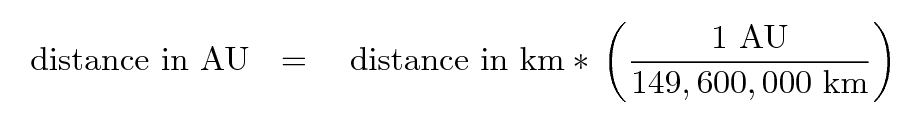
Task D: What is your value for the distance L between the Earth and Pluto, expressed in AU?
Astronomers know what the actual distance between Pluto and the Earth is. It changes from year to year due to the combined orbital motions of the two planets, but we can find the distance for any particular date and time by using the JPL Horizons ephemeris system. When I use this web site and request the distance for the date July 4, 2010, I am given the response 30.9 AU for the distance between Pluto and the Earth. How does your value compare to this actual distance?
When I went through all the steps described above to find the distance between the Earth and Pluto, I ended up with a value which was considerably larger than the actual distance. I'll bet you did, too. The mistake we made -- and we knew we were making a mistake -- was to assume that Pluto didn't move at all in the three days between the first and second picture. Of course, Pluto does move during that time ... but not by much, as this picture indicates.
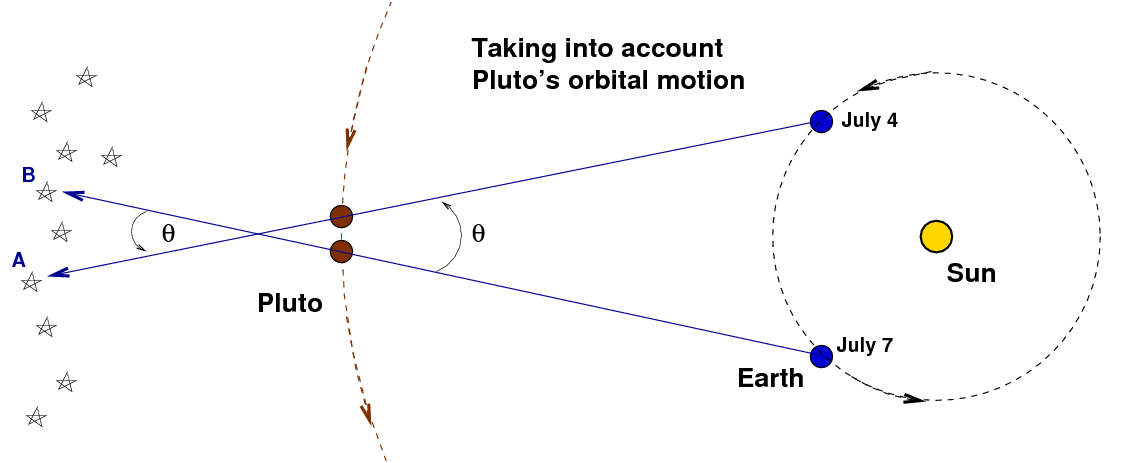
Pluto orbits the Sun in the same direction as the Earth, but it moves more slowly. Therefore, when we draw lines connecting the Earth with the apparent position of Pluto on the two days, those lines cross at a location a bit farther away from the Sun than Pluto itself. That's why our early calculations yielded a distance which was larger than the actual distance between the Earth and Pluto.
We can still use our measurement of the angle θ to find the distance to Pluto, but we need to do a little extra work. It will help to break up the distance L into two pieces: the distance L1 from the Earth to Pluto -- which is what we really want to know -- and the distance L2 from Pluto to the point where the two diagonal lines of sight cross.
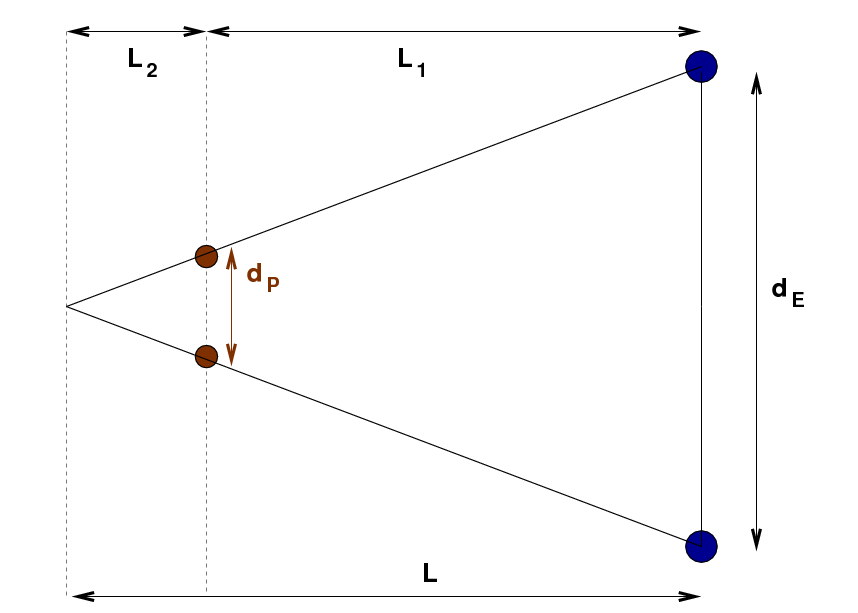
If we knew the distance Pluto moved during this three-day period, dP, then we could separate the total distance L into its two pieces, and we could find the distance L1 between the Earth and Pluto. Fortunately, a certain astronomer named Kepler discovered long ago that there is a mathematical relationship between the distance of an object from the Sun and the time it takes for that object to complete one orbit. We can use Kepler's discovery to figure out dP.
Kepler's Third Law of planetary motion states that the period of a body's orbit T is related to its distance from the Sun a in the following way:
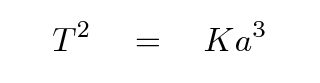
The constant K is the same for all bodies in the solar system. If we take the square root of both sides, we end up with a formula which gives T all by itself.
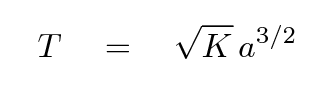
We'll use Kepler's Law to find a similar relationship for the SPEED of objects in their orbits around the Sun. If we assume that all the orbits are circles, then the distance an object has to travel around its orbit is 2πa, and the speed of the object is therefore
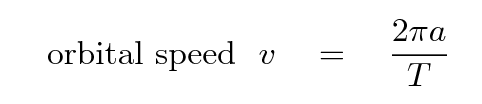
If we replace the T in this equation with its equivalent in the equation just above, we get
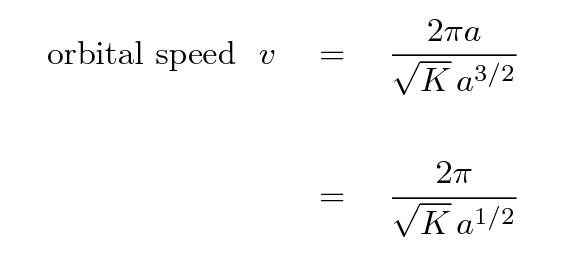
Evidently, the farther a planet is from the Sun, the larger its distance a, and so the SMALLER its orbital speed v.
We know the speed with which the Earth moves around the Sun: about vE = 30 km/s. We know the distance of the Earth from the Sun, aE = 1 AU. The distance from Pluto to the Sun, aP, is equal to the distance L from Pluto to the Earth, which you estimated earlier, plus the distance aE from the Earth to the Sun.

So, with all that information, you should be able to figure how fast Pluto moves:
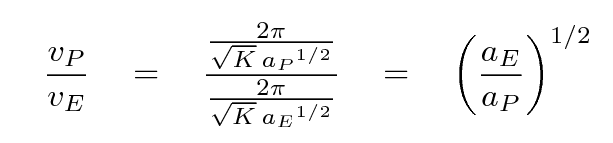
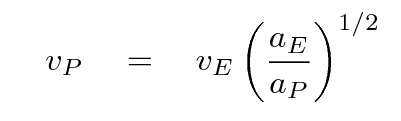
Task E: Use your first, rough guess for the distance between Earth and Pluto and the equation above to calculate the speed of Pluto in its orbit.
Both Pluto and the Earth move along their orbits for the same period between the two pictures: 3.04 days. Since you have at least a decent guess for the speed of Pluto now, you should be able to compute the distance it moves dP during this period.
Task F: How far, dP, does Pluto move during the period between the two pictures, in km?
We are ALMOST ready to compute a new, improved distance between the Earth and Pluto. Let's look at the simplified diagram again, but this time, add a little copy of the left-hand section of the big triangle.
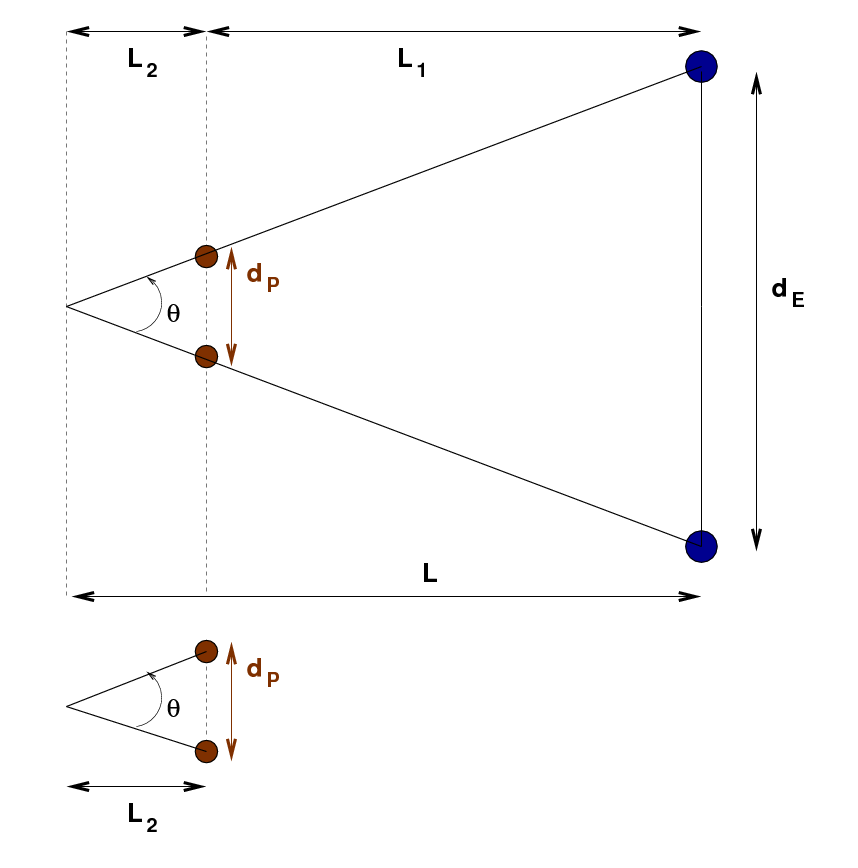
The big triangle and the little triangle are similar, which means that

You know all the values on the right-hand side of this last equation, so you should be able to calculate the distance L2 from Pluto to the point at the skinny end of the big triangle.
Task G: What is the distance L2 from Pluto to the skinny end of the big triangle, in AU?
Aha! That's the last piece of the puzzle! We can now improve our estimate of the distance from the Earth to Pluto; this time, we'll be including the motion of Pluto in our calculation.
You earlier made a rough estimate of the distance to Pluto, assuming that Pluto didn't move at all in its orbit, right? That rough estimate appears in the figure below as the distance L, from the Earth's orbit to the end of the skinny triangle.

That rough estimate turns out to be larger than the true distance, as this figure indicates. But now you have a good estimate for the extra distance L2 the triangle extends past the position of Pluto. Since you know L and L2, you can compute a new, improved distance between the Earth and Pluto:

Task H: What is your value for the improved distance L1 from the Earth to Pluto, in AU?
How does this new value compare with the actual distance of 30.9 AU?
When I went through this procedure, my improved distance between the Earth and Pluto was 29.8 AU, which is a bit less than the actual distance of 30.9 AU. Why was my answer incorrect? What was I doing wrong?
One reason the answer isn't correct is that we are using an OLD value for the distance between the Earth and Pluto to compute Pluto's orbital velocity; we ought to use the new, improved distance to compute Pluto's orbital velocity for Task E, and then use that better velocity to compute a better distance moved by Pluto, etc.
But the main reason that our answer is not quite correct is that we've made several assumptions, some explicit and some implicit, in order to simplify this whole problem.
Assumptions 1 and 3 are pretty good ones, but 2 and 4 are not: Pluto does NOT move in a circular orbit, and its speed is NOT the same everywhere along its orbit. Take a look for yourself at the diagram below, which shows the orbit of Pluto in red.
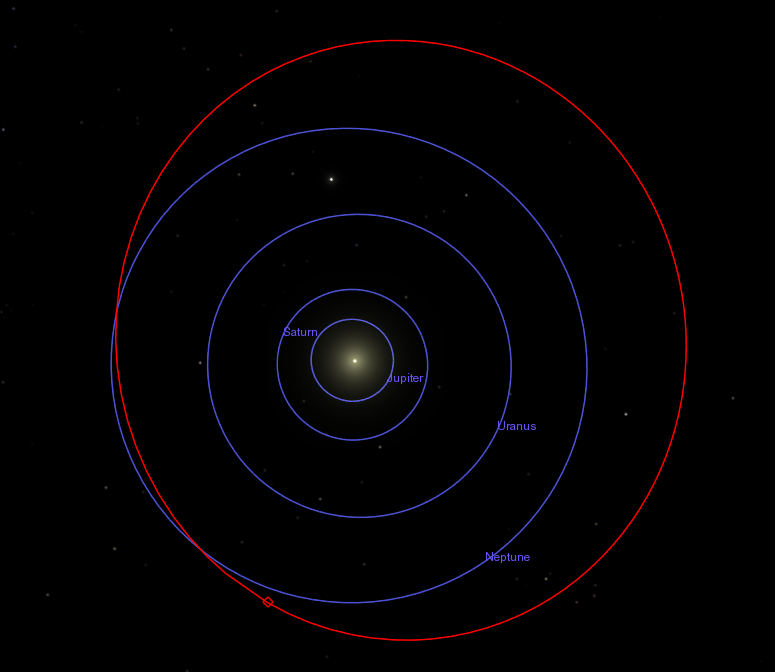
Image created by the most excellent
Celestia software.
Pluto's orbit is actually the most non-circular of the traditional planets. Its orbital speed varies quite a bit, being faster than average when Pluto is closest to the Sun and slower than average when Pluto is farthest from the Sun. When we applied Kepler's Third Law to compute Pluto's orbital speed, we calculated its average orbital speed -- not the speed it has right now.
Our assumption number 5, that the Earth was exactly in between the Sun and Pluto, is another mistake. The image below has a red diamond to indicate where Pluto was in its orbit on July 4, 2010. If you click on the image, you'll see a blinking animation which indicates the location of the Earth in its orbit on the same date. The Earth is not quite directly between the Sun and Pluto ...
Here's a closeup view showing the Sun (the little yellow circle) and the location of the Earth on July 4 and July 7, 2010 (red markers, with July 4 being the upper one). The green dashed line shows the direction of Pluto. As you can see, the Earth is just a little to the side of this line.
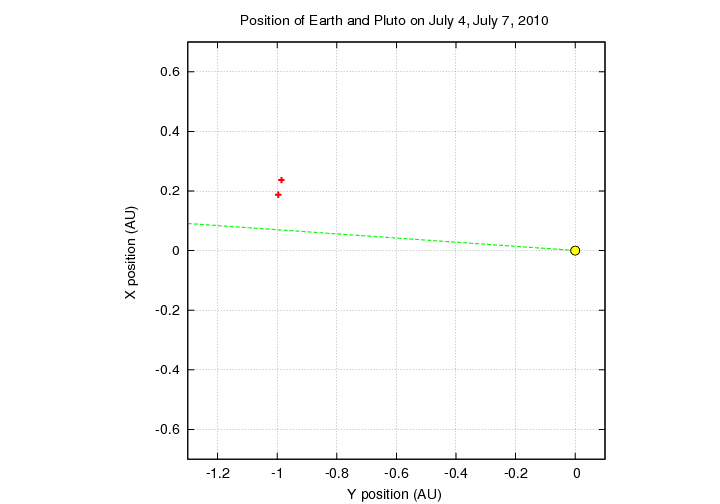
That means that the actual geometry of the situation looks like this: our triangles are skewed, and don't feature the perfect right triangles we need for those trigonometric formulae.
Finally, our assumption number 6, that the Earth's orbit and Pluto's orbit are in the same plane, is also not a very good one. Pluto's orbit (shown in red) is tilted by about 17 degrees relative to the Earth's orbit (one of the blue orbits), as you can see in the diagram below:

Now, it's not IMPOSSIBLE to include all these complicating factors when one calculates the distance between Pluto and the Earth; but it does make the problem much longer and more difficult. Our simplified version didn't take us too long, and it gave us an answer which is less than ten percent from the actual value. I'd call that a pretty good result!
Last modified 7/21/2010 by MWR.