Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Let's review the known properties of the universe at large, based on the early measurements of Hubble and other astronomers:
One simple way to explain these observations is to state that the universe is expanding. Or, more accurately, that on very large scales, space is expanding, and carry galaxies along with it like raisins in a loaf of bread.
Click on the picture above to watch the bread rise
Note that, from the point of view of ANY raisin, all other raisins are moving away: there is nothing special about the location of any particular raisin.
Note also that nearby raisins recede relatively slowly, while more distant raisins recede quickly.
Q: Does this mean that there is some force pushing
the distant raisins harder than the nearby ones?
No, there is no such force. There is no difference between the action of the rising bread at one location and the action of the bread in another location: it is puffing up equally fast in every place. The consequence of this sort of uniform expansion, however, is that more distant objects appear to be receding more quickly.
What can we say about the evolution of this expanding universe? Well, in the simplest case, if the ordinary laws of physics apply everywhere throughout the universe, then there is only one force which is important on these intergalactic scales: gravity. The gravitational attraction between galaxies and cluster of galaxies will oppose their motion away from each other. If the gravitational forces are strong enough, they may slow the expansion down to a complete halt, and even reverse the motion into a contraction.
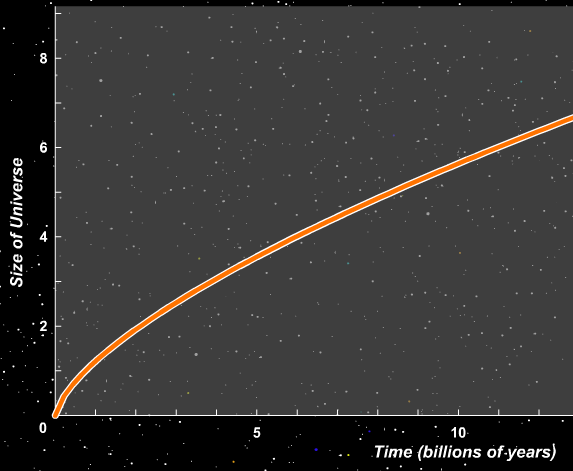
Click on the image above to run an applet showing
evolution of a simple universe
The fate of the universe depends on the amount of matter within it. Astronomers use the symbol "Omega" to describe the average density of matter in the universe on very large scales. As you can see by running the applet above with different values of Omega,
The critical density of matter required to permit the universe to continue expanding can be expressed two ways: in absolute terms, it's very roughly 10-26 kilograms per cubic meter, or about 6 hydrogen atoms per cubic meter. Astronomers often express this in a normalized way, saying that the critical density is by definition Omega0 = 1.
The $64,000 questions were: just what is the actual density of the universe, and how does it compare to the critical density?
Astronomers have tried to figure out the overall density of the universe for a long time. There are two main ways to calculate it.
The first method yields a relatively small matter density. If we were to spread out all the material into a uniform, very thin, gas, it would come to roughly one hydrogen atom per 5 cubic meters. That's nowhere close to the critical density.
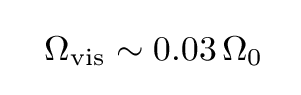
The second method indicates that there is much more mass in the universe than we can see directly: we sometimes call this inferred material dark matter. There appears to be very roughly ten times as much dark matter as visible matter! If we include the dark matter, then the overall density is about ten times higher, but still not high enough to close the universe:
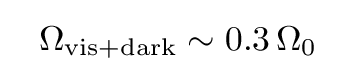
So, in the 1980s and early 1990s, the best available evidence suggested that the universe was open, and would expand forever.
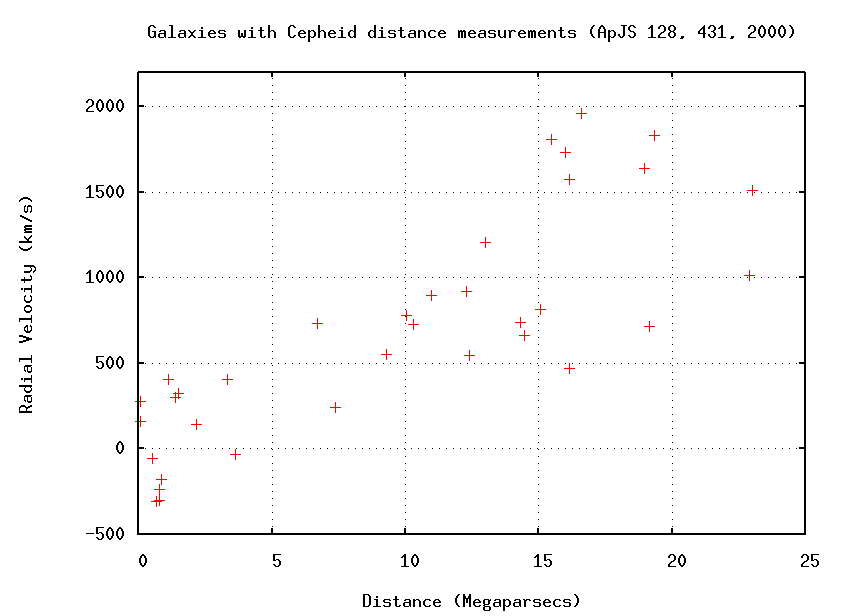
During the 1990s, several groups of astronomers devoted a great deal of time and effort to pushing the observations of distant supernovae to new limits. Using fainter and fainter Type Ia supernovae, they were able to measure the distances to galaxies farther and farther away. When they placed their new measurements of distance onto a Hubble diagram (together with the radial velocities of the host galaxies of the supernovae), they found something peculiar: the most distant supernovae did not lie in the expected location.
The figure below is a slightly modified version of the the normal Hubble diagram. Instead of placing the velocity on the vertical axis, it is here on the horizontal axis, expressed in terms of redshift instead of km/s; and, instead of putting distance on the other axis, we have a form of distance modulus.
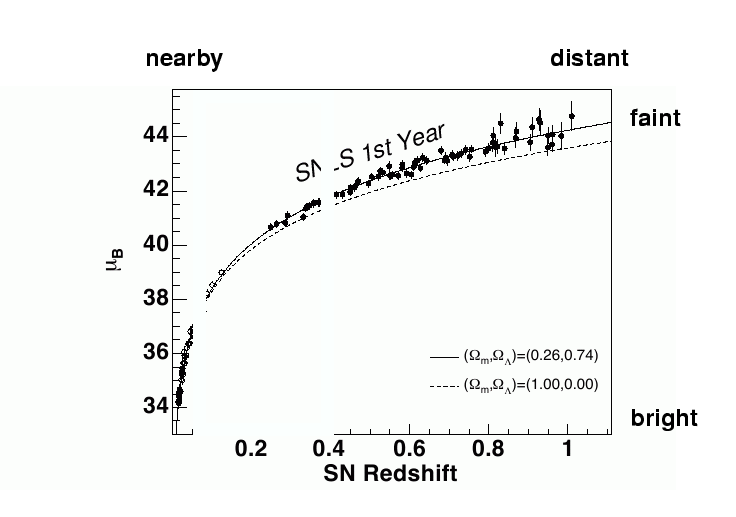
The lines you see drawn in this diagram show the expected locations for supernovae for particular models of the universe. If the universe contained only the visible matter we can see, plus the dark matter whose gravitational influence we can detect, the supernovae ought to lie close to the lower, dotted line. But they don't: if you average over the scatter, the most distant supernovae appear just a little bit FAINTER than we expect.
Why?
The reason is not clear or obvious. One way to explain it is to say that the supernovae which exploded very early in the universe are slightly fainter than the ones which explode today. We can't rule out this possibility, but we also don't have very strong independent evidence to support it.
Another possibility is that our model of the universe -- visible matter plus dark matter -- may be missing a critical piece. Theorists as far back as Albert Einstein realized that the equations of general relativity permit one to add a cosmological constant to the universe. This mathematical entity, often written with the Green letter lambda, Λ, is outside the bounds of our normal, everyday experience. If it exists, it has the property that it tends to "push space apart", or enhance the expansion of space on very large scales.
Click on the image below to run an applet which shows you how Λ can affect the evolution of the universe.
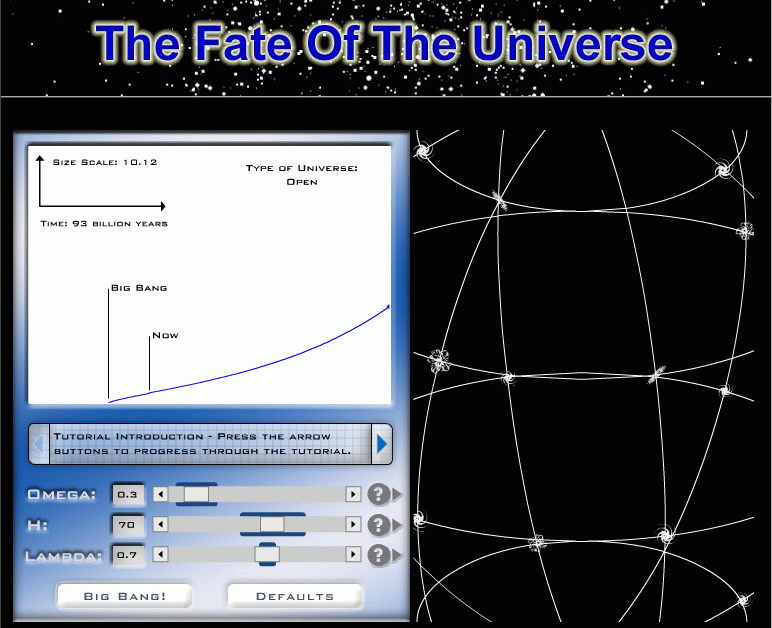
Thanks to
the Smithsonian Institution.
This cosmological constant has many names: it is sometimes called dark energy, though I don't understand why. Astronomers are currently trying several different methods to figure out what value this mysterious entity might have. One group of astronomers is planning to build a new telescope in space, called SNAP (SuperNova Acceleration Probe), which would spend several years searching for very distant supernovae and measuring their properties.
The search for Λ is one of the biggest efforts in astronomy today.
Several satellites -- COBE in the early 1990s, WMAP in the 2000s -- have measured the Cosmic Microwave Background, or CMB for short. These are radio waves which are relics from the very, very early universe, emitted by the hot gas when the universe was only about 300,000 years old.
After removing a number of contaminating sources, the CMB appears to have a lot of little spots: some a little hotter than average, some a little cooler.
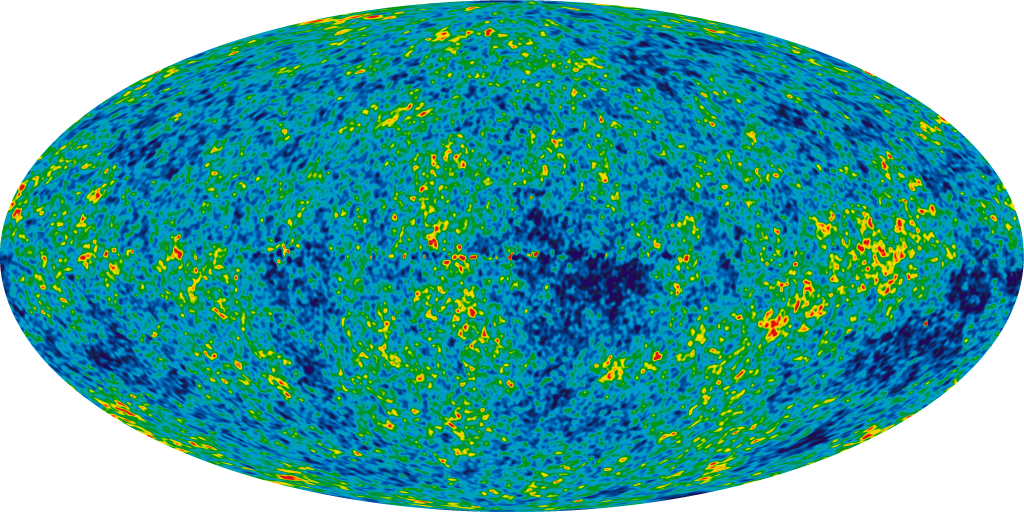
It turns out that the apparent size of these little spots tells us about the large-scale geometry of the universe. The spots were formed by slightly denser-than-average regions of the very early universe, when it was a very hot gas. We have a pretty good idea of the linear size (in meters) of the regions, based on our knowledge of hot gas. We think we know the distance to the regions, based on the time that they were formed, about 300,000 years after the Big Bang.
That means that we should be able to predict the apparent angular size (in degrees) of the spots on the sky.
It's easy to do if space is flat -- but not so easy if space is curved....
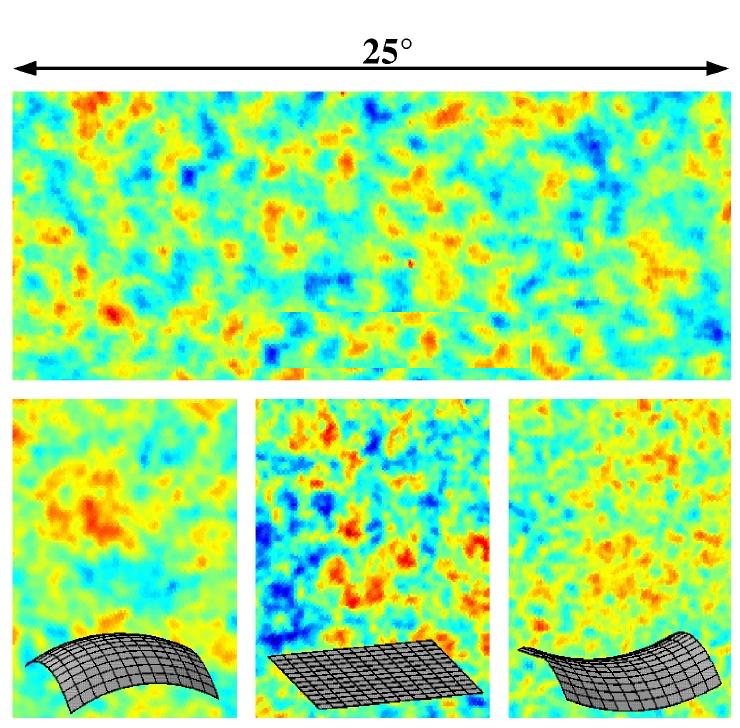
The current best measurements show that space is flat, to within the uncertainties. That means that the total mass-energy content of the universe must be exactly equal to 1.0, measured in an arcane set of units. But look at how it is distributed!
ordinary matter 0.04
dark matter 0.22
lambda 0.76
-----------------------------------
total 1.00
The universe is dominated by the cosmological constant, which tends to cause space to expand. The gravitational pull of the matter (ordinary plus dark) is not enough to restrain this expansion. As far as we can tell at the current time,
Future ---> unending expansion
---> loneliness :-(
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.