That just as there are other masses of matter than our globe, so there are among them other worlds than ours is an instant and inevitable inference from what we see about us. That we are the only part of the cosmos possessing what we are pleased to call mind is so earth-centred a supposition, that it recalls the other earth-centred view once so devoutly held, that our little globe was the point about which the whole company of heaven was good enough to turn. Indeed, there was much more reason to think that then, than to think this now, for there was at least the appearance of turning, whereas there is no indication that we are sole denizens of all we survey, and every inference that we are not.
That we are in some wise kin to all the rest of the cosmos, science has been
steadily demonstrating more and more clearly. The essential oneness of the
universe is the goal to which all learning tends. Just as Newton proved all
the
planets to obey a common force, the Sun; just as Laplace showed it to be
probable that we were all evolved from one and the same primal nebula; so
more recently the spectroscope has revealed unsuspected relationship betwixt
us and the stars. Matter turns out to be but common property; and the very
same substances with which we are so familiar on the Earth, iron, magnesium,
sodium, and so forth, prove present on those far-off suns that strew the
depths of space. Only in detail does everything differ.
So much for matter. As for that manifestation of it known as mind, modesty,
if not intelligence, forbids the thought that we are sole thinkers in all we
see. Indeed, we seldom stop in our locally engrossing pursuits to realize
how small the part we play in the universal drama. Let us consider for a
moment how we should appear, or, more exactly, not appear, could we get off
our world and scan it from without. If distance could thus reduce for us the
scale upon which the universe is fashioned to one we could take in, that on
which the Earth should be represented by a good-sized pea, with a grain of
mustard seed, the Moon, circling about it at a distance of seven inches, the
Sun would be a globe two feet in diameter, two hundred and fifteen feet
away. Mars, a much smaller pea, would circle around the two-foot globe three
hundred and twenty-five feet from its surface;
Jupiter, an orange, at a
distance of a fifth of a mile; Saturn, a small orange, at two fifths of a
mile; and Uranus and Neptune, good-sized plums, three quarters of a mile and
a mile and a quarter away, respectively. On this same scale the nearest star
would lie eight thousand miles off, and an average third-magnitude star at
about the present distance of our Moon; that is, on a scale upon which the
Moon should be but seven inches off, the average star would still be as far
from us as the Moon is now. Now when we think that each of these stars is
probably the centre of a solar system grander than our own, we cannot
seriously take ourselves to be the only minds in it all.
Probable, however, as extra-terrestrial life in general is, it is another
matter to predicate it in any particular case. Nevertheless, if it exist it
must exist somewhere, and the first place to scan is the place we can scan
best. Now the Moon appears to be hopelessly dead. Mars, therefore, becomes
of peculiar interest, and it was in hope of learning something on the
subject that the observations about to be described in this book were made.
Before proceeding, however, to an account of what in consequence we have
learned about our neighbor, a couple of misapprehensions upon the subject,--
not confined, I am sorry to say, wholly to the lay mind,--must first be
corrected. One of these is
that extra-terrestrial life means
extra-terrestrial human life. Such an inference recalls to my mind the
exclamation of an innocent globetrotter to a friend of mine in Japan once, a
connoisseur of Japanese painting, upon being told that the Japanese pictures
were exceedingly fine. " What! " the globe-trotter exclaimed in surprise,
"do the Japanese have pictures,--real pictures, I mean, in gilt frames?" The
existence of extra-terrestrial life does not involve "real life in
trousers," or any other particular form of it with which we are locally
conversant. Under changed conditions, life itself must take on other forms.
The next point is as to what constitutes proof. Now, between the truths we
take for granted because of their age, and those we question because of
their youth, we are apt to forget that in both proof is nothing but
preponderance of probability. The law of gravitation; for example, than
which we believe nothing to be more true, depends eventually, as recognized
by us, upon a question of probability; and so do the thousand and one
problems of daily life upon so many of which we act unhesitatingly and
should be philosophic fools if we did not. All deduction rests ultimately
upon the data derived from experience. This is the tortoise that supports
our conception of the cosmos. For us, therefore, the point at issue in any
theory is not whether there be a possibility of its being false, but whether
there be a probability of its being true. This, which is evident enough when
squarely envisaged, is too often lost sight of in discussing theories on
their road to recognition. Negative evidence is no evidence at all, and the
possibility that a thing might be otherwise, no proof whatever that it is
not so. The test of a theory is, first, that it shall not be directly
contradicted by any facts, and secondly, that the probabilities in its favor
shall be sufficiently great.
As to what constitutes sufficiency it is important to bear in mind one
point, namely, that the odds that a thing is true from the fact that two or
more witnesses agree on the same statement is not the sum of the odds that
each tells the truth, but the product of those odds.
Note (See Lacroix, Traite Elementarire des Probabilites, p. 220)
Therefore, if the
chances for the truth of a theory, in consequence of its explaining a
certain set of details, be three to one, and because of its explaining
another set,--for the purposes of argument unrelated to the first,--four to
one, then the chances in its favor from its explaining both sets are not
seven to one but twelve to one. If it explains a third set whose
independently resulting odds are of five to one, the chances in its favor,
from its explaining all three
sets, not twelve to one but sixty to one; if a fourth set be added, with
further odds of five to
one, the sum total from the four becomes not
seventeen to one but three hundred to one in favor of its being true. It
will be seen how rapidly the probability of the truth of a theory mounts up
from the amount of detail it explains. This law is to be remembered
throughout the coming exposition, for whatever the cogency of each detail of
the argument in itself, the concurrence of all renders them not simply
additionally but multiplicitly effective. That different lines of induction
all converge to one point proves that point to be the radiant point of the
result.
Thoroughly to appreciate, then, the physical condition of Mars, we must
begin at this beginning of our knowledge of the planet, since every detail
will be found to play its part in the final result. I shall therefore give
in a word or two
the general facts known about the planet, before taking up
the observations which make the subject matter of this book. The first of
these general facts is the path the planet describes about the Sun. Who
first found out that the ruddy star we call Mars was not like the rest of
the company about him we do not know ; possibly some, to fame unknown,
Chaldean shepherd alone with the night upon the great Chaldean plains. With
the stars for sole companions while his sheep slept, he must, as he watched
them night after night , have early recognized that they always kept the
same configuration. They rose and set, but they all rose and set together.
But one night he thought he noticed that one of them had changed its place
with reference to the rest. A few nights later he became sure of it. One of
the immovable had patently moved. That memorable though unremembered night
marked the birth of our acquaintance with the rest of the universe.
Whether the midnight pioneer was Chaldean or Assyrian or of some other race,
certain it is that to the Egyptians we owe the first systematic study of the
motions of this and of four other roving stars, and to the Greeks whom they
taught, the name by which we know them, that of planets, meaning merely
wanderers. Since then, as we know, many others of like habit have been added
to the list.
Now, from observations of the apparent places of a planet, it
is possible to determine the relative path of the planet in space as
compared with the path of the Earth. This Kepler did from observations of
Tycho Brahe's, and showed the wanderers to belong to a system of bodies, all
revolving about the Sun in various elliptic orbits, the Sun being at the
focus of each ellipse. He also found that the line connecting each planet
with the Sun passed over equal areas in equal times, and thirdly, that the
squares of the times were as the cubes of the major axes of the orbits. From
these three "laws" Newton deduced the fact that the force controlling the
planets was directed toward the Sun, that it varied inversely as the square
of the distance, and that it was the same in origin for all. This is the
so-called law of gravitation, and this is the way in which it was
discovered. We do not yet know why gravity so acts, but it is interesting to
note that it follows the simple law of geometrical expansion, diminishing in
exact ratio to the space it fills, just like electricity or light. It may,
therefore, also be a wave motion.
Thus all the wanderers proved to be associated in common dependence on the
Sun, and among the members of the solar family thus recognized Mars was
found to hold the position next exterior to the Earth, and the path he
followed
in his circuit of the Sun to be situated with regard to the
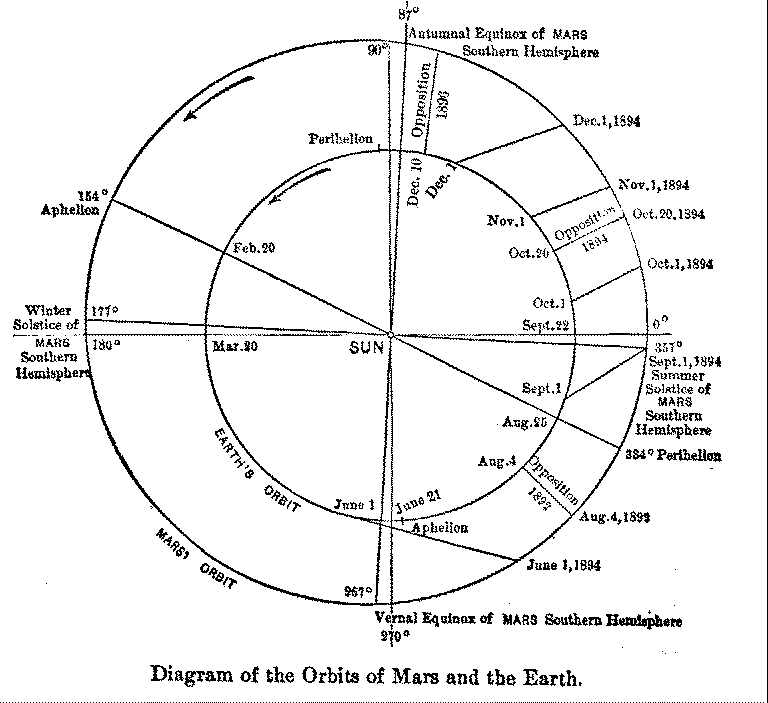
Earth's as in the following diagram.
On consulting the diagram we shall at once perceive why it is that every
fifteen years Mars becomes so unusually bright as to seem, to one who has
not kept track of him, a new and startling star. His orbit, it will be seen,
is an ellipse of some eccentricity, and deviates in consequence considerably
from a circle. The point marked Perihelion denotes the point where the
planet is nearest the Sun; the point marked
Aphelion, the point where the
planet is the most remote from the Sun. In like manner the points marked
Perihelion and Aphelion on the inner circle show the corresponding points of
the Earth's orbit, which is much more nearly circular. Now as the two
planets revolve in different periods of time, Mars taking 686.98 of our days
to complete his circuit, and the Earth 365.26 days to complete hers, the one
planet will overtake the other only once every two years and two months or
so. Meanwhile they are at great distances apart. But even when they do meet,
they do not always meet equally near. For the one orbital period is not an
exact multiple of the other, and as the orbits are both ellipses, it is
evident that these meetings of the two planets will occur at different
points of their orbits, and, therefore, at different distances. If the
meeting occur when Mars is in perihelion the planets approach one another
within 35,000,000 miles; if in aphelion, only within 61,000,000 miles.
But even this difference in distance does not measure the full extent of the
variation in brilliancy. As the brightness of an illuminated body varies
inversely as the square of its distance from the source of light, and as the
total amount of light it reflects to an observer varies inversely as the
square of his distance from it, it makes every difference in the apparent
brilliancy
of a body how the body is situated, both with regard to the
source of light and with regard to the observer. Now it so chances that at
the meetings of Mars with the Earth these two factors attain their maximum
effects nearly together, and similarly with their minimum. For at the times
when we are closest to Mars, Mars is nearly at his closest to the Sun, and
reversely when we meet him at the opposite part of his orbit. It thus comes
about that at some meetings,--oppositions, they are called, because Mars then
is in the opposite part of the sky from the Sun,--the planet appears four and
one half times as bright as at others. Here, then, we have the explanation
of the planet's great changes in appearance, changes so great as to deceive
any one who has not followed its wanderings, into the belief that it is some
new and portentous apparition.
Important as is the ellipse in which Mars moves with regard to his
visibility by us, it is considerably more important as regards the physical
condition of the planet itself. For the Sun being situated at one of the
foci of his orbit, the motion of the planet sweeps him now near to, now far
from that dispenser of light and warmth; and the amount of both which the
planet receives varies just like gravity with his distance from their
source. Now the eccentricity of the orbit of Mars is such that
when nearest
the Sun his distance is 129,500,000 miles, when at his mean distance
141,500,000 miles, and when most remote 154,500,000 miles. The proportion
of light and heat he receives respectively is therefore roughly as 16 to 20
to 24; or half as much again at certain times as at others.
So much in our knowledge of Mars is pre-telescopic. Men might have and
practically did learn this much without ever seeing the planet other than as
a point of light. Its orbit was tolerably accurately known and could have
been known still more accurately without telescopic aid; not so, until we
become much more nearly omniscient than we at present are, the planet's
self.
The relative plan of the solar system can be learned with great accuracy
from observations of the motions of its members; not so easily learned is
the scale upon which it is constructed. Although the former is intrinsically
a very complicated, the latter a very simple problem, two characteristics of
the actual system make it possible to solve the former much more nearly than
the latter. One of these characteristics
is the fact that the distances
between the masses which compose the system are very much greater than than
dimensions of the masses themselves, of quite a higher order of magnitude.
The diameters of the planets are measured by thousands of miles, the
distances between them by tens of millions. The second characteristic
consists in the approximately spherical shape of the planets themselves, and
in the fact that by a mathematical consequence of the actual law of
gravitation a sphere acts upon any outside body as if all its mass were
concentrated at its centre, a most interesting peculiarity not true under
many other supposable laws. These two facts very materially simplify the
problem of the motions of celestial mechanics.
But just as the first of these peculiarities helps us to comprehension of
the relative dimensions of the solar system, so does it hinder us in
determining its actual dimensions. For this determination depends upon a
problem in celestial surveying, the finding the distance to a body by
measuring the angle it subtends from the two ends of a base-line. Now, as
unfortunately we cannot get off the earth for the purpose, our base-line is
at most the diameter of the earth itself, and as the distance to the other
body immensely exceeds our own size, the angle to be measured becomes so
excessively small as
to be very difficult to determine with accuracy.
Fortunately this is matter chiefly of theoretic regret, as we now know the
actual sizes to within a degree of exactness practically sufficient for
most purposes but perturbations; to within about 1/300 part of the whole,
so far as our ultimate measure is concerned, the distance we are off from
the Sun.
A good idea of the method and some appreciation of the difficulty involved
in it can be got by considering a precisely similar case, that of
determining the distance of a spire a mile and three fifths away by shutting
first one eye and then the other and noting the shift of the spire against
its background. It is needless to add that without telescopic aid the
determination is impossible, and that it is exceeding difficult with it.
Nevertheless, from the distance of the Sun determined in this manner, we
find from measurements of the apparent disk of the planet made at Flagstaff
that Mars is about 4,215 miles in diameter. This makes his surface a little
more than a quarter that of the Earth and his volume about one seventh of
hers.
The next point to find out is his mass, that is, the amount of matter he
contains. This is very easy to determine when a planet has a satellite, and
very difficult to determine when
a planet has not. The reason is this: the
mass of a body is known from the pull it exerts, inasmuch as this pull
depends, by the law of gravitation, upon its mass and the square of its
distance. If then we know the pull and the distance from which it is
exerted, we can find the mass. Now we gauge the pull from its effects in
causing some other body to move. By measuring, therefore, the motion of this
other body, we learn the mass of the first one. To get this accurately the
motion must be large enough to admit of satisfactory measurement in the
first place, and be as uncomplicated with motions due to pulls of other
bodies as possible, in the second. As each body pulls every other, and it is
only their relative displacement we can measure, as we have no foothold in
space, even the case of only two bodies presents difficulties of
apportionment. We can learn the aggregate mass of the two, but not the
separate mass of either alone unless it so happen that the mass of one is so
insignificant compared with the other that the mass of that other may be
taken as the mass of both. Now this is substantially realized in the case of
the solar system. Owing to the greatly disproportionate size of primary and
secondary bodies in it, the great size of the Sun as compared with that of
any of the planets, and the great size of the planets as compared with their
satellites
(with the exception of the Moon, and she, fortunately, is an only
child), the determination of the mass of the smaller by measurement of its
motion about the larger,--as if only the pair of bodies under consideration
existed, and the mass of both were concentrated in the greater of the two,--
is very nearly exact. Inconsequence each planet discloses with some accuracy
the mass of the Sun, but tells next to nothing about its own mass; and in
the same way each satellite reveals the mass of its primary. The Mass of a
planet possessing a satellite is, therefore, easy of determination. Not so
that of one which travels unattended. The only way to obtain its mass is
from the perturbations or disturbing pulls it exerts upon the other planets,
or upon stray comets from time to time, and these disturbances are, by the
nature of the case, of a much smaller order of magnitude, to say nothing of
the fact that all act coincidently to increased difficulty of
disentanglement. The practical outcome of this in the case of Mars was that
before his satellites were discovered the values obtained for his mass
ranged all the way from 1/3,700,000 to 1/2,500,000, of the mass of the Sun,
or, in other words, varied fifty per cent. His insignificant satellites,
however, and just because they are insignificant, have made it possible to
learn his mass with great exactness. It turns out to
be 1/3,093,500 of that of the Sun, or 10/94 of that of the Earth.
Knowing his mass, we know his average density, since to find it we have but
to divide his mass by his volume. It proves to be 72/100 of that of the
Earth. We also learn the force of gravity at his surface, inasmuch as this
is directly as his mass and inversely as the square of his radius. It comes
out 38/100 of that of the Earth. In consequence, all things there would
weigh but 38/100 of their weight on earth; a man, for example, weighing 150
pounds here would weigh but 56 pounds if transported to the surface of Mars,
and all manual labor would be lightened threefold.
So soon as the planet was scanned telescopically, he was seen to present a
disk, round at times, at other times lacking somewhat of a perfect circle,
showing like the Moon when two days off from full. Such appearance visibly
demonstrated, first, that he was not a self-luminous body, and secondly,
that he revolved about the Sun outside of the Earth. A glance at the diagram
of the orbit will make the latter point clearer. If we draw a line from the
Sun to the centre of Mars and pass a plane through the planet perpendicular
to this line and to the plane of his orbit, this plane will divide the
illumined half of him from the unillumined half. If now we draw another line
from any point
of the Earth's orbit to Mars' centre, and pass a plane
similarly perpendicular to that, it will cut off the hemisphere we see at
any moment from the one we do not. As the two lines do not in general
coincide, it will appear that in certain positions, in fact in all but two,
Mars must present to us a face partly steeped in daylight, partly shrouded
in night; in short, that he shows gibbous like the Moon when she is between
the half and the full. This accounts for the look of the drawings made
during June, 1894, in which from a seventh to a sixth of the disk is wanting
on the left.
By drawing lines from his centre to more than one position
occupied by the Earth it will be seen that this lacking lune reaches a
maximum when the Earth as viewed from Mars is at extreme elongation from the
Sun, and that the amount of the phase at such time exactly equals the number
of degrees of this elongation. For example, on the sixteenth of last June
the lacking lune amounted to 47 degrees, that is, the Earth was then evening star
upon the Martian twilight skies at an angular distance of 47 degrees from the Sun,
about what Venus seems to us at her extreme elongation. In fact, to Mars we
occupy much the same astronomical position that Venus does to us.
To Huyghens we owe the first really important
telescopic observation upon
the planet. On November 28, 1659, at 7 P.M., he made the first drawing of the
planet worthy the name, for on it is the first identifiable feature ever
made out by man on the surface of Mars. This feature is the Hourglass Sea,
now more commonly known as the Syrtis Major. The accompanying cut of it is
reproduced from Flammarion.
If the dark patch in it be compared with the markings in the other pictures
of the planet, shown later in this book, it will be seen that the patch can
be none other than the Hourglass Sea.
Now, innocent as it looks of much detail, Huyghens' drawing is perhaps the
most important one of Mars that has ever been made. For, from his
observations of the spot it depicts at successive dates, he was able to
prove that Mars rotated on his own axis, and to determine the time of that
rotation, about 24 hours. As he subsequently came to doubt his results, the
honor of the discovery rests with Cassini, who, in 1666, definitely
determined that the planet rotated in 24 hours 40 minutes. Thus was it
first learned that Mars had a day, and that its length was not far from the
length of our own.
The importance of these earliest pictures of Mars has not lapsed with the
lapse of time. By comparison of this and other early drawings with modern
ones, has been deduced a very accurate value of the length of the Martian
day (its sidereal day), a determination accurate to the tenth of a second.
It amounts to 24 hours, 37 minutes, 22.7 seconds. Our sidereal day, that is,
the day reckoned by the stars, not by the Sun, is roughly 23 hours, 56
minutes; so that the Martian day is about 40 minutes longer than our own.
The result is not given here closer than the tenth of a second, because the
Flagstaff observations have shown that the value of the length of the
Martian day hitherto accepted is probably a trifle too small.
From the discovery of the rotation followed the approximate position of the
planet's poles. Round about the poles so determined appeared two white
patches, the first study of which we owe to Maraldi. They are the planet's
polar caps. They are to be detected with the smallest modern telescope.
The apparent position of the planet poles as presented to the Earth gives
the tilt of the planet's axis to the plane of its orbit. It turns out to be
about 25 degrees. This is very nearly the same as the Earth's axial tilt to the
plane of
her orbit, which is 23 degrees 24'. As the inclination of the axis to the
plane of the orbit determines the seasons, we see that not only has Mars its
spring, summer, autumn, and winter, but that these are not very unlike our
own.
It is not uninteresting to inquire in what the difference consists. The
slight difference of tilt in the Martian axis would slightly extend the
breadth of the tropical and the polar regions at the expense of the
temperate ones, and thus accentuate the seasons, but the chief seasonal
contrast between Mars and the Earth would come in consequence of the much
greater eccentricity of Mars' orbit. For the more eccentric the ellipse, the
greater the variation in the planet's velocity at different parts of it,
inasmuch as the Sun pulls the planet toward himself with a force depending
on his distance. The less this distance, the greater the angular velocity.
But the angular velocity determines the length of the seasons upon a planet
whose pole of rotation is tilted to the plane of its orbit, like the Earth
or Mars. The greater the eccentricity of the ellipse, therefore, the greater
the difference in the length of the seasons. In the case of the Earth the
difference is about eight days, winter in the northern hemisphere being
eight days shorter than summer. In the case of Mars, owing to the much
greater eccentricity of his orbit combined with his longer
period, the
difference amounts to 74 days. In one hemisphere winter is long and cold,
summer short and hot; in the other winter and summer interchange. Owing to
the present position of the line of apsides, the line connecting the points
of Mars' nearest approach to and farthest recession from the Sun, the former
hemisphere happens to be the southern one; the latter, the northern. The
lengths of their respective seasons are as follows:--
In the northern hemisphere, winter lasts 147 of his own days; spring 191
days; summer, 181 days; autumn, 149 days; while in the southern hemisphere,
winter lasts 181 days; spring, 149 days; summer, 147 days; autumn, 191 days.
Curiously enough, an analogous distribution of heat and cold occurs also at
the present time in the case of the Earth; its axis and line of apsides
holding the same relation to each other that the Martian ones do. This
similarity of aspect is, as we shall see later, apparently very curiously
reproduced in certain peculiarities of the surfaces of the two planets. But
with Mars the result is much more marked on account of the greater
eccentricity of his orbit, which is .0931 as against the Earth's .0168.
As even under these exaggerated conditions his two polar regions show much
alike, modern theories about our glacial epochs are considerably shaken.
The last of the preliminary points to be taken up is the form of the planet.
Consideration of it makes in some sort a bridge from the planet's past to
its present. For its deviation from a perfect sphere tells us something of
its history.
Between the shapes of the large planets, Jupiter, Saturn, Uranus, and
probably Neptune, and those of the small ones, Mercury, Venus, the Earth,
and Mars, there is a striking dissimilarity, the former being markedly
oblate spheroids, the latter almost perfect spheres.
Into the cause of this, very interesting as it is, we have not here space to
go. The effect, however, is so noticeable that while the most casual glance
at the disk of Jupiter will reveal its ellipticity, the most careful
scrutiny would fail to show Mars other than perfectly round.
Nevertheless, the planet is slightly flattened at the poles. Measures have
repeatedly been made to determine the extent of this flattening, with
surprisingly discordant results, most of the values being much too large.
Observations at Flagstaff during this last opposition have not only shown
that most of the values were too large, but have revealed the cause of their
discrepancy. There turns out to be a factor in the case, hitherto
unsuspected, whose presence proves to be precisely such as would cause the
observed variations in measurements. It not only accounts for the fact of
discrepancy, but for the further fact that the discrepancies should usually
be on the side of an increase of the apparent polar flattening. This factor
is the recognition of a perceptible twilight upon the planet, not only of
enough account to be visible, but to have been actually measured, quite
unconsciously, by Mr. Douglass, and disclosed only when the measures came to
be compared with each other. Of this I shall speak more at length when we
reach the subject of atmosphere. Here it is only necessary to say that the
presence of a twilight fringing the surface of the planet would have the
effect of increasing the apparent size of the equatorial diameter at all
times, but to a different degree at different times, and almost always more
than it would the polar one. In consequence, the polar flattening, which is
the ratio borne by the difference of the equatorial and polar diameters to
the equatorial diameter, would be seemingly increased.
The value of Mr. Douglass' measures is heightened by a certain happy event
of an unprecedented nature,--the first observed disappearance of the polar
cap, and that at the very time the most important measures were made. The
presence of the polar cap enters as a disturbing element into measures of
the planet's disk, on account of the increased irradiation it causes at the
extremity of the polar diameter,
which makes the polar diameter measure more
than it otherwise would. For the polar cap is the most brilliant part of the
disk; and for the same reason that any bright body seems larger than a dark
one of the same size, it dilates the planet unduly in that direction. The
resulting effect is further complicated by the fact that the polar cap is
eccentrically situated with regard to the pole of rotation, as we shall see
later; and as the pole is tilted, the cap is sometimes on the edge of the
disk and the irradiation in consequence large, and sometimes well on the
disk itself where its irradiation is little or nothing. As the amount of
its magnifying effect is not accurately known, there enters with it an
unknown error. Now, last autumn Nature herself kindly eliminated this source
of error.
The measures made by Mr. Douglass are thus entitled to special regard, not
only because of their number (a great many of them were taken), but chiefly
because Nature made the disturbing influence of the polar cap nil. When, in
addition, the twilight arc is allowed for, the measures show a most
satisfactory accordance and give for the value of the polar flattening 1/190
of the equatorial diameter.
Now, it is interesting that this value should receive corroborative support
from two quite different directions. The first of these is that 1/190 is
just about the flattening which would
result from the most probable
supposition we can make as to the past history of the planet. To show this
we may take the case of the Earth. Investigations along several different
lines all result in showing that the polar flattening of the Earth is almost
exactly such as would result in a fluid body whose density from surface to
centre increased according to the pressure and temperature of our Earth in
the past, and which rotated with its present angular velocity. In the case
of Mars, Tisserand has shown that the polar flattening under the influence
of his present rotation would, if the increase of density in his strata were
similar to the Earth's, be 1/227 of his equatorial diameter. If, on the
other hand, his mass were homogeneous, his polar flattening would be 1/178.
Now, in a fluid condition a body could not remain homogeneous, owing to the
pressure exerted by the outer strata upon the inner ones, unless the matter
of which it was composed were rigorously incompressible, which is certainly
not the case with the Earth, and with quite equal certainty not the case
with Mars. On the other hand, the increase of density from surface to centre
is undoubtedly less in Mars than in the Earth, since the pressure depends
upon the mass and the Earth's mass is nearly ten times that of Mars.
Consequently, from this cause, the polar flattening should be somewhere
between 1/178 and 1/227,
not far therefore from the value found above, 1/190.
The second bit of corroborative testimony comes from the behavior of the
satellites of the planet. Unlike a sphere, a spheroid acts unequally upon
a body revolving about it in an ellipse inclined to its equator. The ring
pulls the satellite now this way, now that, thus altering its nodes, that
is, the points where the plane of its orbit crosses the planet's equator,
and also its apsides, or the points in which the satellite's orbit is
nearest and farthest front the planet. The effect of an equatorial
protuberance tilted thus is to shift these points round the orbit, the line
of nodes retrograding, while contrarily the line of apsides advances. From
the speed with which these revolutions take place, it is possible to
calculate the size of the bulge. Hermann Struve has just done this for the
lines of apsides of the two satellites of Mars, and finds for the value for
the consequent polar flattening of the planet 1/190 of its equatorial
diameter. From these two independent determinations we may conclude that the
value found at Flagstaff is pretty nearly correct.
We find, then, that Mars is a little flatter than our Earth, though not
noticeably so, the polar flattening amounting to about 22 miles.
The value, 1/190, for his polar flattening, hints that at some past time
Mars was in a fluid--that is, a molten--condition, just as the Earth's polar
flattening of 1/303, similarly shows her to have been, and that in both
cases the flattening was then impressed. Now, inasmuch as the tides, lunar
and solar in the case of the Earth, solar practically alone in the case of
Mars, have been slowing up the planet's rotation ever since this
refrigeration happened, but as their respective rates of rotation still
agree substantially with what a fluid condition demands, it is evident that
in the case of neither planet could the cooling have begun so very long ago,
but that it began longer ago for Mars than for the Earth.
In so far, then, we trace a certain similarity of development in the early
chaotic stage of evolution of the two planets, a stage pre-natal to their
career as worlds.
From these basic facts of size and shape we will now go on to more
latter-day detail.
II. Orbit
To determine whether a planet be the abode of life in the least resembling
that with which we are acquainted, two questions about it must be answered
in turn: first, are its physical conditions such as render it, in our
general sense, habitable; and secondly, are there any signs of its actual
habitation? These problems must be attacked in their order, for unless we
can answer the first satisfactorily, it were largely futile to seek for
evidence of the second.
III. Size and Shape
With the telescope we enter upon a new phase in our knowledge of the planet:
the determination of its shape and size.
See Plates
15 16
16 17
17
 Huyghens' drawing of the Syrtis Major, Nov. 28, 1659 7 P. M.
Reproduced from Flammarion's "La Planete Mars."
Huyghens' drawing of the Syrtis Major, Nov. 28, 1659 7 P. M.
Reproduced from Flammarion's "La Planete Mars."
Go to next chapter

WebGlimpse
Search:
The neighborhood of this page
The full archive
Go to line