A simple method to find the angular velocity of an asteroid

In the "Astrometry of Asteroids" exercise, some students may become bogged down in the conversion calculations, changing Right Ascension from Hours, Minutes, Seconds into decimal degrees and then arcseconds. If you wish, you may tell your students to derive the angular velocity of the asteroid in a simpler manner.

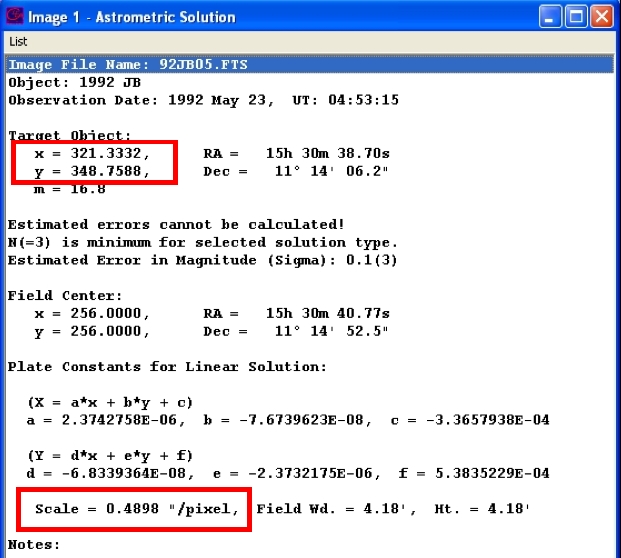
Look carefully at the Astrometric Solution from each image. It should look something like this:

Note the sections outlined in red. The asteroid's position is given in PIXEL coordinates, and the conversion between pixels and arcseconds (sometimes called the "plate scale") is also provided.

If we look at the solution to a second image, we again see the position of the asteroid in pixel coordinates:

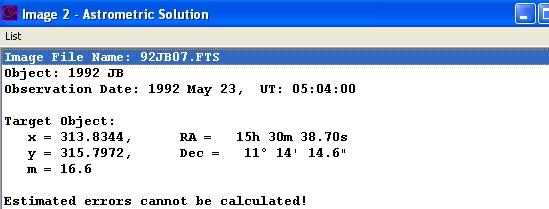
We can now compute the displacement of the asteroid in PIXEL coordinates very simply:

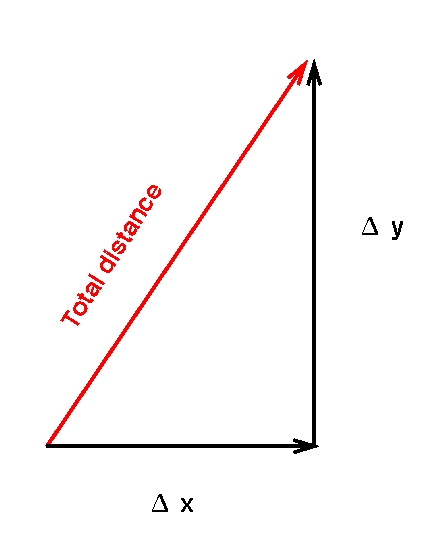
   Delta X   =   313.8  -  321.3   =   -7.5  

   Delta Y   =   315.8  -  348.8   =  -28.0  


   total distance  =  sqrt [  (-7.5)*(-7.5)  + (-28.0)*(-28.0)  ]

                   =  sqrt [        840.25      ]   

                   =    29.0    pixels

Now, the plate scale portion of the astrometric solution tells us that each pixel is equivalent to 0.4898 arcseconds. Therefore,

                                                    arcseconds
   total distance  =   ( 29.0 pixels ) *  ( 0.4898 ------------ )
                                                      pixel

                   =    14.2  arcseconds

And ... we're done.