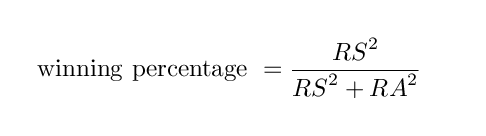
Bill James found a relatively simple relationship between the number of runs a team scores (RS) and allows (RA), and that team's winning percentage:
The exact value of the exponent -- shown as "2" in the classic formulation -- is a matter of some debate (see the article by Davenport and Woolner for one example). There is no doubt, however, that the relationship does a pretty good job of predicting the actual winning percentage of real baseball teams. For example, consider teams in the major leagues' 2006 season.
# Team RS RA actual predict error in # wins wins prediction # ---------------------------------------------------------- NY_Yankees 930 767 97 96 1 Toronto 809 754 87 87 0 Boston 820 825 86 81 5 Baltimore 768 899 70 68 2 Tampa_Bay 689 856 61 64 -3 Minnesota 801 683 96 94 2 Detroit 822 675 95 97 -2 Chicago_Sox 868 794 90 88 2 Cleveland 870 782 78 90 -12 Kansas_City 757 971 62 61 1 Oakland 771 727 93 86 7 LA_Angels 766 732 89 85 4 Texas 835 784 80 86 -6 Seattle 756 792 78 77 1 NY_Mets 834 731 97 92 5 Philadelphia 865 812 85 86 -1 Atlanta 849 805 79 85 -6 Florida 758 772 78 80 -2 Washington 746 872 71 68 3 St._Louis 781 762 83 83 0 Houston 735 719 82 83 -1 Cincinnati 749 801 80 76 4 Milwaukee 730 833 75 70 5 Pittsburgh 691 794 67 70 -3 Chicago_Cubs 713 834 66 68 -2 LA_Dodgers 820 751 88 88 0 San_Diego 731 679 88 87 1 San_Francisco 746 790 76 76 0 Colorado 813 812 76 81 -5 Arizona 773 788 76 79 -3
Perhaps a graph shows the success of the formula more clearly.
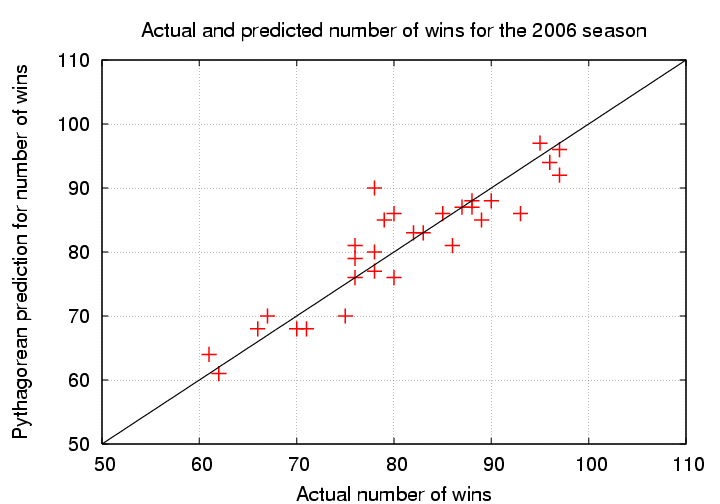
So, the formula does work. My question is -- should it work? That is, should there be any such simple relationship between runs scored, runs allowed, and winning percentage? More specifically, is such a formula a general rule, to be expected in all situations, or does it happen to hold only in a narrow set of circumstances (which, obviously, must include the real baseball world)?
There are many ways one might address this question. Some might involve very detailed calculations or play-by-play simulations of baseball games. I'm going to try a much simpler idea: generate only the final scores of a number of baseball games between two teams, according to a particular recipe, and then compare the actual won-loss record of each team to the Pythagorean prediction. The question is -- what recipe to use? We require
As a first attempt, let's try the Poisson distribution. It's a mathematical algorithm for predicting the number of discrete events (such as runs scored in a game) which will occur during some period, given the average rate of the events. It is also provided in many libraries of mathematical routines, so it's easy to find.
Is it really a good match the actual distribution of runs scored by real baseball teams? I happen to have the game scores for two seasons of the Boston Red Sox; let's see how well the real numbers compare to the Poisson distribution. The parameter λ for the Poisson function should be the average number of runs scored by a team per game, so
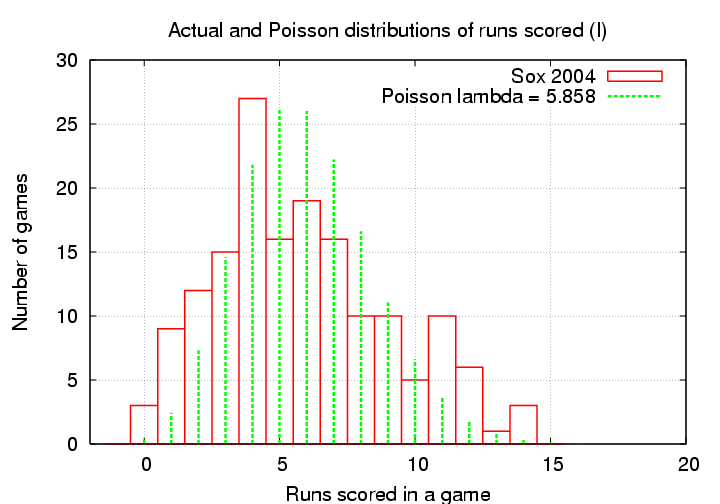
Hmmm. That's not a bad fit, but not a great one. The Poisson distribution fails at both ends: it predicts too few shutouts and too few blowouts.
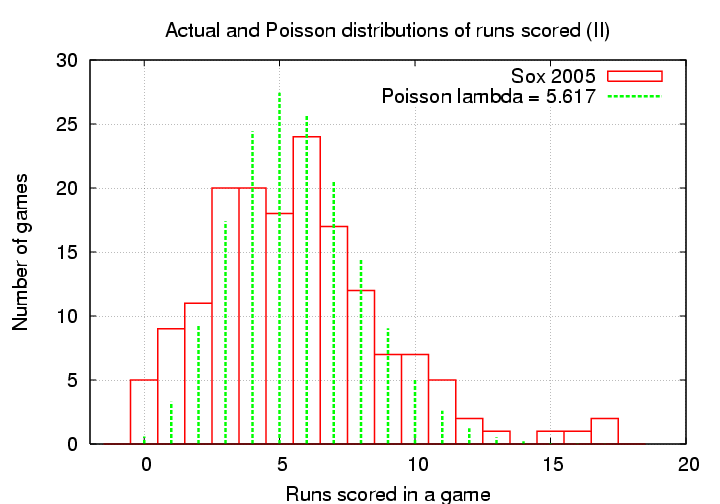
Once again, we see that the Poisson distribution is more sharply peaked than the real distribution.
Sigh.
The Poisson distribution isn't a great match, but let's go ahead and use it. I'll look for a better model a bit later ...
We'll start with a simple example: team A scores 6.0 runs per game (RPG) and team B scores 5.0 runs per game. Each team's scores are drawn from a Poisson distribution. The teams play a season of 162 games against each other. How many games does A win?
The Pythagorean theorem (with power 2.0) predicts that team A should win a fraction
(6.0)2
--------------------- = 0.590
(6.0)2 + (5.0)2
of the time; that adds up to 95.6 wins.
I wrote a little program to draw random values from
Poisson distributions (using routines from the
Gnu Scientific Library )
and simulate many seasons of this head-to-head matchup.
The simulations yield an average number of wins for team A
of 102 games, with a standard deviation from the mean of 6 games.
Thus, in the simulations, the high-scoring team wins more
games than predicted by the basic Pythagorean formula;
the difference between prediction and simulation is a bit
larger than the standard deviation in the simulations, too.
Hmmmm.
Suppose we try a different exponent: 1.8. Then the prediction is
(6.0)1.8
------------------------ = 0.581
(6.0)1.8 + (5.0)1.8
This is only slightly different, predicting 94.2 wins instead of 95.6. Note that this takes us even farther away from the simulation's average of 102 wins.
Do the simulations consistently differ from the Pythagorean predictions? Let's go back to the simple version of the Pythagorean formula with exponent p = 2.0. Suppose we look at a series of teams which always differ by exactly one run per game:
team A RPG team B RPG Pythag A wins sim A wins
----------------------------------------------------------------
4.0 3.0 103.7 108.6
4.5 3.5 100.9 106.1
5.0 4.0 98.8 105.2
5.5 4.5 97.0 104.0
6.0 5.0 95.6 102.5
6.5 5.5 94.4 101.7
----------------------------------------------------------------
When we consider a large number of situations, it helps to make a picture of the results. This graph shows the results of the simulations described in the table above. The number of wins predicted by the Pythagorean formula are a little bit different in the graph, because they are based on the actual number of runs scored per game in the simulation; the random number generator didn't always produce exactly 4.0 runs per game for one team over the course of 162 games, so I took the actual number of runs scored by each team for each simulated season and plugged into the formula.
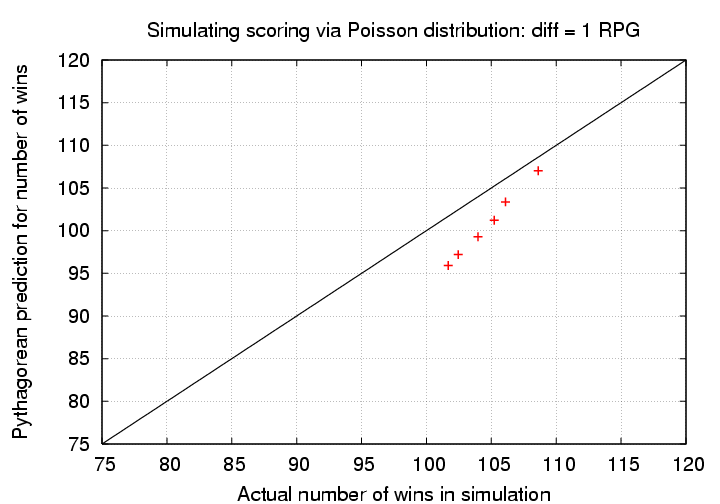
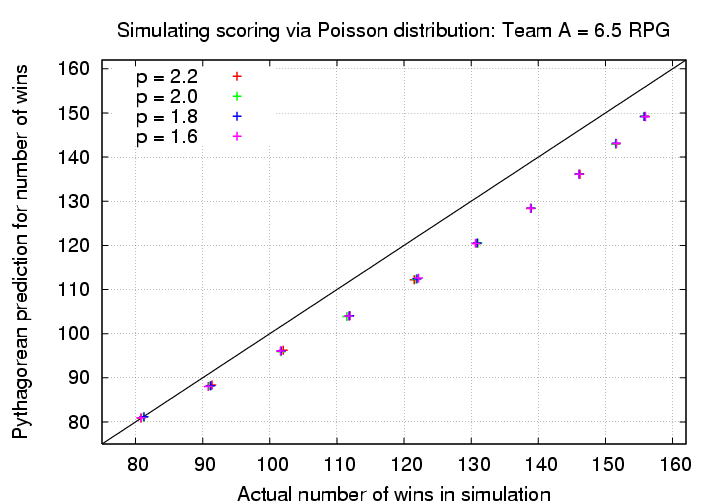
The Pythagorean formula (with exponent p = 2.0) always underpredicts the performance in the simulations of the high-scoring team; the difference appears to shrink as the winning percentage increases. In other words, the Pythagorean formula appears to do best when the typical scores are low, and, for a fixed difference of 1 RPG, the high-scoring team wins much more frequently than it loses.
Now, let's see if choosing a different exponent causes the formula to agree any better with the simulations.

Nope. No matter which exponent we choose, we find the same result: the Pythagorean formula underpredicts the number of wins by the higher-scoring team; for a fixed difference of 1 RPG, the formula does better when both teams score relatively few runs.
Let's slice the data in a different manner: suppose we focus one a team which has a fixed scoring rate -- say, 6.5 RPG. We'll vary the number of runs scored by the opposing team, from 2.0 RPG in steps of 0.5 RPG, until the opposing team reaches the same rate of 6.5 RPG. Again, we'll use the simple exponent p = 2.0 in the Pythagorean formula to start.
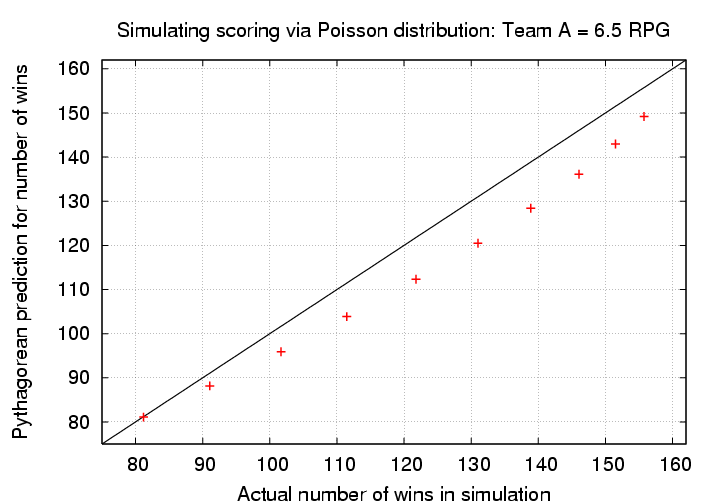
In this case, the formula matches the simulations well when both teams score at roughly the same rate; but when one team scores significantly more runs, the formula (as before) underpredicts the success of the high-scoring team.
Different choices for the exponent make no material difference in this discrepancy.