Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
This document is intended to give a brief, simplified view of the forces which act on a baseball as it makes its way from the pitcher's hand to home plate, meets the bat, and then flies back out toward the fences.
To begin, let's remove all the air from a baseball stadium (and hope that the players have pressure suits). In a vacuum, there will be only one force acting on the baseball after it leaves the pitcher's hand: gravity.
Q: What is the size and direction
of the gravitational force on a baseball?
The size of the force is just m*g, the mass of baseball times the acceleration due to gravity; for a standard baseball, that is 1.4 Newtons. The direction, of course, is straight down.
Let's consider a relatively standard pitch: a fastball thrown at 90 miles per hour (mph); to be precise, thrown so that it is travelling at 90 mph as it leaves the pitcher's hand. The center of the strike zone should be over the middle of the plate and about 33 inches or 2.77 feet above the ground (it depends on the height of the batter, of course). Here's the trajectory of a fastball which ends up in the center of the strike zone, as seen from the third-base side of the field.
You can count the dots above to see that the ball arrives at the plate about 0.41 seconds after it leaves the pitcher's hand.
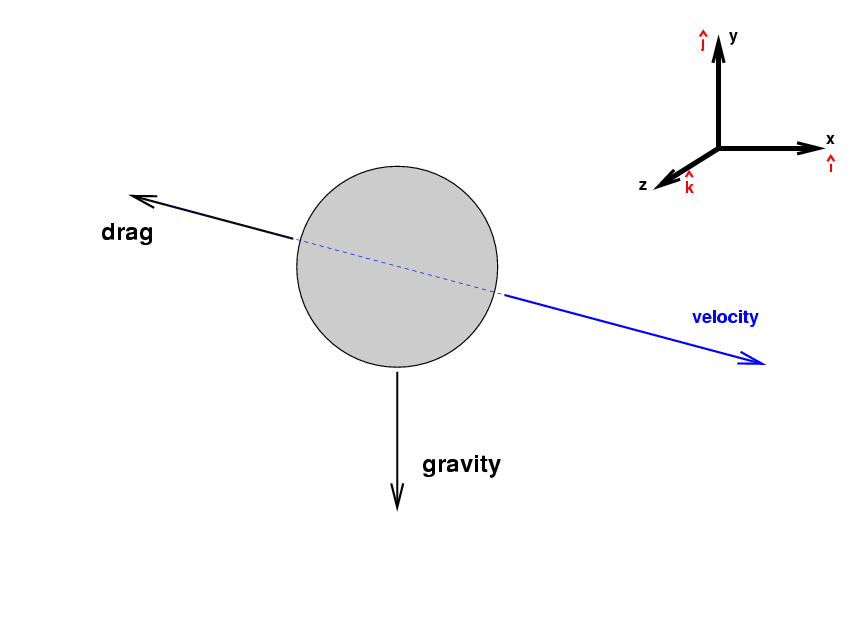
Of course, in real life, balls will slow down as they move through the air. As the ball moves through the air, it has to push the air out of its way. The air, in return, pushes the ball back, in the opposite direction. Therefore, the direction of the drag force will always point opposite to the instantaneous velocity.
The size of the drag force is a bit complicated: it depends on the ball's speed. For the relatively narrow range of speeds of interest for pitching -- say, 60 mph to 100 mph -- the drag force is roughly dependent on the SQUARE of the ball's speed. We can write this approximation as
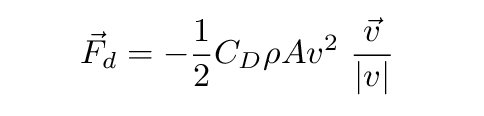
CD = drag coefficient = 0.40
ρ = density of air = 1.23 kg/m3
A = cross section area of ball = 0.00426 m2
v = velocity of ball (m/s)
For a pitch travelling at 90 mph towards home plate, the force of air resistance pushes it (mostly) backwards, toward the mound. The size of this drag force is about 1.7 Newtons.
Q: Which is larger in size, the drag
force or the gravitational force?
The figure below compares the paths of a fastball thrown with identical speeds and directions, one in a vacuum, the other through air:
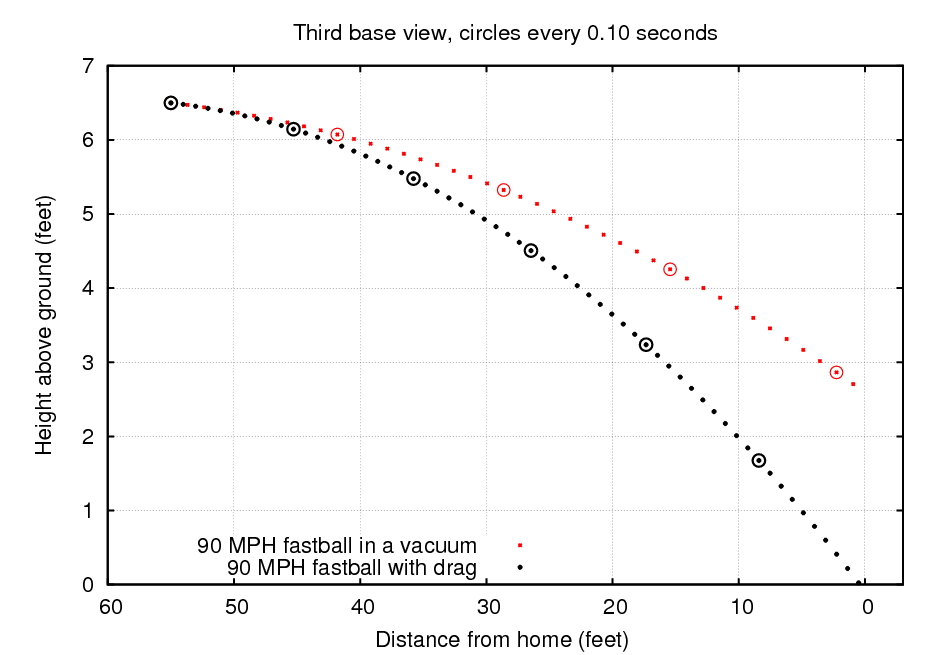
There are two main differences due to the drag force:
By the time it reaches the plate, the fastball in air isn't moving 90 mph any more. Its horizontal speed is about 80 mph, so a 90 mph fastball loses about 10 mph due to air resistance by the time it reaches the batter. This loss of speed is larger for pitches which start out faster -- after all, the drag force does grow with the square of the speed.
initial horizontal speed final horizontal speed loss ---------------------------------------------------------------------- 100 mph 88 mph 12 mph 90 mph 80 mph 10 mph 80 mph 71 mph 9 mph 67 mph 59 mph 8 mph ----------------------------------------------------------------------
A spinning object moving through the air will experience an additional force, due to the the interaction of its surface and the air: one portion of it will be rotating WITH the air, while another portion will be rotating AGAINST the air. There are several ways to characterize this interaction, and the resulting force. For our purposes, I'll refer to it as the Magnus force, and adopt a relatively simple equation to quantify its effect:
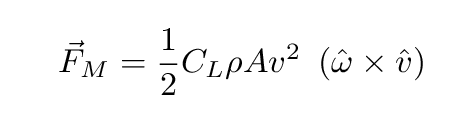
where
CL = lift coefficient (see below)
ρ = density of air = 1.23 kg/m3
A = cross section area of ball = 0.00426 m2
v = velocity of ball (m/s)
Let's wait for a moment to discuss the
lift coefficient CL,
and ask instead, "In which direction does the
Magnus force push the baseball?"
The last section of the equation above provides the
answer, if you know how to read vector notation:
means that
the direction of the Magnus force is
perpendicular to both
the ball's axis of rotation
and the ball's velocity
.
It will be easier to understand with a picture, which like all the others so far is taken from the third-base dugout, looking towards the pitcher's mound. I'll give the ball pure backspin, so that the rotation axis is horizontal.
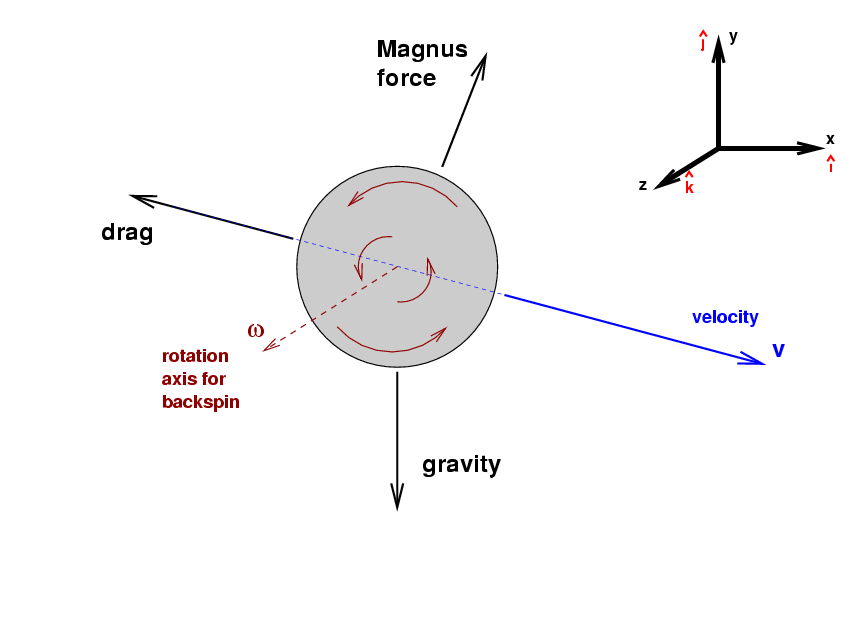
With pure backspin, the rotation axis must be horizontal ... but
should the direction of
point towards first base, or towards third base?
The rule is that, if you hold your right hand on the axis
and wrap your fingers around it in the direction of rotation,
your outstretched thumb points in the direction of the
vector describing the rotation.
In this case, if we wrap the fingers of a right hand
around the ball in the figure above to match the ball's rotation,
that right hand's thumb will point towards third base.
Phew.
Once we have the directions of
and
,
we can use the standard mathematical cross product
to determine the direction of the Magnus force.
Perhaps you'd like to read a brief review of the vector cross product?The rule again involves one's right hand: point your outstretched fingers so that they point along the direction of the first vector,
,
then orient your hand so that when you curl your fingers
to make a fist, the finger move towards the second vector,
.
Now stretch your thumb outwards, and it will point in the
direction of the cross product.
In this case,
that turns out to be mostly upwards.
Let me repeat that: when a pitcher throws a ball with pure backspin, the ball is pushed upwards as it moves through the air.
How large is this Magnus force? That depends on the speed of the pitch, and the rate at which the ball is spinning, but for rough purposes, we can use an approximate value of about 0.9 Newtons. Notice how all three forces are comparable in size:
gravitational force: 1.4 Newtons down
air drag force: 1.7 Newtons backward
Magnus force: 0.9 Newtons depends on spin
When throwing a fastball, the pitcher lets the ball roll off his fingers; as it rolls, it picks up backspin. The Magnus force due to backspin pushes the ball up, so a real fastball's trajectory lies ABOVE the trajectory of a pitch which has no spin.
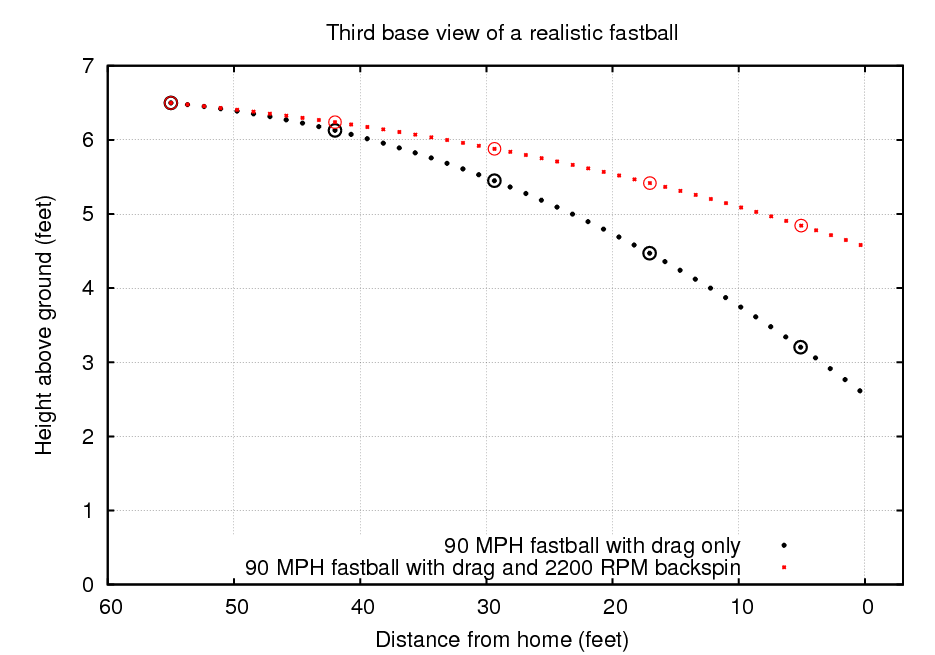
Holy mackerel! The backspin on a real fastball has a MAJOR effect on its trajectory. The spinning ball ends up about 2 feet higher than the "dead" ball when it crosses home plate.
Of course, if one were throwing a ball with the same size as a baseball but less mass, then
In that case, one might be able to throw a ball so that it rises quite a bit on its way to the plate. You can click on the picture below to see some examples from a Wiffle Ball tournament; I suggest starting at 2:14 from the beginning of the clip.
Yes, yes, a whiffle ball has holes on just one side, which causes all sorts of extra aerodynamic effects.
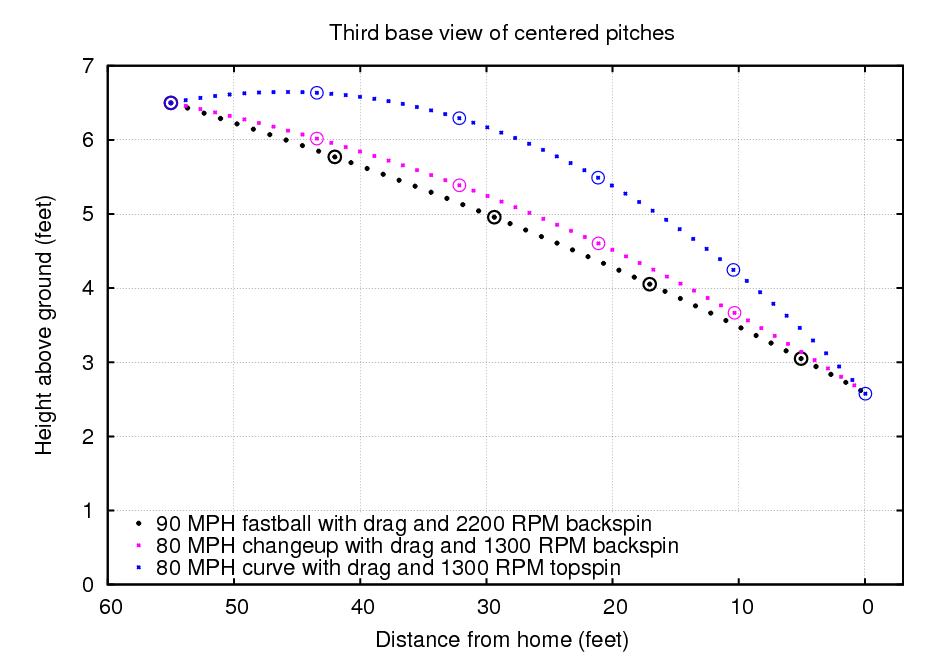
Finally, let's consider a simple curveball, thrown with pure topspin. Most real curveballs have a considerable amount of sidespin as well, but let's leave that complication for later. Topspin means that the axis of rotation points towards the first-base side of the field.
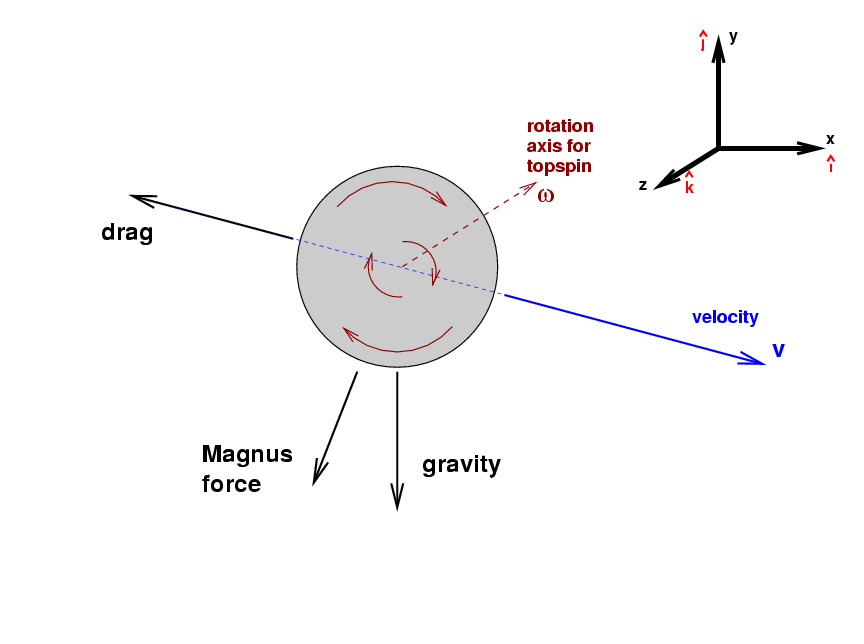
If we perform the cross product of
and
now,
we'll find that the result points mostly downwards.
With two forces pushing them downwards,
curveballs drop very rapidly.
In fact, if one throws a curveball with
exactly the same initial direction as a fastball,
it won't even reach the plate!
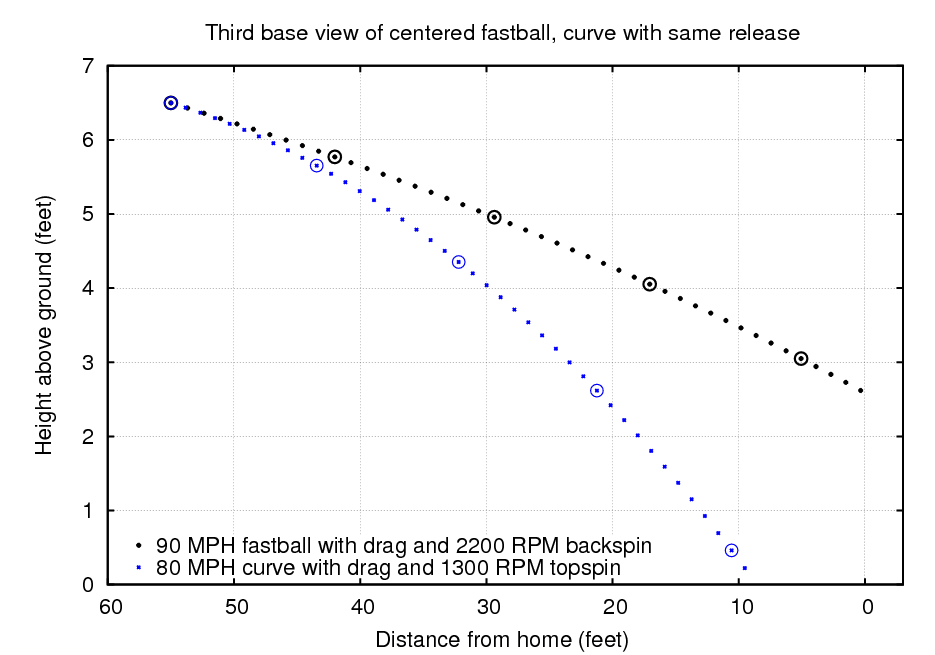
If you want a curveball to end up in the middle of the strike zone, you need to give it an initial velocity which is slightly ABOVE the horizontal:
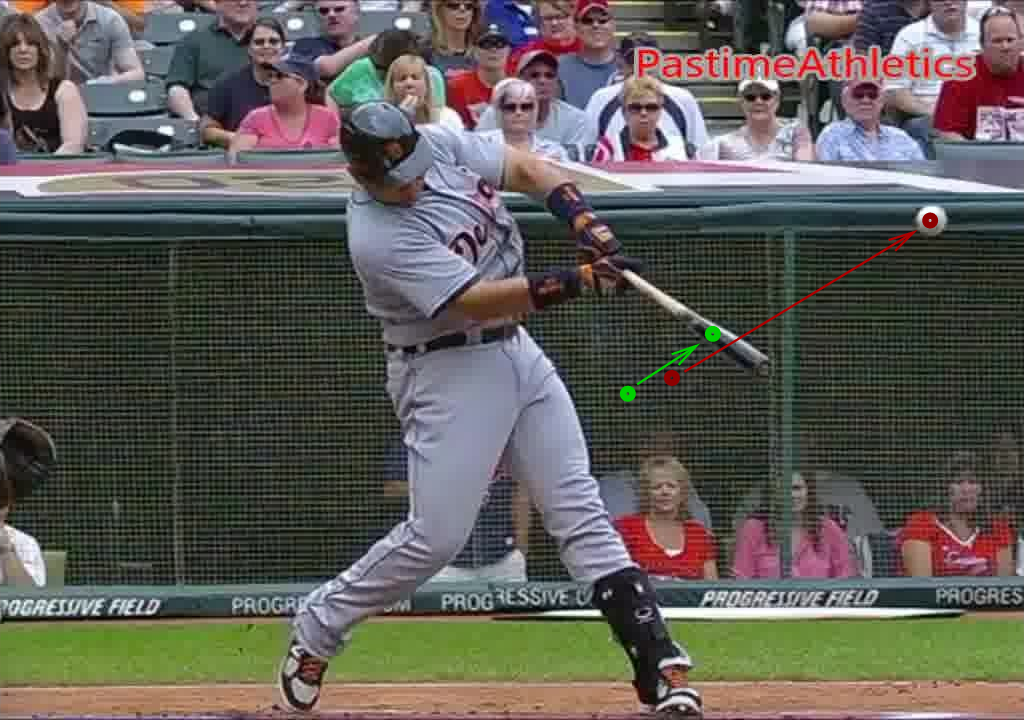
To illustrate the nature of a collision between ball and bat, let's watch this super-slow-motion clip of Detroit Tigers first baseman Miguel Cabrera (click on image to animate):
Video courtesy of
PastimeAthletics
What's going on here? Well, before they meet, the ball is flying toward home plate, while the bat is moving out toward the mound.
Q: Which is moving faster?
Let's find out.
Aha. We can see that the ball is moving slightly faster than the bat. If we assume that the pitch is a standard 90 mph fastball, then the bat must be moving at about 73 mph.
Now, after the collision takes place, the ball reverses course and flies off toward the fences at high speed, while the bat continues to plow forward ...
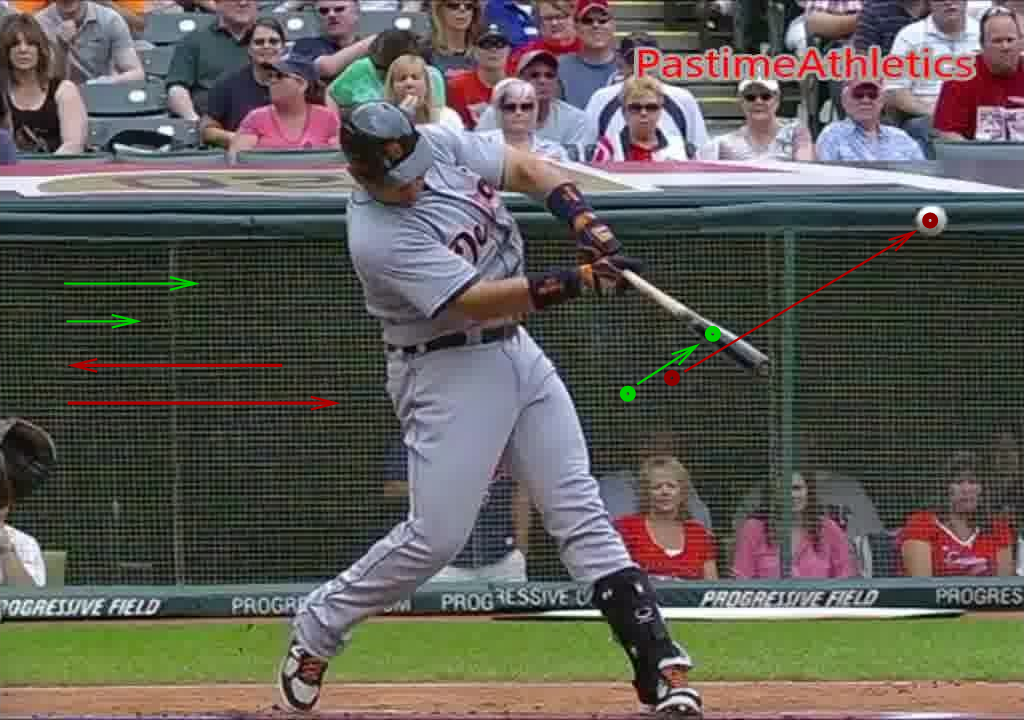
If we compare the speeds of each object before and after the collision, we can see that the ball ends up gaining speed, but the bat moves more slowly afterward.
Now, if we use a little physics, and a little mathematics, we can come up with an equation which will allow us to compute the final speeds of the ball and the bat in a quantitative manner.
One key to understanding this collision is the concept of momentum, which is combination of the mass and velocity of each object. It turns out that momentum is conserved in collisions, which means that
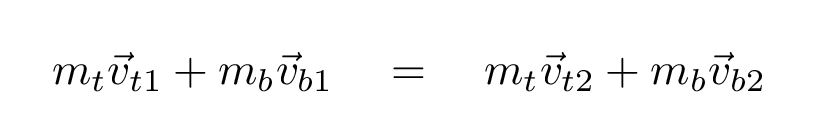
We can use a second connection between the initial and final speeds, based on the idea that the final speed of the ball relative to the bat is just a fraction e of its initial speed relative to the bat. That fraction e, called the coefficient of restitition, depends in a complicated manner on the structure of the ball and bat; I'll just assume it has a constant value of e = 0.4
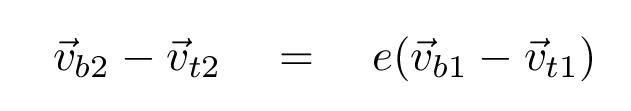
With these (simplified) assumptions, we can compute the final speed of the ball as long as we know the initial speeds of the ball and the bat, and their masses.
Now, a batter can't choose the speed of an incoming pitch, but he can decide what sort of bat to swing.
Q: What sort of bat should the hitter choose?
Well, if they are moving at the same speed, a massive bat will project the ball much faster than a lightweight bat:
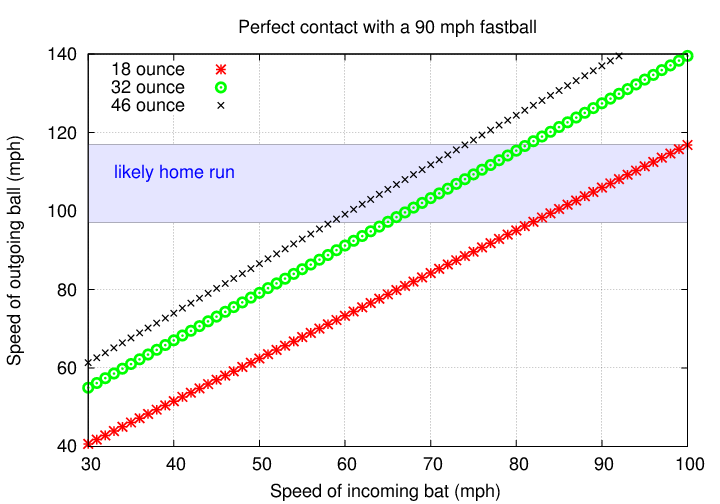
The trouble, of course, is that it's hard to swing a heavy bat!
In order to accelerate the bat around in an arc to meet the ball over the plate, a batter must apply a torque with his legs, hips, torso and arms.
What's torque? A twisting force, basically.
You may recall the connection between the linear force applied to an object, its mass, and its linear acceleration -- remember this?
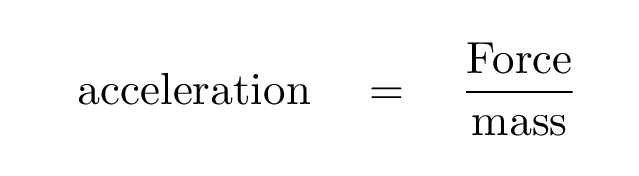
There's a similar relationship between the torque applied to an object, its moment of inertia, and its angular acceleration.
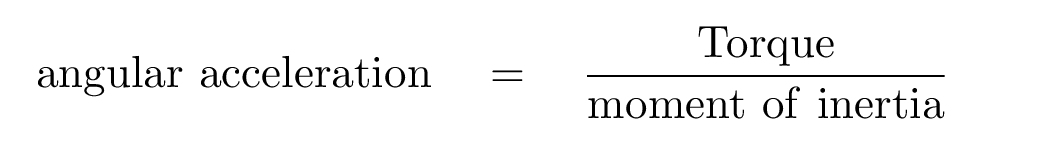
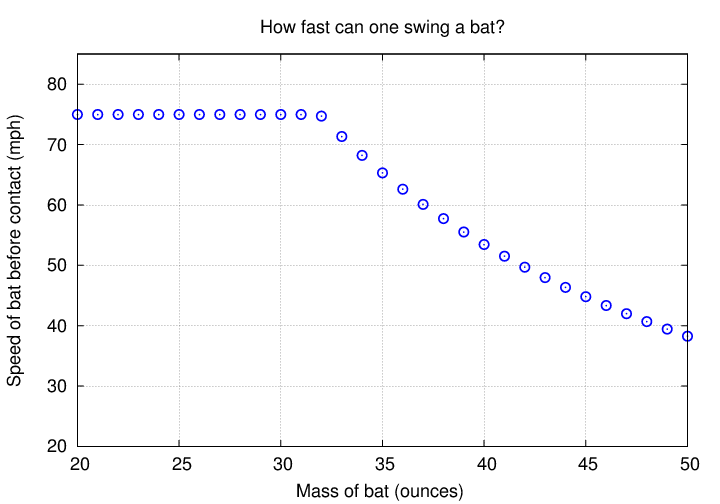
The big problem here is that the moment of inertia of baseball bat -- its resistance to being swung around in a circle -- increases very rapidly with its mass. Switching from a 30-ounch bat to a 31-ounce bat of the same shape, an increase of just 3 percent in weight, increases its moment of inertia by about 10 percent!
Even major-league players can't swing heavy bats as fast as light ones. A simple model of the swinging motion predicts that bat speed will fall rapidly as the weight increases:
If we combine this effect of a bat's weight on the speed of its swing with the physics of the collision, we can see that there must be a small range of bat weights which will produce the best results.
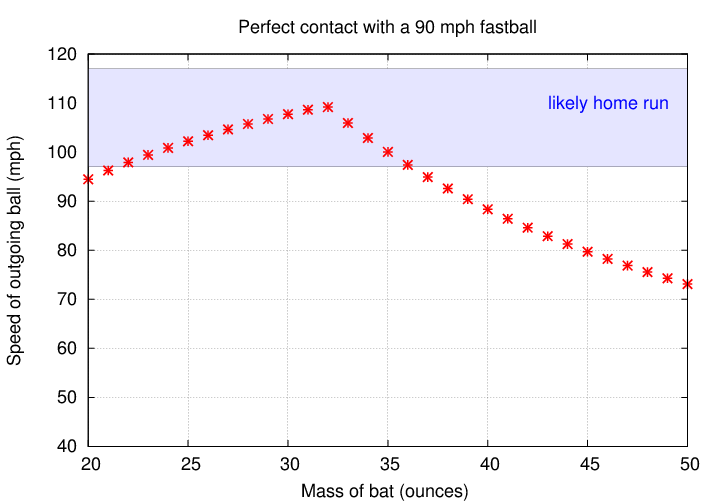
This "ideal bat weight" will shift a bit to lighter or heavier values, depending on the maximum torque that a batter can exert.
What happens after the batter strikes the ball? The ball flies up into the air and travels toward the outfield. Will it make it over the fence for a home run, or be caught by an outfielder? The answer depends on three factors:
Just as we applied the laws of physics to compute the motion of a pitch, we can use them to determine the trajectory of a batted ball. Let's start with a simple (and unrealistic) case, and work our way up to the real thing. We'll adopt an initial speed of 105 mph, which is near the top end for major league batters.
If there were no air resistance, and no Magnus force, then the only influence on a ball would be gravity. In that case, its motion would be relatively simple.
Q: If the ball were travelling in a vacuum,
what initial angle would cause it to go
the maximum possible distance?
Q: Can you guess how far a ball at 105 mph
and that optimal angle would travel,
if there were no air?
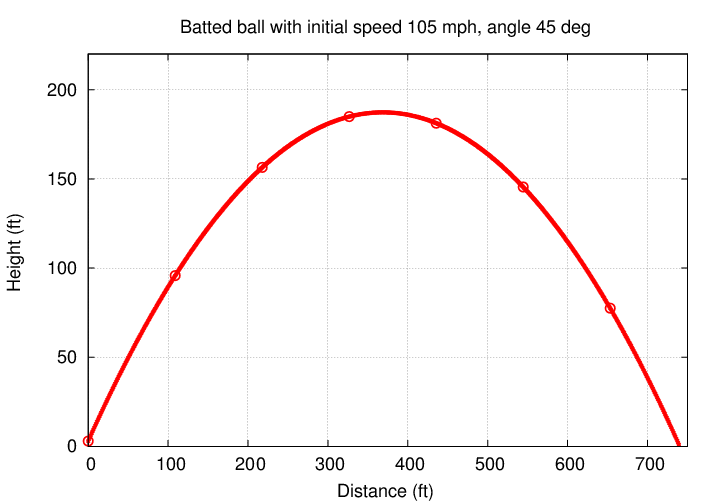
Holy Cow! In the absence of air resistance, batters could send Mr. Spaulding on some pretty long journeys!
But, of course, humans do play ball on the surface of the Earth, where the drag force due to air slows balls considerably.
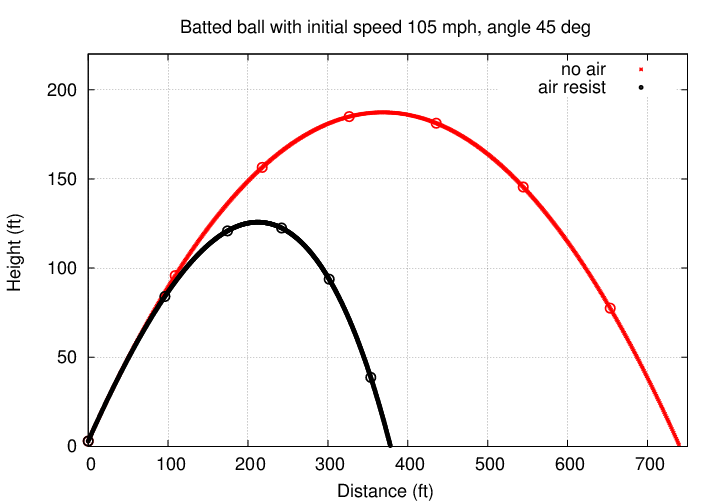
Our 105-mph ball doesn't even make it to the warning track. Ugh.
Could we increase its distance by giving it a different initial angle?
Q: Should we try angles
LESS than 45 degrees above horizontal
or
MORE than 45 degrees above horizontal?
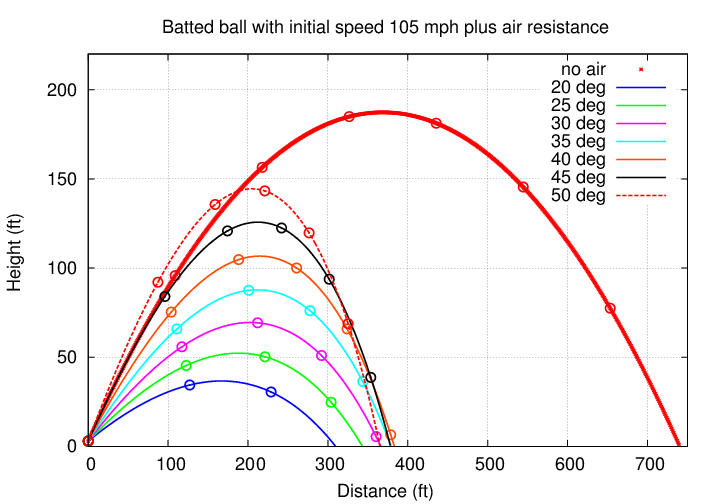
When the ball encounters air resistance, it will go farther if its initial angle is less than 45 degrees. In this particular example, the best choice is about 40 degrees ... but that still leads to a fly ball out.
So, how are real players able to hit home runs? Well, the one factor we haven't included yet is the Magnus force. If the ball leaves the bat with a strong backspin, then the Magnus force will push the ball up, acting against the force of gravity, and allowing it to stay in the air for an extra second or more. With all that extra time, the ball can travel farther toward (and over) the fence.
In the calculations below, I gave the ball backspin at a rate of 1500 RPM.
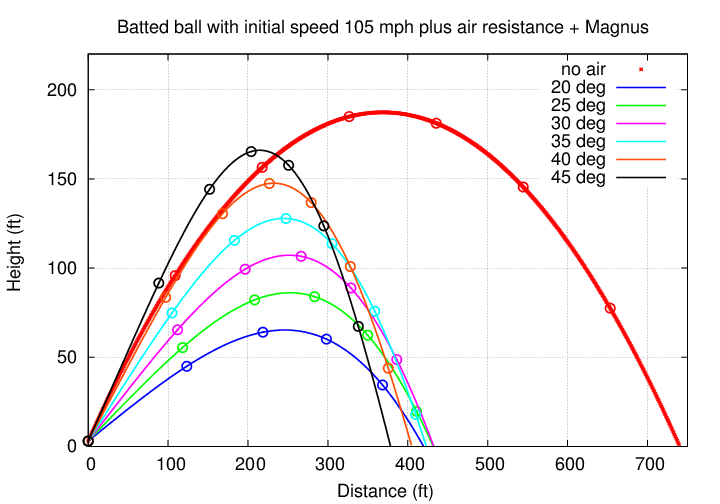
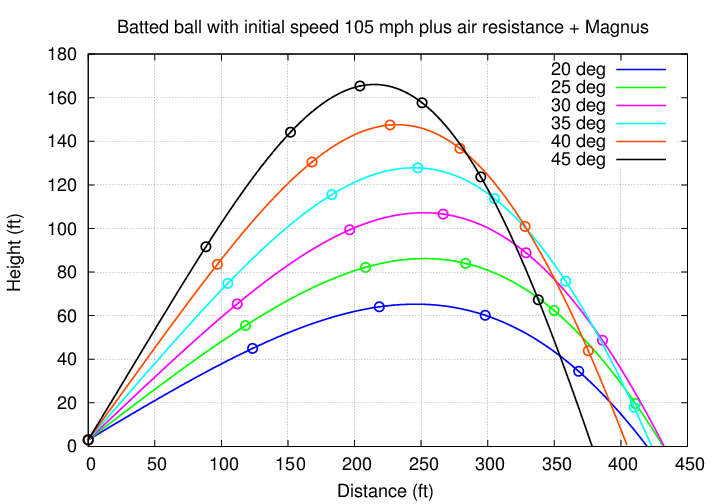
When we include all the real effects -- air resistance and the Magnus force -- then we see that a ball struck at 105 mph, with plenty of backspin, at a relatively low angle (25 - 30 degrees), can reach a distance of 420 feet or more from home plate. That's far enough to be a home run in most ballparks.
Of course, some batters can do even better than that. The Statcast Leaderboard website provides detailed information on the properties of batted balls from many MLB games. A rookie for the Yankees named Aaron Judge, in a game on June 11, 2017, absolutely crushed a pitch from the Orioles' Logan Verrett:
Data courtesy of
Statcast Leaderboard
(click on the image below to activate a video of the home run)
If you enjoy thinking about baseballs and how far they might fly, consider downloading the Trajectory Calculator, an Excel spreadsheet that can help you compute your own home-run distances.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.