Revised to use Contextual Runs to predict a team's performance, rather than OPS. You can still read the original version using OPS if you wish.
This question was posed as part of a discussion on the Sons of Sam Horn website . Eric Van asked the question:
What we want to know is whether there's a correlation between standard deviation of the principal hitters, and two things: Actual Runs - Calculated Runs according to EqA, CR, RC or other formula Actual Wins - Pyth Wins IOW, do consistent lineups score more or less runs than expected? Given however many runs they score, do consistent lineups win more or less games than expected?
I will attempt to address the first question: does the actual number of runs scored by a team depend significantly on whether the hitters are relatively uniform in quality, or vary greatly from batter to batter?
For the impatient among you, my conclusion is "No."
The basic data comes from baseball-reference.com's website . I used their list of the "main starting batters" for all American League teams during the period 1997-2006. For example, the 2006 Red Sox are listed like so:
Pos Player Ag G AB R H 2B 3B HR RBI BB SO BA OBP SLG SB CS GDP HBP SH SF IBB OPS+ ---+-------------------+--+----+----+----+----+---+--+---+----+---+----+-----+-----+-----+---+---+---+---+---+---+---+----+ C #Jason Varitek 34 103 365 46 87 19 2 12 55 46 87 .238 .325 .400 1 2 10 2 1 2 7 85 1B Kevin Youkilis 27 147 569 100 159 42 2 13 72 91 120 .279 .381 .429 5 2 12 9 0 11 0 108 2B Mark Loretta 34 155 635 75 181 33 0 5 59 49 63 .285 .345 .361 4 1 16 12 2 5 1 82 3B Mike Lowell 32 153 573 79 163 47 1 20 80 47 61 .284 .339 .475 2 2 22 4 0 7 5 106 SS Alex Gonzalez 29 111 388 48 99 24 2 9 50 22 67 .255 .299 .397 1 0 6 5 7 7 1 77 LF Manny Ramirez 34 130 449 79 144 27 1 35 102 100 102 .321 .439 .619 0 1 13 1 0 8 16 168 CF #Coco Crisp 26 105 413 58 109 22 2 8 36 31 67 .264 .317 .385 22 4 5 1 7 0 1 80 RF *Trot Nixon 32 114 381 59 102 24 0 8 52 60 56 .268 .373 .394 0 2 10 7 0 5 1 98 DH *David Ortiz 30 151 558 115 160 29 2 54 137 119 117 .287 .413 .636 1 0 12 4 0 5 23 164 ---+-------------------+--+----+----+----+----+---+--+---+----+---+----+-----+-----+-----+---+---+---+---+---+---+---+----+
I also grabbed the overall team stats, using all players, for each team.
By the way, the most time-consuming portion of this work was dealing with the changing name of the Angels team: they went from the California Angels to the Anaheim Angels to the Los Angeles Angels during this brief span. Sigh.
I will use simple OPS, defined as the sum of On-base-Percentage (OBP) and Slugging Percentage (SLG), as a measure of the quality of a batter. If batters have similar OPS, I judge them to be similar; if their OPS values differ greatly, I judge the hitters to be significantly different in quality.
In order to predict the performance of a team, I'll use a slightly modified version of Contextual Runs (CR).
Since my sources didn't list LOB, I set it to zero; sorry! I also scaled the result of the calculation by a constant factor so that, on average over the period of the study, the prediction was equal to the actual number of runs; that happened when I multiplied the CR value by 2.03.
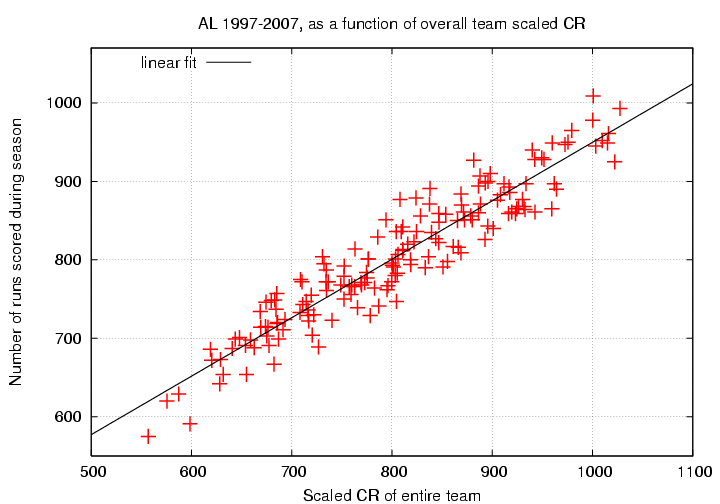
So, if we determine the linear relationship between my "scaled CR" value and the actual number of runs scored, we find:

The linear fit is
Runs = 204.6 + 0.745*(scaled CR)
scatter from fit = 28 runs
uncertainty in slope = +/- 0.040 runs/(scaled CR)
correlation coefficent r = 0.943
Those of you who read the earlier version will note that scaled CR does indeed predict actual runs scored better than OPS.
It's clear from the graph that some teams score more runs than this model predicts, and other score fewer. The question is -- are those differences from the basic model due to the inhomogeneity of the lineup? Suppose that they were; then we might expect lineups with a mixture of great and terrible hitters to score more runs (or fewer runs) than the model predicts. In that case, most of the points lying above (or below) the line would represent teams with a mixture of good and bad hitters.
One way to test this idea is to subtract from a team's ACTUAL number of runs scored the number of runs predicted based on its scaled CR. We can then plot this residual, in the sense
residual = (actual runs scored) - (linear model using scaled CR)as a function of the inhomogeneity of the main starting 9 batters. If the hypothesis is correct, we will see a correlation in the graph.
To quantify the inhomogeneity of the main 9 starters, I simply computed the standard deviation from their mean OPS during the season. In other words, using only the stats of the main 9 starting batters, I computed
sum ( OPS of each batter)
mean OPS = ---------------------------
9
2 2
( sum(OPS of each batter) - 9*(mean OPS) )
stdev OPS = sqrt( --------------------------------------------- )
( (9 - 1) )
For example, in the case of the 2006 Red Sox, the main 9 starters had a mean OPS = 0.814 and a standard deviation of 0.143. By comparison, the overall team OPS was 0.786, so the bench players were (as a group) rightly kept on the bench.
So -- do the residuals in runs scored over a season correlate with the inhomogeneity of the main 9 batters?
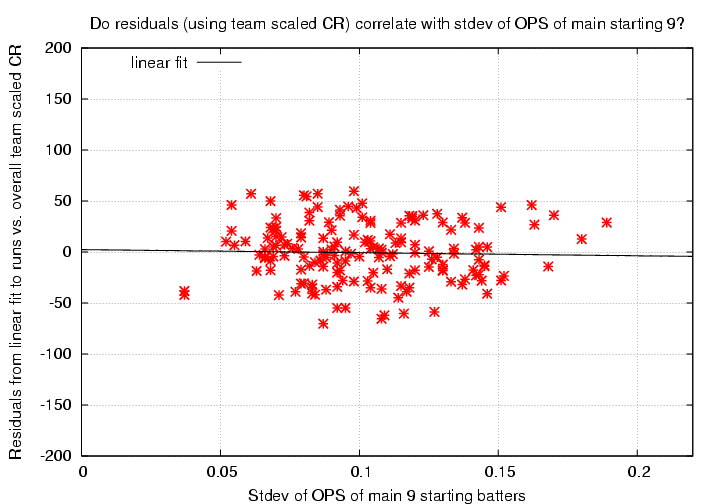
In a word, no: there is no correlation here. A formal unweighted linear fit to the residuals as a function of stdev of starting 9's OPS is
residuals = 2.334 - 23.711*(stdev OPS of starting 9)
scatter = 28 runs
uncertainty in slope = +/- 149 runs/(stdev OPS)
correlation coefficient r = -0.024
For the curious, I include here a few "top 10" and "bottom 10" lists generated during the course of this study. First, let's pick the teams which deviated most in a bad way -- underperformed, in other words -- from the linear model using scaled CR.
# # mean stdev mean residual #--------------------------------------------------------------------------------------------------- 1996 MIN starters ops 0.802 0.087 overall ops 0.778 runs 877 scaled cr 808.0 -70.3 2001 SEA starters ops 0.810 0.108 overall ops 0.805 runs 927 scaled cr 881.5 -65.5 1997 NYY starters ops 0.813 0.109 overall ops 0.798 runs 891 scaled cr 837.8 -62.1 2000 KCR starters ops 0.793 0.116 overall ops 0.773 runs 879 scaled cr 823.9 -60.4 1999 CLE starters ops 0.873 0.127 overall ops 0.839 runs 1009 scaled cr 1000.7 -58.7 1998 OAK starters ops 0.747 0.092 overall ops 0.731 runs 804 scaled cr 730.7 -54.9 2002 ANA starters ops 0.789 0.095 overall ops 0.774 runs 851 scaled cr 793.9 -54.8 2003 SEA starters ops 0.757 0.114 overall ops 0.754 runs 795 scaled cr 732.1 -44.8 1996 NYY starters ops 0.808 0.071 overall ops 0.796 runs 871 scaled cr 837.5 -42.3 2005 TOR starters ops 0.744 0.037 overall ops 0.738 runs 775 scaled cr 708.8 -42.2
I see no patterns here.
Let's look at the teams which overperformed the most relative to the prediction of their overall OPS:
# mean stdev mean residual #--------------------------------------------------------------------------------------------------- 2002 DET starters ops 0.691 0.096 overall ops 0.679 runs 575 overall cr 556.9 44.6 2000 TOR starters ops 0.832 0.162 overall ops 0.810 runs 861 overall cr 942.5 46.0 2002 BAL starters ops 0.717 0.054 overall ops 0.712 runs 667 overall cr 682.4 46.1 2003 CHW starters ops 0.796 0.101 overall ops 0.777 runs 791 overall cr 850.9 47.7 2005 CHW starters ops 0.768 0.068 overall ops 0.747 runs 741 overall cr 786.8 49.9 2005 TEX starters ops 0.815 0.081 overall ops 0.797 runs 865 overall cr 959.4 54.5 2005 BAL starters ops 0.784 0.080 overall ops 0.761 runs 729 overall cr 778.3 55.6 1999 DET starters ops 0.792 0.061 overall ops 0.761 runs 747 overall cr 804.5 57.1 2006 TBD starters ops 0.763 0.085 overall ops 0.734 runs 689 overall cr 726.8 57.2 2003 DET starters ops 0.711 0.098 overall ops 0.675 runs 591 overall cr 598.5 59.6
Hmmm. Detroit appears 3 times, Baltimore and the White Sox twice. This repetition might possibly suggest that there is some feature of these teams which causes them to do better than scaled CR would predict, but it could very well be chance.