
Executive summary: about 112 mph
In the July 26, 2011, issue of Wired magazine, Rhett Allain comments on the excellent throw Rich Ankiel made to throw out Willy Tavares at third base in a game played May 6, 2008. You can see a replay of the throw, and another one later in the game, by going to http://www.youtube.com/watch?v=ElNJzE04YhQ&feature=player_embedded#at=45 .
Allain provides the following information about this toss:
Using that information and some physics, he estimates that the ball left Ankiel's hand with a speed of 123 mph relative to the ground. That's pretty darn fast. I decided to see if I could reproduce this result, using some physics and some software I wrote a few years ago to analyze the motion of pitches.
The first step is to determine the two quantities of most interest, the distance of the throw and the time of its flight. I have access only to the YouTube copy of the replay, mentioned above, and will use it; analysis of some more original copy of the video would be better, of course.
For distance, I can make only a very rough guess. This camera was pretty close to the line running exactly down the center of the field; the horizontal position of second base is very nearly equal to that of the "415" marked on the fence in straightaway center. The camera may be a little bit to the left of this line, but it's hard to say.
Ankiel's position on the field must be to the left (third-base) side of the center when he releases the ball; just look at this picture, taken by the same camera:

However, his position in the plate-to-center direction -- that is, his distance from the fence, or from the infield -- is hard for me to estimate. My guess at his location when he releases the ball is shown below on a schematic of Coors Field which I found at http://www.andrewclem.com/Baseball/CoorsField.html.
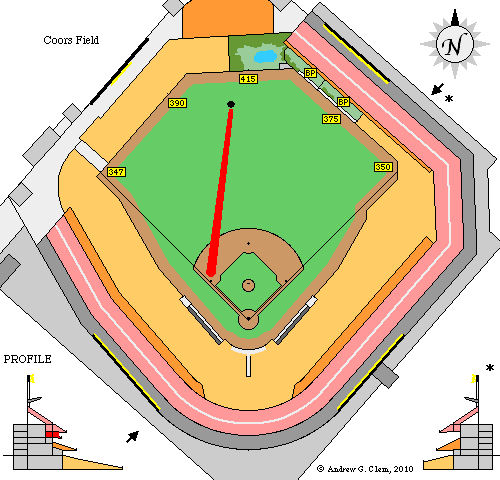
I used the schematic image to measure the distance of the throw in a simple fashion: I measured the distance, in image pixels, from home plate to the center-field fence, and then the distance from the black dot denoting Ankiel's position to third base. Assuming the first distance is 415 feet, I computed a distance of 300 feet for the throw. So, my distance of 300 feet = 91.4 meters is quite a bit shorter than the estimate of 101 +/- 3 meters made by Allain. I have no way to estimate the uncertainty in my distance, so I won't.
How long was the ball in the air? Allain estimates 2.84 +/- 0.03 seconds, referring -- I believe -- to the first throw, after the catch. Now, when I examined the video, I found that the camera cut away from Ankiel before he released the ball, in order to follow the runner going from second to third. I could see these events:
video frame 220 Ankiel's arm starts to come forward
as camera cuts away
video frame 300 ball enters third baseman's mitt
Fortunately, the camera does stay on Ankiel during his second throw, in the bottom of the eighth inning. I could watch his arm go back, come forward, and release the ball. Comparing the pictures of the start of the first throw to those of the second, it appears to me that about 5 video frames must have elapsed from the cut to the release. Thus, I estimate that the ball is in the air for 75 video frames.
How long is this in seconds? Well, that depends on the framerate of the original video. The "mplayer" program finds information in the header of the video which describes it as 59.75 frames per second, but when I watch it and compare the clock time to the count of frames, I get something around 25-30 frames per second. I am going to guess that the video is 30 frames per second, with the 59.75 referring perhaps to the number of "video fields" per secon (2 interlaced fields make up one video frame).
So, 75 video frames at 30 frames per second yields a time of 2.50 seconds in the air. This is considerably smaller than Allain's estimate of 2.84 +/- 0.03 seconds. However, his words
Using Tracker Video analysis, I get a much better estimate of about 2.84 +/- 0.03 seconds.
suggest that he may have used some rather sophisticated tools, which could very well be much more accurate than my estimates by eye; and he may know quite a bit more about the properties of this video than I do.
As Allain explains in his article, the situation is very simple if a ball travels through a vacuum. In that case, the only force acting on the ball is gravity, and the motion of the ball can be exactly described by a pair of simple equations.
If we know the starting and ending heights of the ball, and the distance and time it travels, we can figure out exactly how fast the ball must have been thrown. I made the following assumptions:
If gravity were the only force acting on the ball, we could use these equations to determine both the initial speed of the ball and its initial angle. In this case, we would find that a speed of 86 mph and an angle of 17.8 degrees above the horizontal would correspond to a time of 2.50 seconds. If we chose to adopt the time of 2.84 seconds instead, we'd find that the initial speed must have been 79 mph, at an angle of about 22 degrees.
Because the ball travels through the air, it is subject to two other forces, in addition to gravity.
You can read a lot more about these two forces in my document describing pitches. For now, let me describe very briefly how I'm computing these forces.
What is the net effect of these two forces? The graph below sums it up pretty clearly: it shows the trajectory of three baseballs, each of which is thrown with an initial speed of 90 mph and each of which travels horizontally a distance of 250 feet (yes, yes, Ankiel's throw was about 300 feet -- this graph simply illustrates the effect of air).
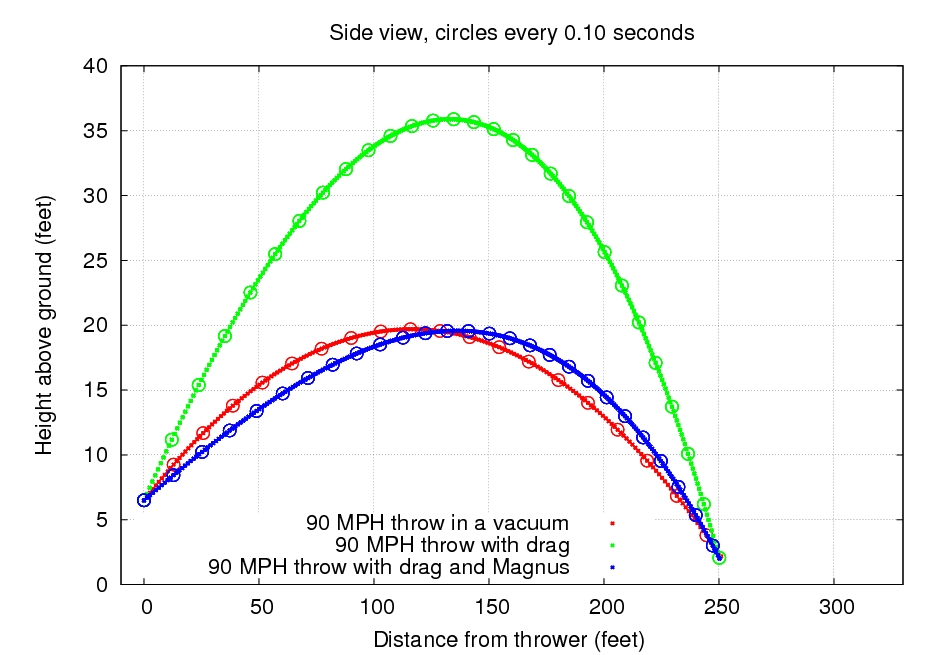
In the absence of air, the ball travels along a parabolic path (red line). If a drag force is present, it slows the ball down; so, if one threw a ball with the same trajectory as the red line, it would fall to the ground before reaching the target. In order to reach the target, one must throw the ball much higher -- along the green line. This high, arched green path takes much longer than the more direct red path.
The addition of the Magnus force changes things in a big way. For the most part, the Magnus force pushes the ball upwards, partially countering the force of gravity. As a result, the ball can be thrown with a low trajectory and still reach the target before it hits the ground; in fact, as the blue line shows, the trajectory of a ball with a good deal of backspin can be similar to the simple parabola of a ball thrown in a vacuum.
In short, a ball thrown through air with backspin can reach its target much more quickly than a ball thrown through air without any spin.
Using a bit of software I wrote which integrates the motion of a ball under the influence of all three forces, I computed the time required for a ball to travel from a initial height of 6 feet to a final height of 2 feet over a horizontal distance of 300 feet, with various combinations of initial speed and initial elevation angle. Let's look at the results.
Initial speed (mph) elevation angle (degrees) time (seconds) --------------------------------------------------------------------- 90 16.3 3.56 100 9.5 3.07 110 5.5 2.74 120 2.6 2.49 ----------------------------------------------------------------------
You can see how much lower the trajectory is for a high-speed throw in the graph below.
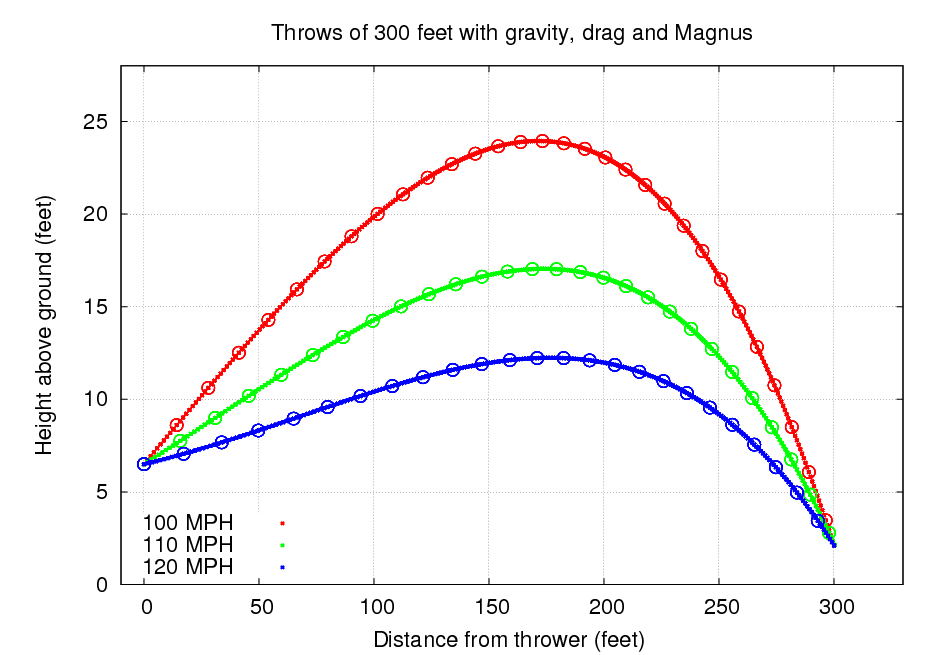
What does this mean for the initial speed of Ankiel's throw? Well, if my estimates for the distance (300 feet) and duration (2.50 seconds) are accurate, and if my assumptions about the drag and Magnus forces are correct (more on that in a moment), he must have released the ball with an initial speed of about 120 mph. That's pretty darn fast! Remember that this is the speed of the ball relative to the ground and the air, not relative to his hand or body. If you watch the video of his first throw, you can see that he is moving forward as he makes the throw; his body's motion is probably a bit faster than that of a pitcher. Still, that can account for only 5 mph or so of the overall speed.
If Allain's measurement of the duration of the throw (2.84 seconds) is correct, then the speed comes down a bit: I find that an initial speed of 107 mph and an initial elevation angle of 6.5 degrees will fit the data.
In fact, let's look at the sensitivity of the initial speed to small changes in several of the input quantities, to get a feeling for the precision of my result. This will also tell us which variables are the most important to measure precisely.
It appears that the initial speed is most sensitive to the assumed distance and the density of air.
I should adopt for the density of air a value of 1.066 kg/m^3, which is based on the altitude of Coors Field and on a temperature of 70 degrees Fahrenheit, which was the temperature recorded for the start of the game. Note that Ankiel's throw was in the bottom of the first, so the temperature probably hadn't changed much. Using that density of air, a distance of 300 feet and a duration of 2.5 seconds, I conclude that Ankiel threw the ball at a speed of about 112 mph.
I welcome feedback, corrections and suggestions from readers.