
Tomoe Gozen, painted by Hiroshige; image courtesy of The Museum of Fine Arts, Boston

Tomoe Gozen, painted by Hiroshige;
image courtesy of
The Museum of Fine Arts, Boston
Although there are many surveys of the night sky, it turns out that many of them are somewhat ill-suited to detecting brief flashes of light. What's the problem? Well, consider the following situation.
You go out at night and look to the North. There it is, a familiar asterism we all know and love.

Q: What asterism is this? Q: Of what constellation is this a portion?
So, you look up and enjoy the view for a time. Click on the image below to activate a movie showing the sky in half-second intervals.
Q: In what frame did the transient appear? Q: How bright was it?
Yes, for just half of one second, a brief flash of light appeared above the bowl of the Big Dipper:

In this example, I have inserted into the image a transient source of magnitude 2.0. That makes it just about as bright as the brightest of the Dipper's ordinary stars.
However, the light from the transient appears in just a single half-second image; after that, it disappears. When people take pictures of the sky, they usually choose exposure times which are considerably longer than 0.5 seconds.
Q: What will happen to the appearance
of the transient if I take a picture
with a 1-second exposure time?
Here's what it looks like in practice: a 1-second exposure.

Pretty much the same, isn't it? The transient is still clearly present, and it's one of the brightest sources. No big deal.
But if I take a picture with an exposure time of 5 seconds, things start to change perceptibly.

In this case, the flash appears for only one tenth of the exposure time; so, for 90% of the exposure, the transient contributes nothing, while photons are continuing to flood the camera from all the ordinary stars. It's no wonder that, by comparison, the transient appears to be somewhat fainter.
And if I take an exposure of 50 seconds, which is pretty typical for constellation pictures, the poor transient only contributes for 1 percent of the total time. As a result, it now appears as one of the faintest stars in the group:

The problem is that a long exposure will cause a brief flash of light to APPEAR fainter than it was during its brief appearance.

In fact, one can use the ratio of the duration of a flash to the exposure time of a picture to compute the apparent change in brightness of a transient source.
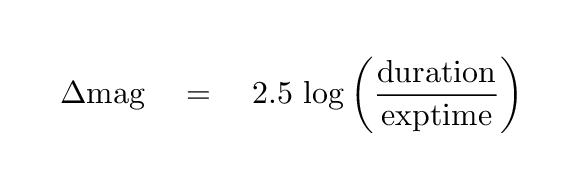
For example, suppose that a brief flash appears like a star of magnitude 5 during its 1-second duration. Then photographs of the following exposure times will show an object which appears to be somewhat fainter ...
Exptime Δ mag flash appears to be mag
------------------------------------------------------------------
1 0.0 5.0
2 0.8 5.8
5 1.7 6.7
10 2.5 7.5
30 3.7 8.7
60 4.4 9.4
600 6.9 11.9
3600 8.9 13.9
------------------------------------------------------------------
The solution to this problem is simple: just take short exposures! Unfortunately, that solution creates a few problems of its own ... among which is a veritable flood of data.
The camera is built around a special CMOS sensor built by Canon. It's a pretty big chip -- just compare it to a 5-yen coin:

What? You're not familiar with Japanese coins? Fine. Maybe this will give you a better idea of its size.

These chips allow one to read out very quickly while retaining a very low noise level. A bonus of our very short exposure time (around 0.5 seconds) is that dark current doesn't have a chance to build up to appreciable levels -- which means that we do not need to cool the chips! Hooray! As you might imagine, that simplifies the engineering and lowers the cost of the device considerably.
Now, one chip covers only a small region of the sky,
so in order to carry out an efficient survey, we need to combine many chips. The camera is still under construction, but a prototype of just a portion of it should give you some idea for the scale:

In this test device, eight CMOS chips are placed end-to-end to make one long column. Most of the locations of this test device are empty, as we are still acquiring sensors.
Q: Do you notice anything strange about this focal plane?
Yes, as you may have noticed, the focal "plane" is not flat, but slightly curved. It resembles the focal plane of another camera you may recognize:

Image courtesy of NASA and Ball Aerospace
Q: In what spacecraft does this camera work?
The answer is -- Kepler!
Why are these two cameras built on (very, very carefully) curved surface, instead of lying flat like a regular camera? It's a consequence of their optical design: because these devices are intended to cover a very wide area of the sky in a single shot, they have been placed at the focus of a special sort of telescope: a Schmidt camera.
A Schmidt camera is a telescope with some unusual optical design choices, made in order to boost its ability to survey large areas of the sky quickly:
How does it achieve these goals? Look at the diagram below:
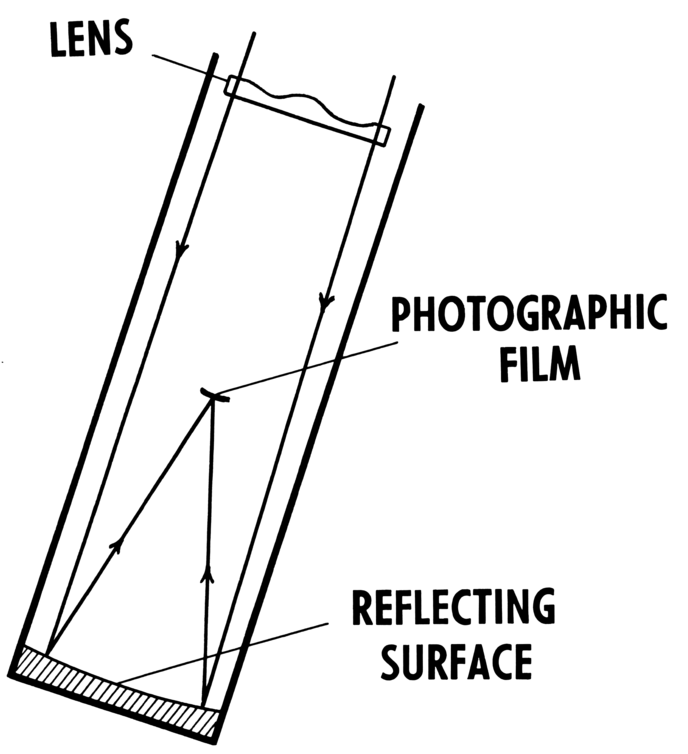
Image courtesy of Pearson_Scott_Foresman and Wikipedia.
There is one easy part, and two hard parts. The easy part is the spherical mirror, which can be fabricated relatively cheaply; a good thing, too, because the fast focal ratio means that the mirror has a more strongly curved surface than that of ordinary mirrors. The hard parts are the corrector lens at the front of the tube and the curved focal plane INSIDE THE TUBE .
Yes, that's right. Light comes to a focus inside the tube. That means that any human wishing to see the view would have to sit inside -- which is not going to happen. These telescopes are called "Schmidt CAMERAS" for a reason: they can't accomodate eyepieces at all. We'll return to discuss a consequence of this awkward location of the focal plane in a moment.
Tomo-e will live inside the 105-cm Kiso Schmidt camera, located in the Kiso Observatory, at an altitude of 1130 m in the mountains of central Japan.
The dome reminds me a bit of the helmet of a warrior:

This camera is the largest ever made by Nikon (as far as I know). I can impress my photographer friends by telling them that I use a pretty big telephoto lens: the focal length is 3300 mm :-)

As I mentioned earlier, one of the problems with Schmidt cameras is that they bring light to a focus inside their tubes. In the old days, when astronomers used photographic plates, that meant that after each exposure, one of the observatory staff members had to open a hatch and reach into the tube to take out the old plate and put in a new one:

These days, since the detectors are electronic, wires can carry the data recorded in each exposure to the outside world. Phew. But -- what if we want to change filters?
Q: What mechanism do you use to change filters
in YOUR cameras?
Q: Could a similar mechanism be used for Tomo-e?
The problem with placing a filter wheel inside the tube is that it would block some of the light entering the telescope.
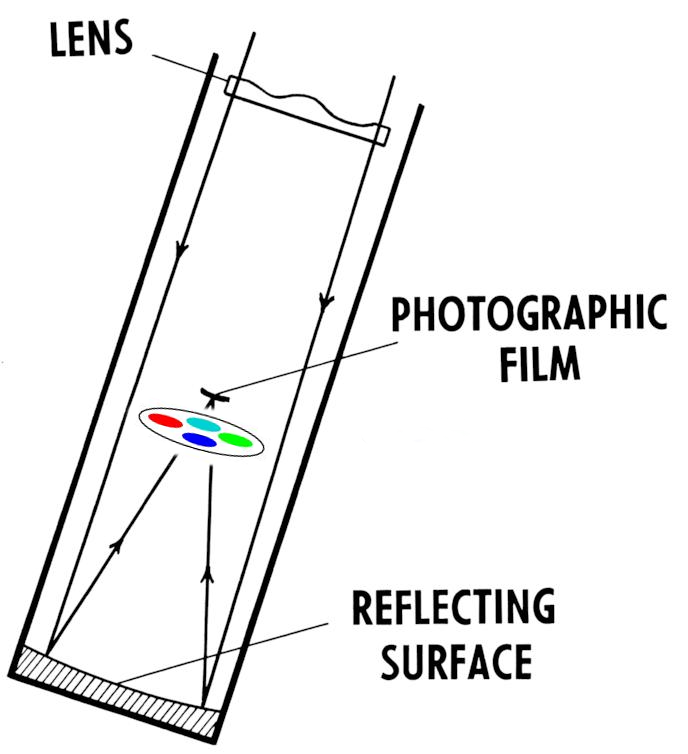
Image courtesy of Pearson_Scott_Foresman and Wikipedia.
modified by me.
Argh. How in the world can we change filters without blocking any light, and without having to open up the tube and reach inside each time?
The answer is -- ask a robot who lives INSIDE THE TUBE to do it for us! Tucked into a little alcove in the side of the tube is a robot arm made by Mitsubishi. Most of the time, it sits folded up, safely outside the path of light entering the telescope. But when it's time to change filters, it springs into action, grabbing the current filter, placing it into a box attached to the side of the tube, pulling out the new filter, slide the new one into place, and then going back to its resting position. (Click on the image below to start a short animation)
The benefit of using a Schmidt camera is the very wide field of view it provides. That means that instead of a single chip, we can place a LOT of chips on the (curved) focal plane.

Image taken from
a presentation by Shigeyuki Sako
There will be some vignetting near the edges of the field, and there are gaps between the chips, but the area this camera can cover is huge!
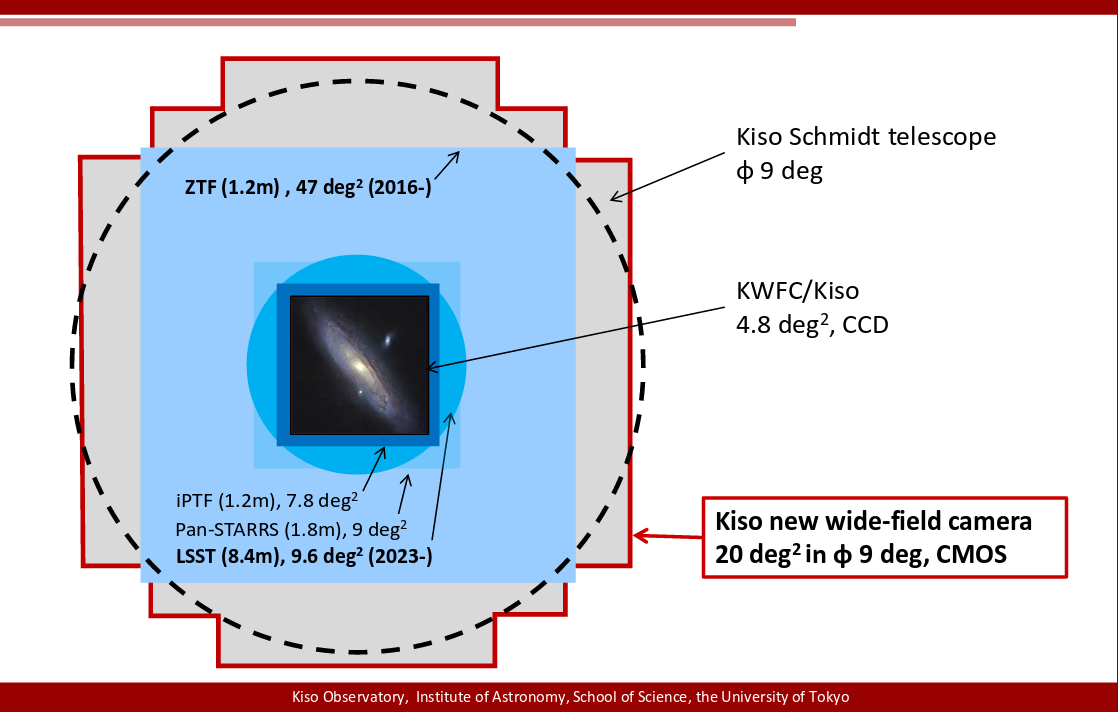
Of course, the large area covered by each exposure means that there's a lot of data to transfer and store and analyze, too:
Total pixels: 190 million
One exposure: 380 MBytes (16 bits per pixel)
If exposure time is 0.5 seconds, then
Data rate: 760 Mbytes/sec = 2.7 TBytes/hour
~ 20 TBytes/night
Since my role in the project is to write software which analyzes the images, and since we want to detect transient objects soon after their light enters the telescope ... I have a tough job :-/
Our main focus is on finding brief, transient events in the sky. As described earlier , very brief flashes of light will appear brightest in very brief exposures; in the long exposures typical of most astronomical surveys, they will be increasingly swamped by noise and become harder to detect.
Of course, these events are thought to be rare. In order to find them efficiently, one must search a very large area of the sky. Therefore, one way to estimate the ability of a survey to find transient sources is to combine its field of view with the time scale of its exposures.
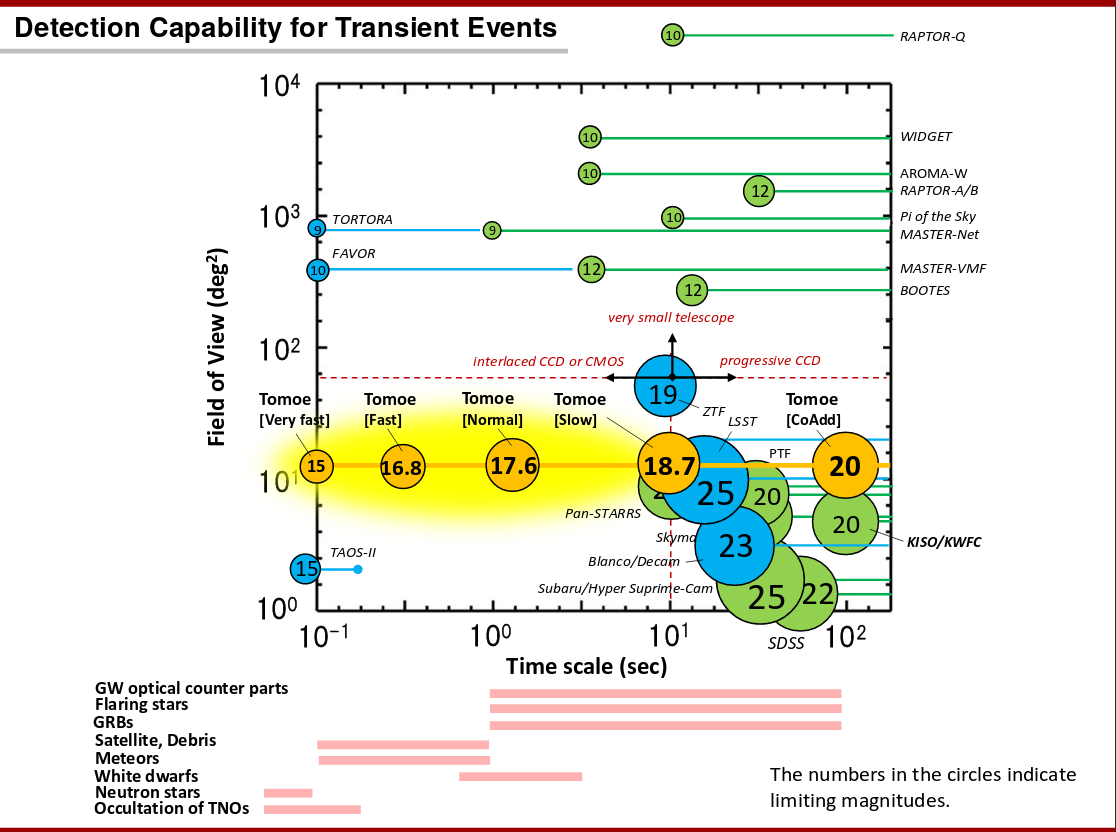
Image taken from
a presentation by Shigeyuki Sako
In practice, there are several strategies we could take in the operations.

Image taken from
a presentation by Shigeyuki Sako
The Tomo-e Gozen camera is still under construction, and won't be completed for some time. However, a prototype has been used to gather test data on the Kiso Schmidt camera since 2016, and more test observations are scheduled for this coming winter season.
Let me show you a short movie of the images gathered by a single chip during the night of April 11, 2016. This region of the sky is about 39 x 22 arcminutes in size. To start, let's examine a single frame:

How faint are the objects shown in this picture? Well, compare it to the same area of the sky as shown in the Digitized Sky Survey, thanks to Skyview. Below is a scan of a photograph taken with the UK Schmidt camera, which is slightly larger than the Kiso Schmidt (120 cm vs. 105 cm in diameter). This photograph required an exposure time of one hour = 3600 seconds, compared to the 0.5 seconds for the Tomo-e image. (Click on the image to compare Tomo-e to the photograph)
The photographic plate records objects as faint as V=20 or so, while Tomo-e only reaches objects down to around V=16.5. One reason for the difference is the relatively poor seeing in the Tomo-e image: the typical FWHM at Kiso is around 2.5 to 3.5 arcseconds, while the photographic plate has a FWHM of only about 1.0 arcseconds. Oh, and, of course, the photographic plate was exposed for 7200 times longer than the CMOS chip.
Now let's look at a movie, made up of 360 individual images, each 0.5 seconds long. In real time, this recording shows 180 seconds of continuous data; however, I've sped it up by a factor of 12 for this presentation, so it lasts just 15 seconds. (Click on the picture to see the movie)
Q: Do you see any brief flashes of light? Q: How many? Where?
Great! Well done! Nice eyes!
Unfortunately, all those flashes are artificial stars that I inserted into the real images to test our transient-finding software. By finding all of them, you have proved yourself to be expert flash-finding detectives.
During my recent visit to the National Astronomical Observatory of Japan, I analyzed eight nights of Tomo-e images to look for transient sources. Despite the large volume of data -- covering about 200,000 square-degree-seconds, or the equivalent of one square degree monitored for about 55 hours -- we did not find any flashes of light lasting between 1.5 and 10 seconds. We would have seen such flashes if they had produced each second as much light as a star of magnitude V=15.
So, apparently, the optical counterparts of gamma-ray bursts and fast radio bursts and very young supernovae are .... not so easy to find. This is no surprise: it is consistent with the rates estimated by other astronomers. That's why we are building the full camera, with many more chips, and planning to scan the sky for many months and years to come.
In March, 2018, the MAXI X-ray telescope and the optical All-Sky Automated Survey for SuperNovae (ASASSN) noticed a source not far from the celestial equator which suddenly grew much brighter than normal. This object showed large changes in brightness on short timescales in both wavelength ranges. I made a few measurements myself with the 12-inch telescope at the RIT Observatory, but it was difficult: the variations were clearly shorter in time than my 5-second exposures could resolve.
The Tomo-e Gozen team did a much better job, because the instrument is designed to take short exposures. You can see some examples of their measurements at
Click on the image below to see a version at full size, which shows clearly the variations on timescales of tenths of a second.
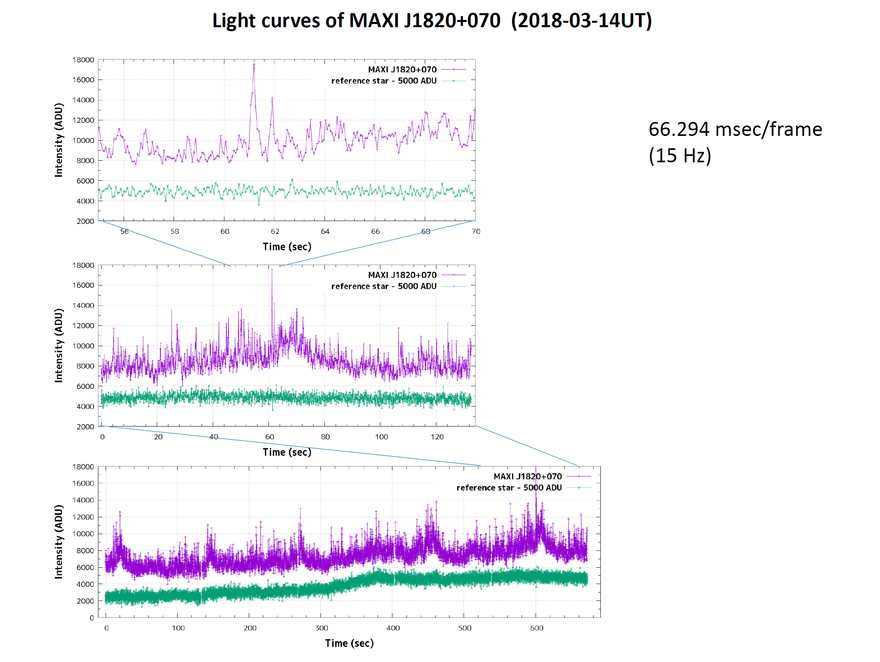
Image courtesy of
the Tomo-e Gozen project