
Image courtesy of Stephan Hamel and Wikimedia
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomers see a wide variety of gas clouds in space. Some block the light of stars behind them; other glow brightly in many colors. Today, we'll investigate one type of the glowing gas clouds: Stromgren spheres, named after the astronomer who first applied atomic theory to figure out their properties.
My goal is to explain the nature of these bright clouds, and answer questions such as "what makes them glow?" and "how large should they be?"
Contents
Let's start by looking at a few examples of Stromgren spheres. What common features do you see?
The Rosette Nebula, aka Caldwell 49, inside of which sits the open cluster NGC 2244.

Image courtesy of
Stephan Hamel and Wikimedia
The Spirograph Nebula, aka IC 418.
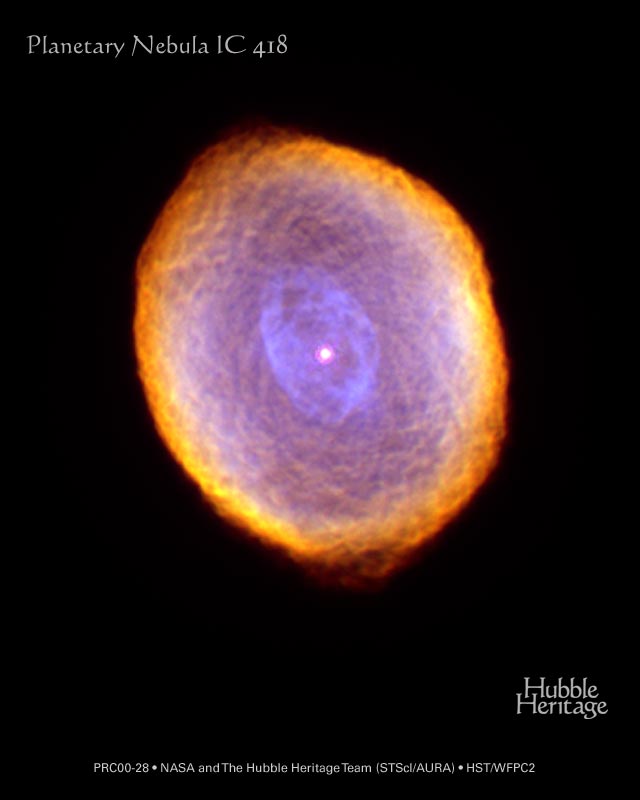
Image courtesy of
NASA and The Hubble Heritage Team (STScI/AURA)
and Dr. Raghvendra Sahai (JPL) and Dr. Arsen R. Hajian (USNO)
A set of very young stars in the Orion Nebula.
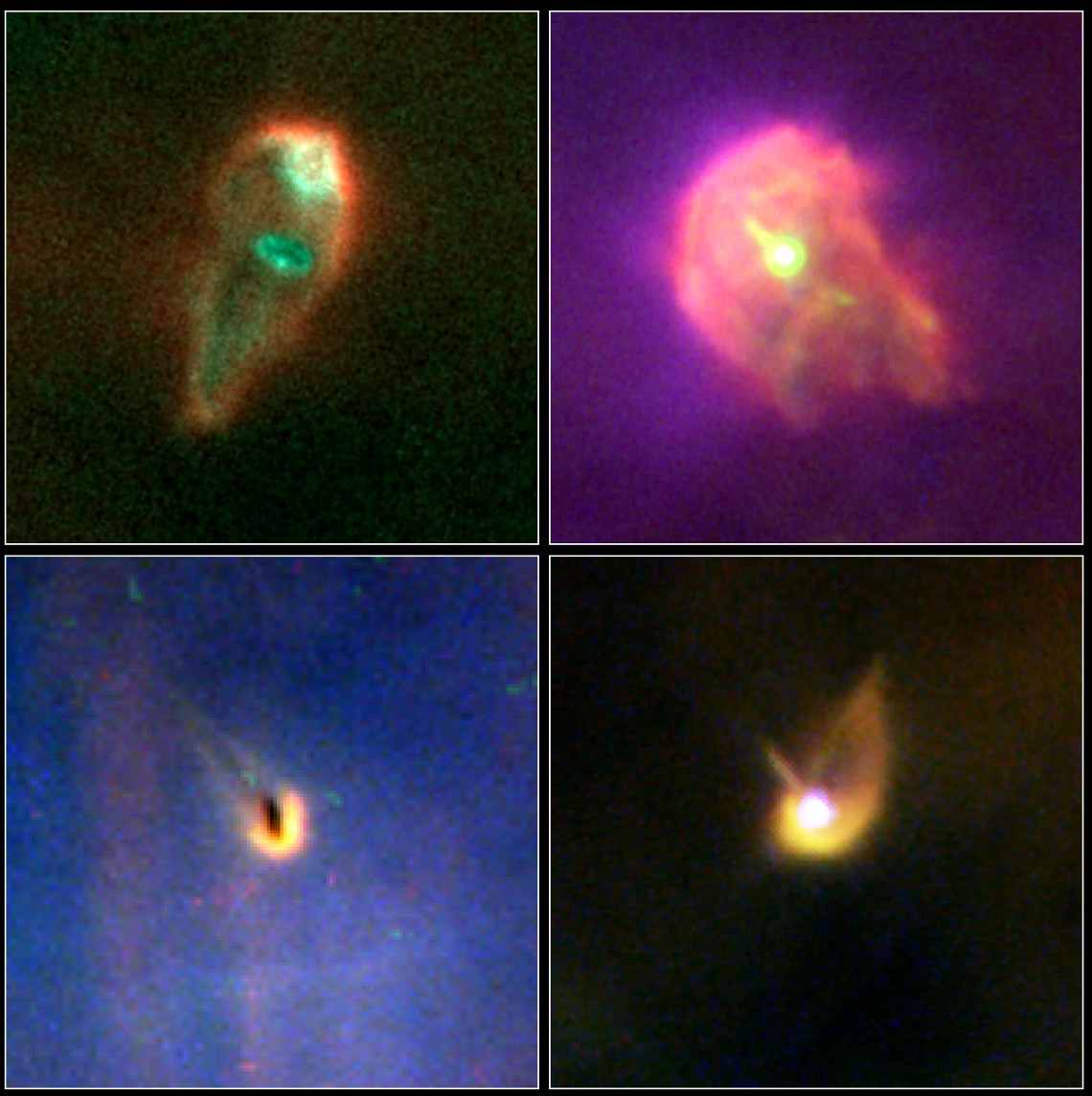
Image courtesy of
NASA, ESA, J. Bally (University of Colorado, Boulder), H. Throop (Southwest Research Institute, Boulder), and C. O'Dell (Vanderbilt University)
Q: What common features did you see in all these examples?
I would say that all the examples include
So what's going on here?
The name "Stromgren" is attached to these objects because their properties were first explained in depth by the Danish astronomer Bengt Stromgren.
It's no surprise that Stromgren became an astronomer, as he grew up in this building, the Ostervold Observatory in Copenhagen, Denmark.

Image courtesy of
Olivier Bruchez and Wikimedia
His father, Svante Elis Strömgren, was appointed as the Professor of Astronomy at the Copenhagen University. Bengt, born in 1908, studied under his father's tutelage, learning advanced mathematics at an early age. He published his first paper, on the positions of a comet, at the age of 14. Bengt took a job as a laboratory assistant at the Institute for Theoretical Physics, run by Neils Bohr. It's pretty clear that he was a smart cookie. Eventually, he was named a professor at the University of Copenhagen and replaced his father at the observatory.
In 1939, he published a very influential paper describing the interaction of ultraviolet photons from hot stars with atoms in the nearby interstellar medium. Ever since, the glowing regions around hot stars have been called "Stromgren spheres" in his honor.
In addition to his theoretical work, he was also a talented observer. He devised a system of filters with intermediate widths and wavelengths tuned to the locations of important features in stellar spectra. The "Stromgren photometry" based on these filters has been used for decades to classify stars much more cleanly than measurements made in other passbands.
He was invited to become Directory of the Yerkes Observatory, and lived in the US for several years.

Photograph of astronomers at Yerkes Observatory in 1937,
courtesy of
"Bengt Strömgren: Interstellar Glow, Helium Content, and Solar Life Supply, 1932–1940,"
by Simon Rebsdorf (Centaurus, 49, 56 (2007)).
Stromgren is the large man in center of the front row.
Can you name any others?
Check for answers ...
In 1957, he left Yerkes to take a position at the Institute for Advanced Study in Princeton, NJ. His took over the office last used by some fellow named Einstein (who had died two years earlier). Ten years later, he moved back to Denmark with his family, where he continued to perform research until his death in 1987.
In order to understand why hot stars create glowing spheres of gas from the clouds which surround them, we need to review some of the physics of the interactions of photons with hydrogen atoms. This will be a very simplified view.
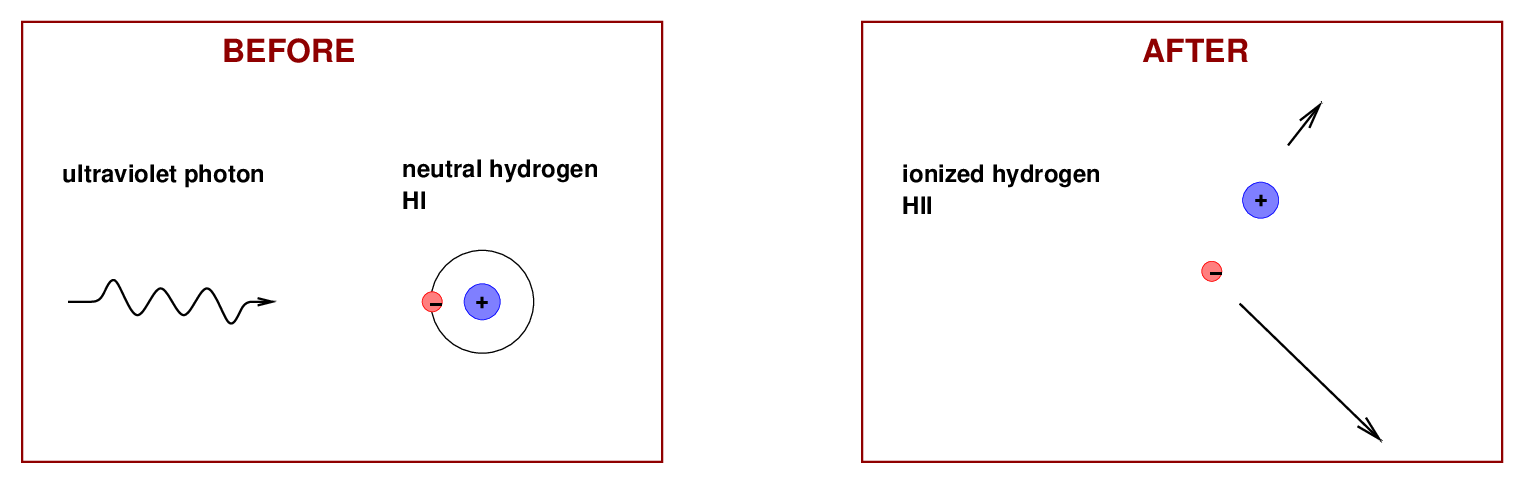
We will be concerned with two physical processes. In the first, a high-energy ultraviolet photon runs into a neutral hydrogen atom (which astronomers call "HI", pronounced "H one") and ionizes it: it knocks the electron out of the atom completely, separating the positively charged proton and negatively charged electron. Those two particles fly off in different directions, turning into an ionized gas which astronomers call "HII" (pronounced "H two").
The second process we need to discuss is the reverse: one electron, and one proton, each wandering alone through space, run into each other and recombine to form a neutral hydrogen atom. When the atom forms, it generally has an excess of energy, which it releases in the form of one or more photons.
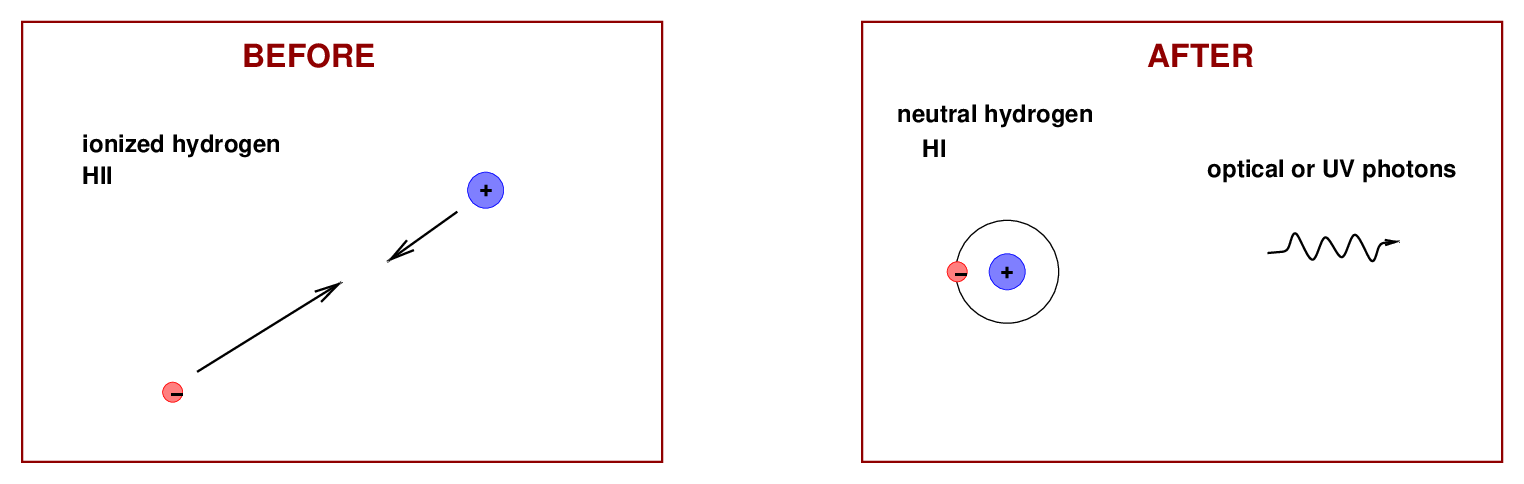
Many of the photons produced in this manner have a very pretty deep-red color, as you will recognize from many photographs of glowing nebulae.

Image of Orion Nebula on Kodak Ektachrome courtesy of
Bill Schoening/NOIRLab/NSF/AURA
Okay, that was the overview of what's happening. Let's look at the process in a bit more detail.
A hydrogen atom consists of a positive particle, the proton, sitting at its center; we call that the nucleus of the atom. Around the nucleus moves a negatively charged particle, the electron. The electron can only orbit the nucleus at very particular distances, which we can identify with numbers n = 1, 2, 3, ..., ∞ .
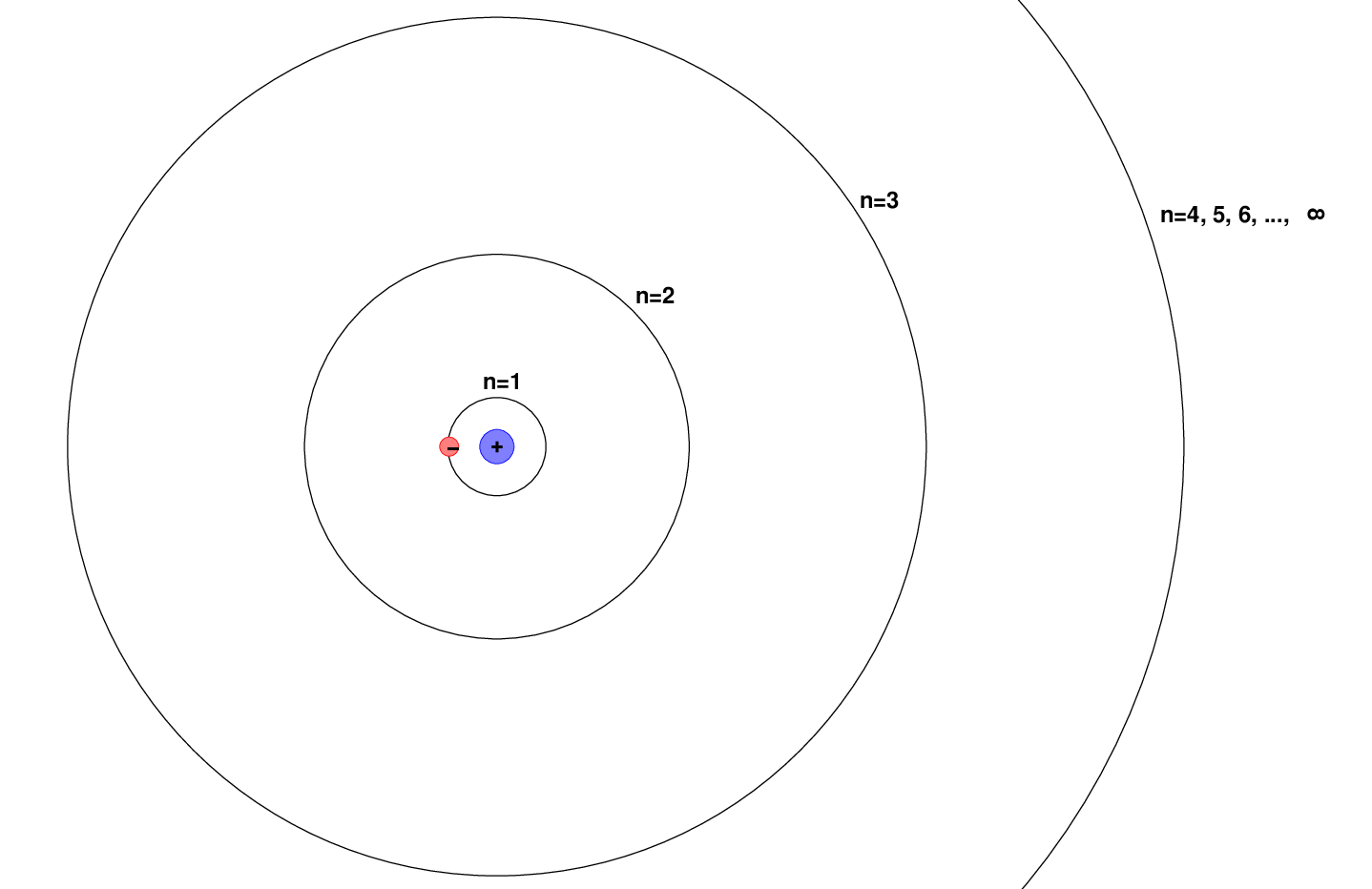
Each orbit has a particular energy associated with it. The "ground state", or state with the lowest energy, is the n = 1 orbit, closest to the nucleus. Larger orbits require the electron to have more energy. It turns out that there is a relatively simple formula relating the orbital number n to the energy of the electron.
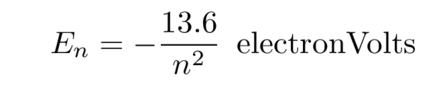
It often helps to create a pictorial schematic showing the energy levels within a hydrogen atom.
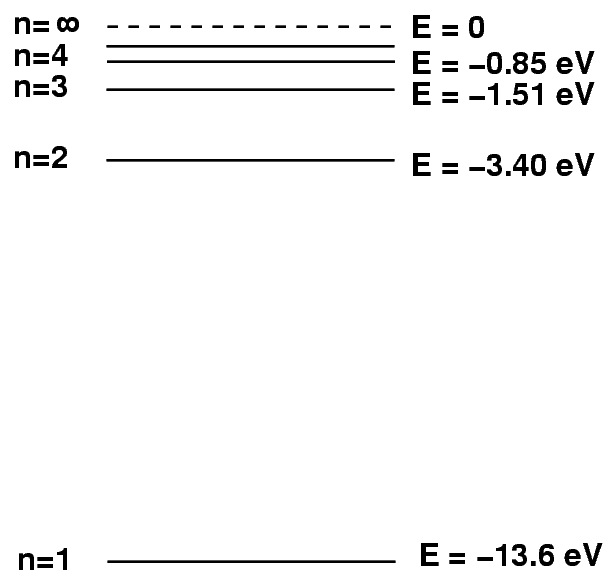
We can represent the electron dropping from a higher energy state to a lower energy state by drawing a picture in which a little red ball jumps down from one level to another. The difference in energy between starting and ending levels turns into the energy of a photon that the atoms emits as a result of this process.
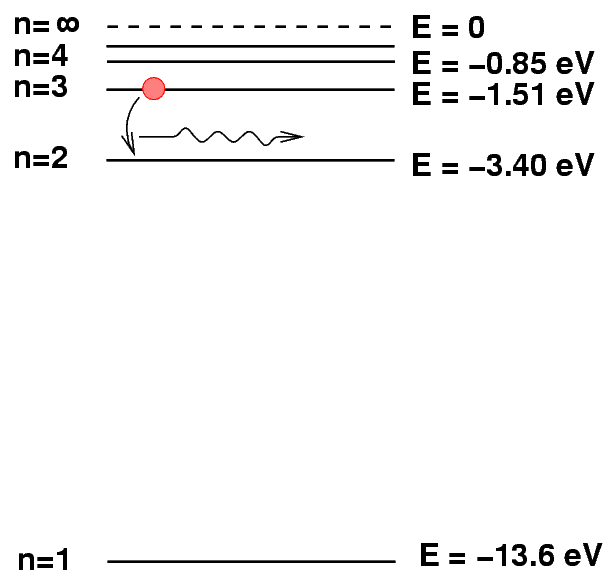
Q: What is the energy of the photon produced when a hydrogen
atom de-excites from n = 3 to n = 2?
You can convert the energy of a photon (in eV) to the wavelength of the photon (in Angstroms) by using the formula
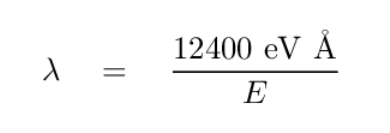
Q: What is the wavelength of the photon emitted by a hydrogen
atom when it de-excites from n = 3 to n = 2?
Q: What color corresponds to that wavelength?
Now, Stromgren spheres are produced when photons from a star ionize the hydrogen atoms in the surrounding region. As you'll recall, "ionizing" an atom means knocking the electron completely out of orbit, so that it leaves the proton behind and flies off into space alone.
In the great majority of atoms, the electron sits in its lowest energy level, n = 1. In order to knock the electron free, the incoming photon must have at least enough energy to raise the electron from n = 1 to n = ∞. Just how much energy does this take?
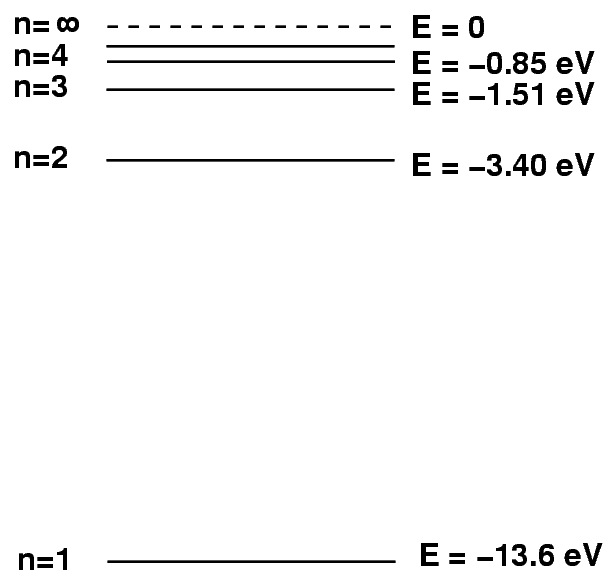
Q: Just how much energy does it take to raise the electron
from n = 1 to n = ∞?
Can you figure out the wavelength of such a photon? It might help to remember this equation.
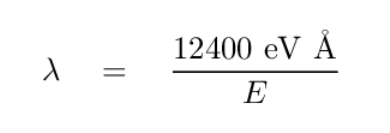
Q: What is the critical wavelength for a photon which
can ionize a hydrogen atom?
Right. Photons with wavelengths of 912 Å, or shorter, have enough energy to ionize hydrogen from the ground state. This critical value is sometimes called the Lyman limit, after Theodore Lyman, a physicist who studied hydrogen's spectrum in the early 1900s. This wavelength is much shorter than those visible to human eyes, which lie in the range from roughly 4000 to 8000 Å. It takes an ultraviolet photon to do the job.
Now, the Sun is a wonderful star, and responsible for keeping all of us alive on Earth, but it doesn't produce many photons with wavelengths this short. Why not? Because the Sun, like most main-sequence stars, emits light which has (at last approximately) a blackbody spectrum: a distribution of energy which falls off very sharply at short wavelengths.
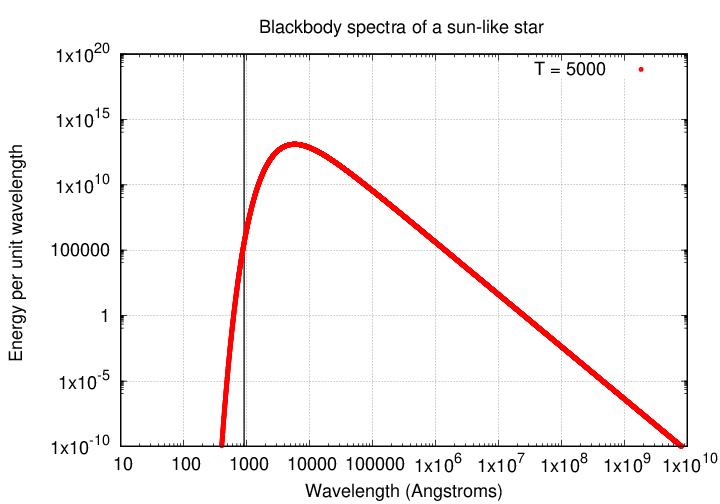
Note that the y-axis is logarithmic, so one must read values from the graph carefully. At the peak of the spectrum, around 5000 Å, the Sun emits MUCH more energy than it does at the Lyman limit.
Q: Estimate the ratio of energy emitted at 5000 Å
to that emitted at 912 Å in the solar spectrum.
In short, the Sun is not a good source of ionizing photons.
However, stars which are much hotter than the Sun do produce a larger number of high-energy, ultraviolet photons. In fact, the spectrum of an O star of temperature 50,000 Kelvin reaches its peak at a wavelength even shorter than 912 Å.
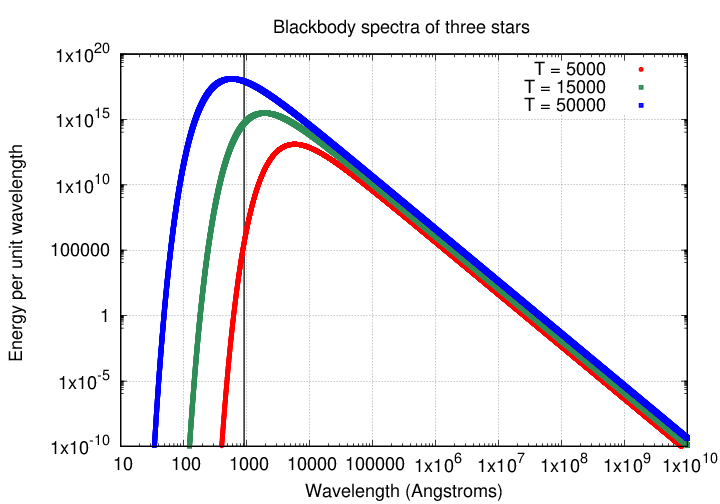
To sum things up, the answer to "What does it take to ionize a hydrogen atom?" is, to a large extent, "a very hot star."
Since ultraviolet photons are so important to our story -- an explanation of Stromgren spheres -- let's take a moment to investigate the number of these ionizing photons produced by different types of stars. If we pretend that ordinary stars emit light with a blackbody spectrum, which isn't a terrible approximation, then we can use a couple of mathematical formulae to work out the number of these UV photons they emit each second.
First, as first described by Max von Planck in the year 1900, the amount of energy emitted as a function of wavelength λ by one square meter of an object of temperature T is
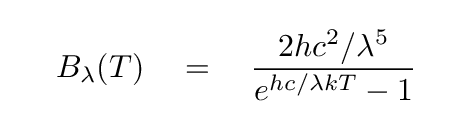
where c is the speed of light, k is the Boltzmann constant, and h is (quite properly) Planck's constant. Since there's a simple relationship between the energy of a photon and its wavelength,
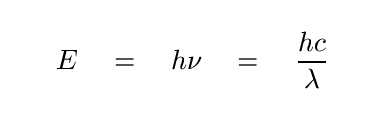
we can convert the energy emitted by each square meter of a blackbody into the number of photons emitted at each wavelength, and count those which have wavelengths shorter than 912 Å.
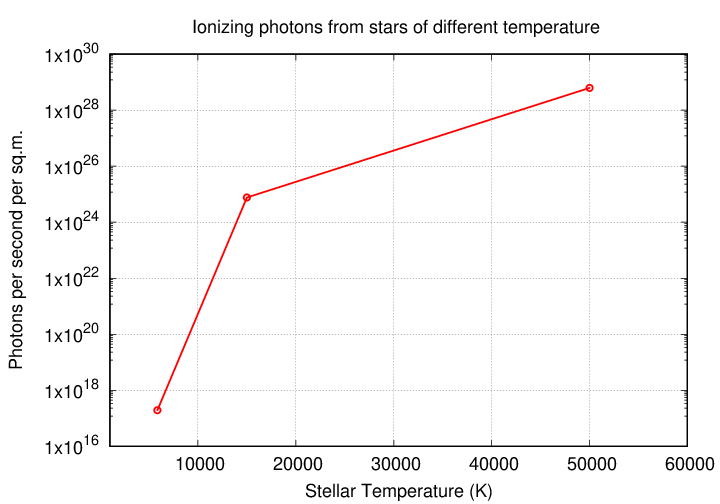
Let's compare three stars, all on the main sequence: a low-mass G2V star like the Sun, a more massive B5V star with a mass 6 times that of the Sun, and a very rare O5V of perhaps 60 or 65 solar masses.
spec type temperature number of ionizing
(K) photons per sq.m. per sec
---------------------------------------------------------------------------
G2V 5860 1.96 x 1017
B5V 15000 7.63 x 1024
O5V 50000 6.23 x 1028
------------------------------------------------------------------------
But wait -- there's another difference between these stars. It's not only the temperature which increases with mass along the main sequence; the size of the star grows larger with mass, too.
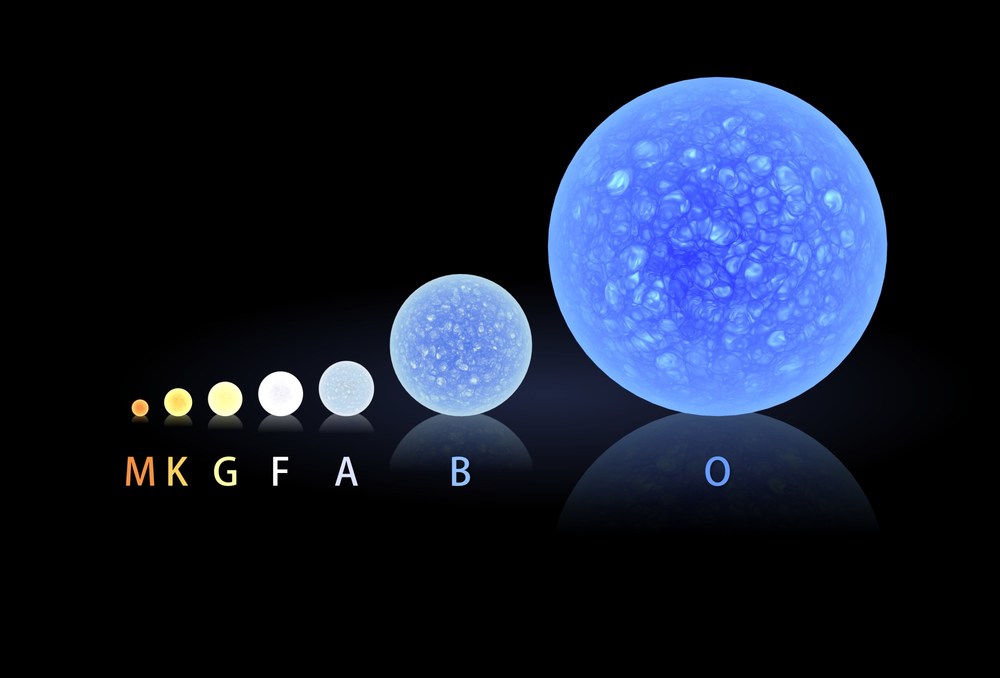
Image courtesy of
NASA’s Goddard Space Flight Center
And if the radius of an O5V stars is larger than that of the Sun, it has a lot more square meters of photosphere. Each one of those square meters emits many more UV photons than each square meter of the Sun's photosphere. When one combines the effect of size with that of temperature, the difference in the number of ionizing photons becomes downright ginormous.
spec type temperature radius number of ionizing
(K) (m) photons per sec
---------------------------------------------------------------------------
G2V 5860 6.96 x 108 1.9 x 1037
B5V 15000 2.78 x 109 7.5 x 1044
O5V 50000 1.11 x 1010 9.7 x 1049
------------------------------------------------------------------------
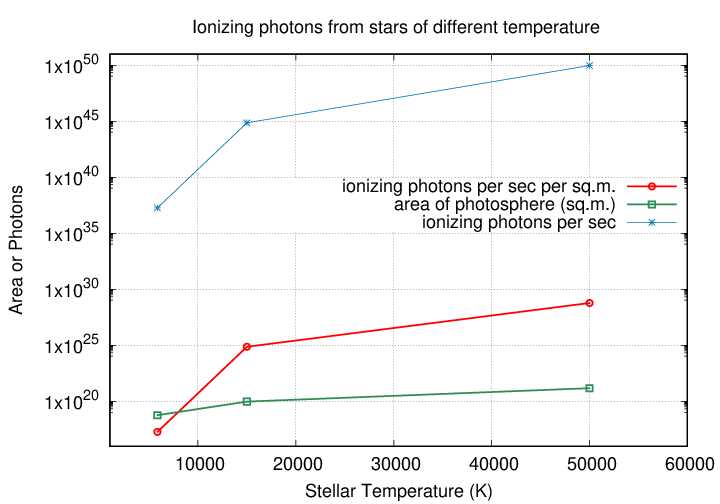
Wow. The O5V star produces roughly SIX TRILLION times as many ionizing photons as the Sun-like star. Surely it will produce a more impressive cloud of glowing hydrogen around itself ... but, well, how MUCH more impressive?
We've established that a star emitting ultraviolet photons with wavelengths less than 912 Å will ionize the neutral hydrogen atoms (HI) in the region around the star, creating a volume filled with ionized hydrogen gas (HII). Particles in the ionized region will occasionally combine to form hydrogen atoms, emitting light -- including red visible light -- as their electrons jump down to the ground state. The picture looks like this:
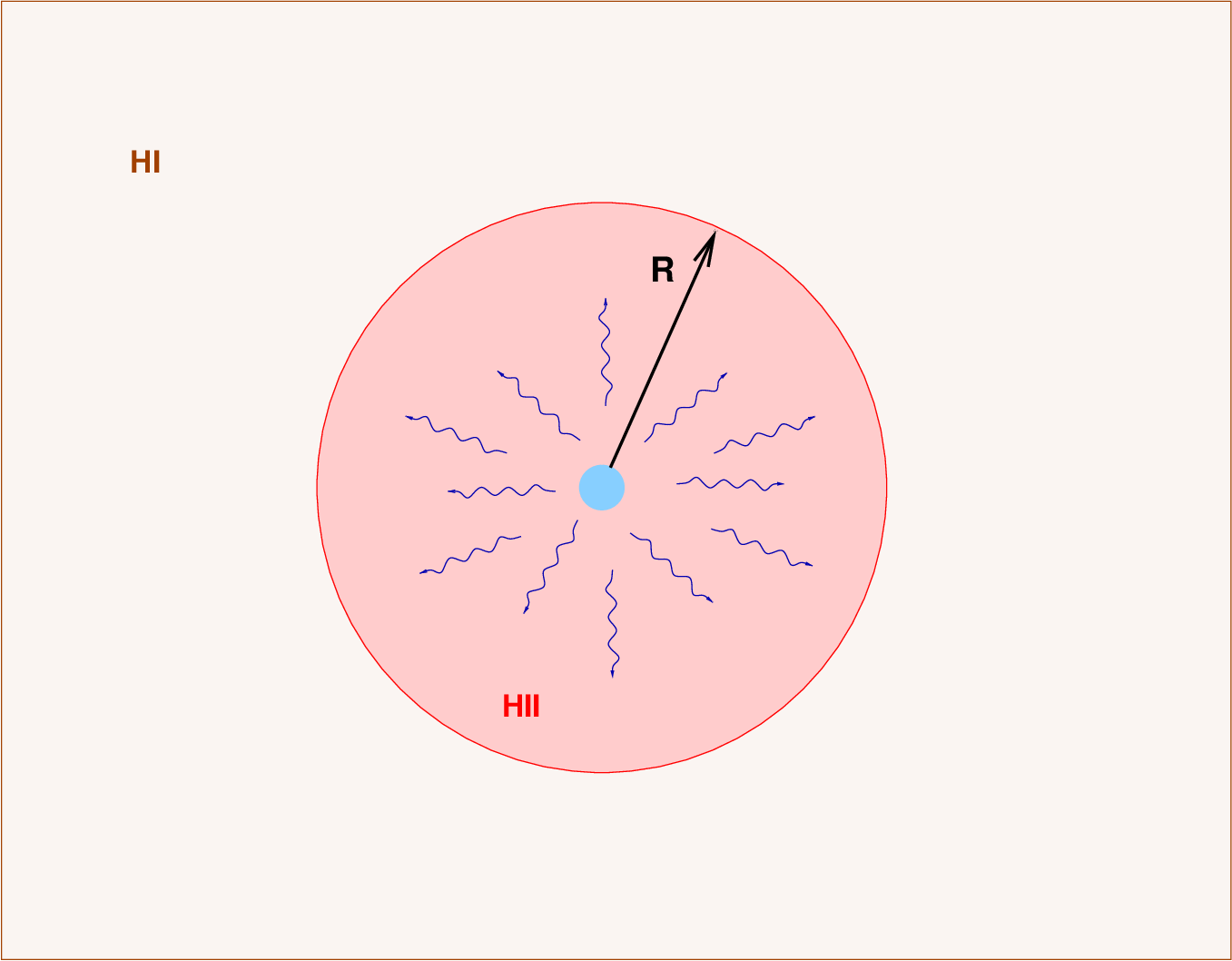
The question is -- how large will this "Stromgren sphere" be? What is the radius R? And how does this radius depend upon properties of the central star?
This is a complicated question. There's a reason that Stromgren's 1939 paper runs for 22 pages! In the real universe, these regions around hot stars are very active: in some places, the ionized region might shrink as a cloud of dense gas passes by; in other places, the region might expand a bit due to a flare from the star. We'll adopt a very simple, not very realistic, model: one which is completely static and in a steady state. The star emits a constant number of ultraviolet photons, the gas sits still and absorbs the photons.
In this simplified model, we need to find the radius R which brings two processes into a balance:
If the sphere is too small, then it can't contain enough atoms to absorb all the photons emitted by the star. On the other hand, if the sphere is too big, all the photons will be absorbed before they can reach the outer reaches of the sphere. We need to find the radius which is ju-u-u-st right.

Astronomers -- led by Stromgren -- put these ideas into an equation:
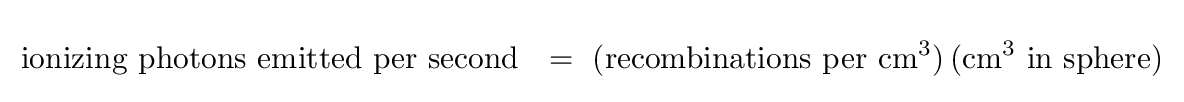
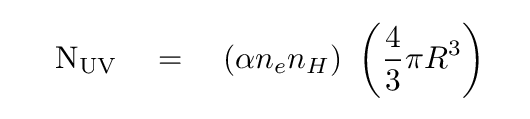
On the right hand side, the items in the first term might need some explanation. ne and nH are the density of electrons and protons per cubic centimeter, respectively, inside the ionized region; this way of writing those values assumes that all the hydrogen atoms are ionized, which is not quite true, but close enough for us. The symbol α describes the rate at which electrons and protons combine to form hydrogen atom. Clearly, the denser the region is, the larger this term will be.
We can re-arrange this equation to solve for the radius of the sphere R.
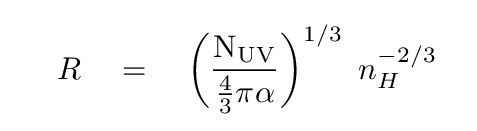
I'll provide some representative values for you to use ...
Q: A massive O5V star emits NUV = 9.7 x 1049 ionizing photons
each second. How large might its Stromgren sphere extend?
(look below to compare your answer to Stromgren's)
Q: The puny Sun emits only NUV = 1.9 x 1037 ionizing photons
per second. What is the size of the Sun's Stromgren sphere?
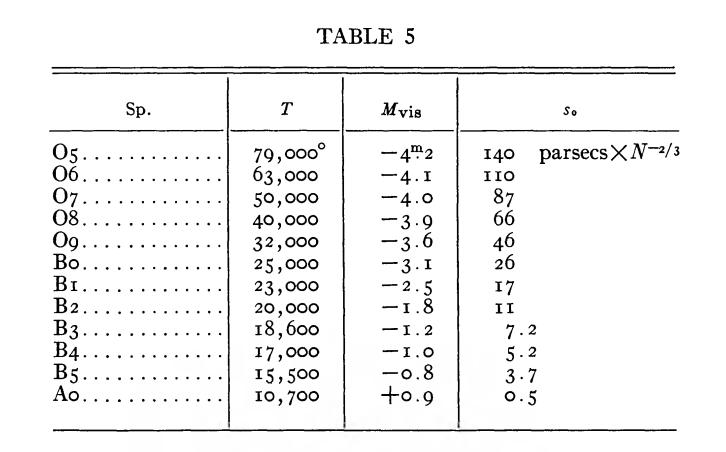
In Stromgren's 1939 paper, he assumed the the density nH = 1 per cm3 to derive these values:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.