
Contents
A recent issue of the ASRAS newsletter includes this item, recounting a story from its archives.

Hmmm, I thought. That doesn't sound quite right. Only 27 days?
Let's take a look at this problem, and see if we can figure out the solution. Perhaps there has been a miscarriage of justice .... if so, we need to set the record straight.
There are a number of ways to solve this problem, but I think one of the more intuitive calls upon a relationship between the size of an orbit and its period. This connection was first written down by a dude named Kepler.

XKCD comic 21
is written by Randall Munroe.
Johannes Kepler realized -- after studying the motions of the planets in the Solar System for decades -- that there was a simple relationship between the period and size of each planet's orbit. The version you will see in textbooks today includes a few bits and pieces which were added later, such as G, the constant of universal gravitation.
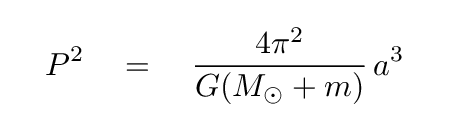
But we'll stick with a simpler version, which is closer to the one found by Kepler, and will do all the work we need to solve our puzzle.
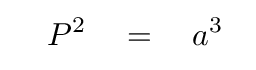
Here,
I hope that you know what a year is. But the term "semi-major axis" might be a bit confusing. Let's look at what that means, using the Earth's orbit as a reference.
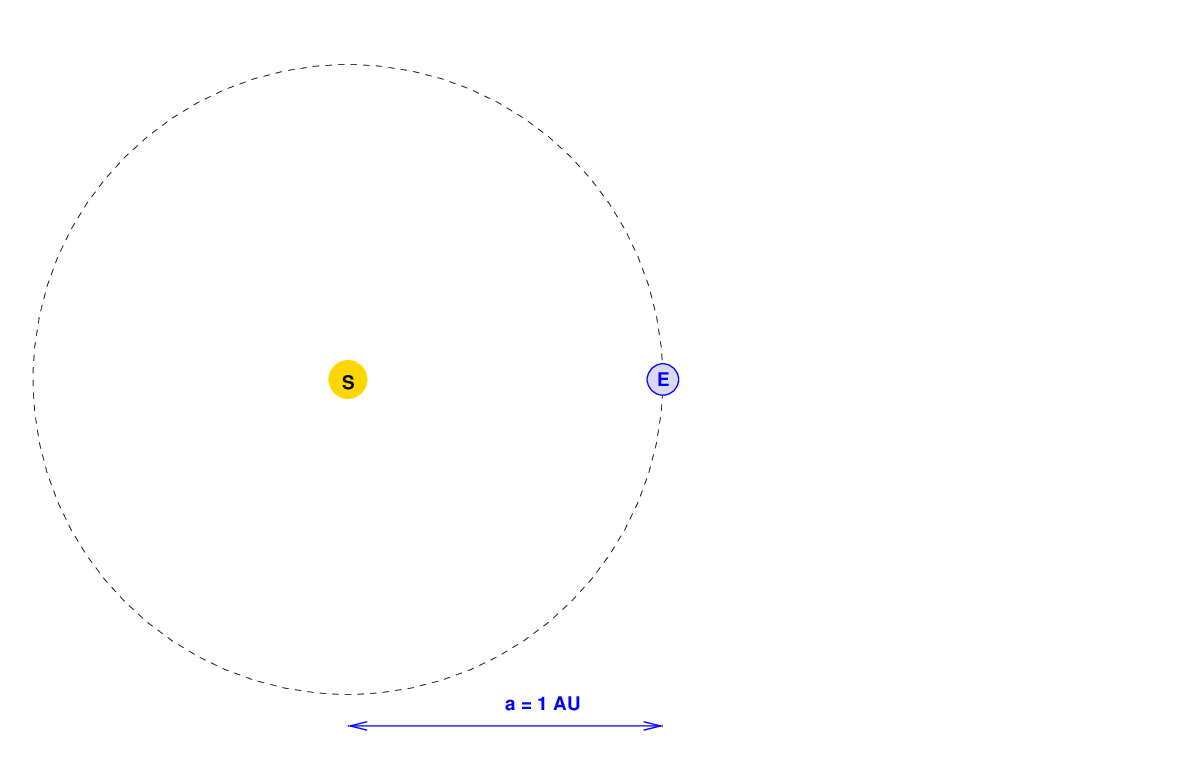
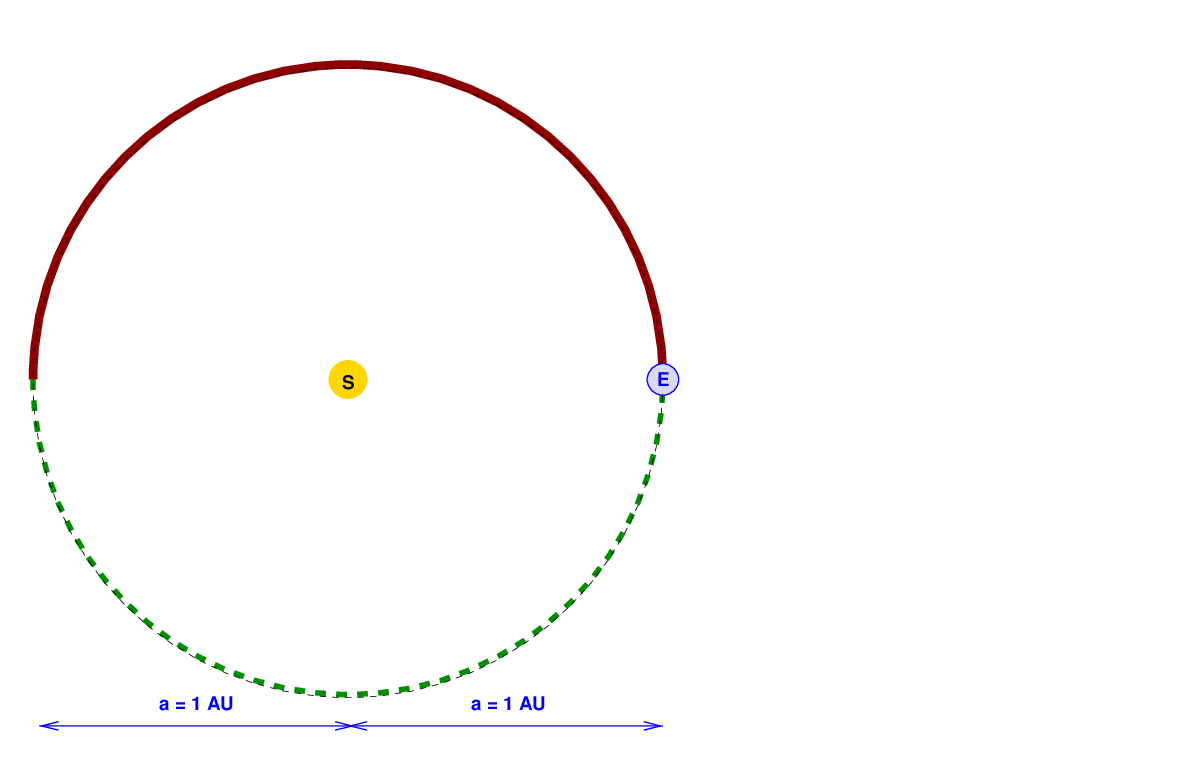
For a circular (or nearly circular) orbit, like the Earth's, the semi-major axis is simply the radius of the orbit: the distance between the Earth and the Sun. We define the Astronomical Unit (or AU for short) as the distance between the Earth and the Sun, so this semi-major axis a is equal to exactly 1 AU. Easy-peasy.
If we wanted to make it a bit more complicated, we could define things this way.
That's kind of silly for a circular orbit.
But let's pick an orbit which is not circular, but has some eccentricity. In that case, the orbit is an ellipse in which the major axis is larger than all other straight lines across the orbit. If a spaceship followed the brown solid line in the diagram below, it would at some times be very close to the Sun -- and move very fast -- and at other times very far away -- and travel very slowly.
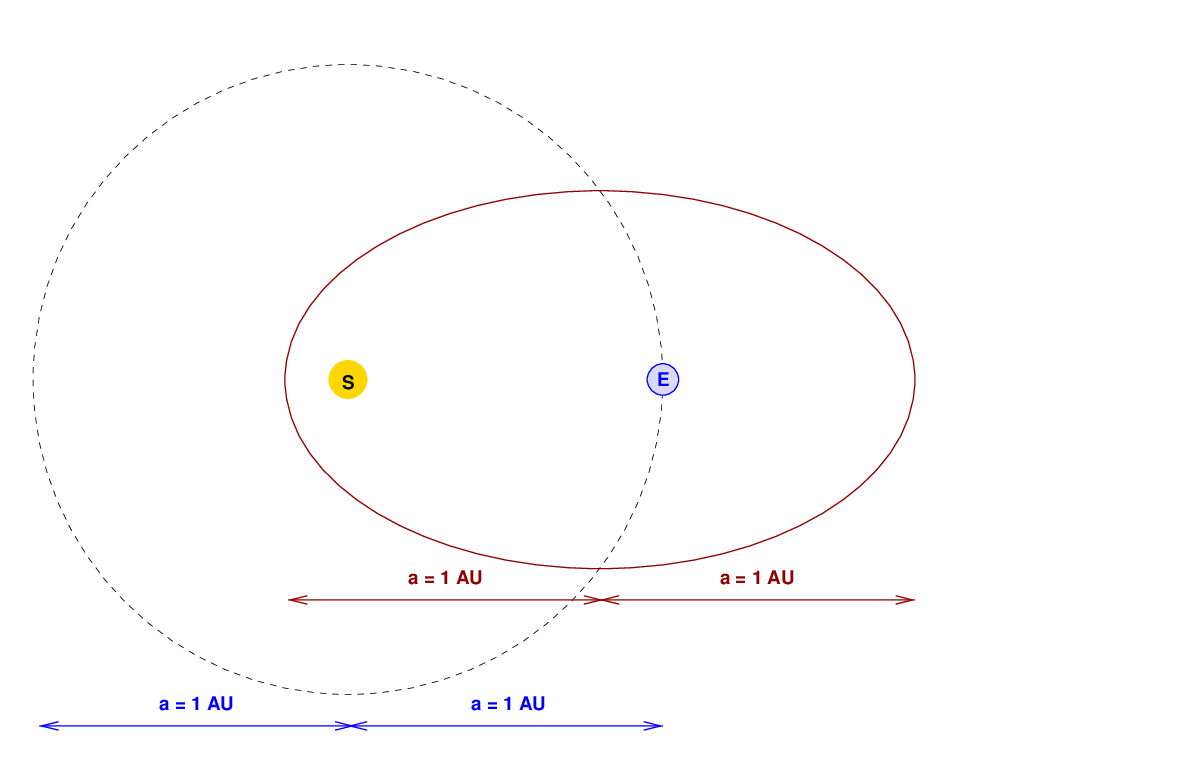
Notice, however, that the major axis of the brown orbit is the same length as the major axis of Earth's orbit; and so the semi-major axis a of this brown orbit is the same as that of the Earth's orbit: exactly 1 AU. According to Kepler's Third Law,
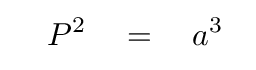
the spaceship on its elliptical orbit would have exactly the same period as the Earth on its circular orbit: one year.
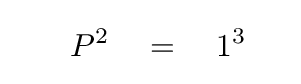
This period would remain the same for an even more eccentric orbit. As long as a = 1 AU, the period will be 1 year.
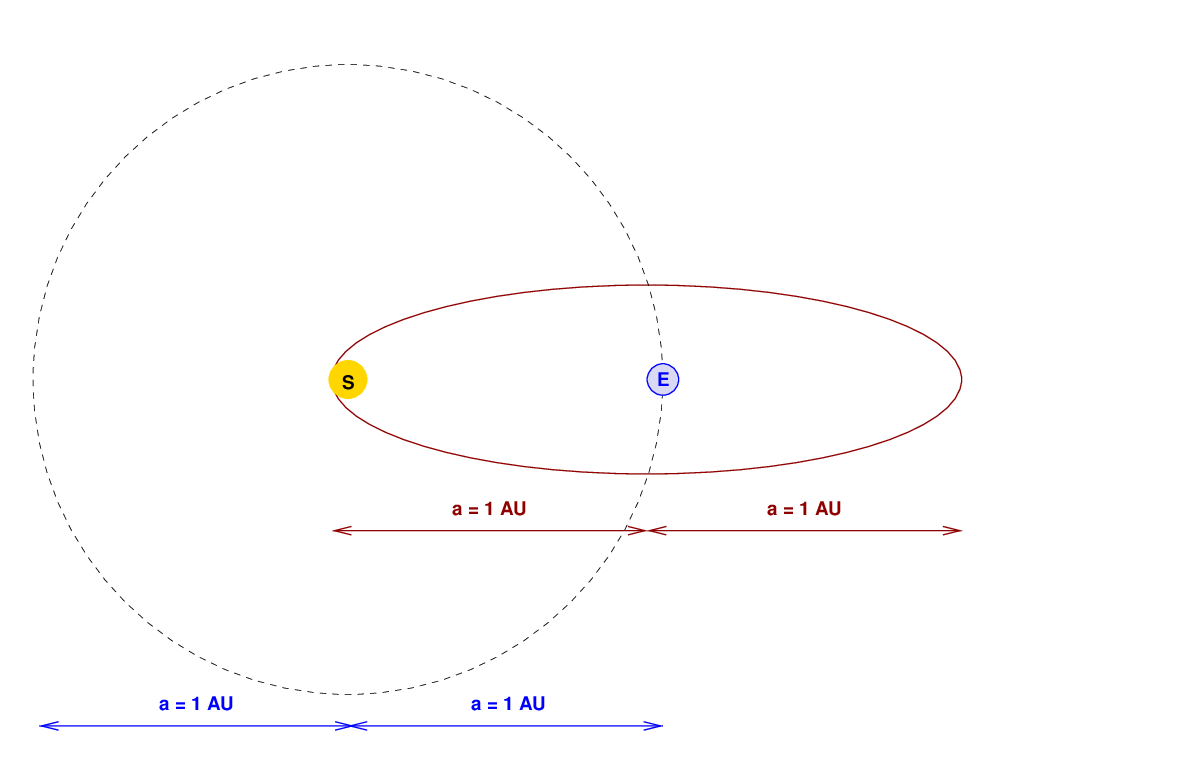
Okay, so we've established that the period of an orbit depends only on the semi-major axis; it doesn't matter how circular or how eccentric that orbit is, it must follow Kepler's Third Law. Fine.
But suppose we change the semi-major axis? For example, what would happen if we made an orbit which is just HALF the size of Earth's orbit?
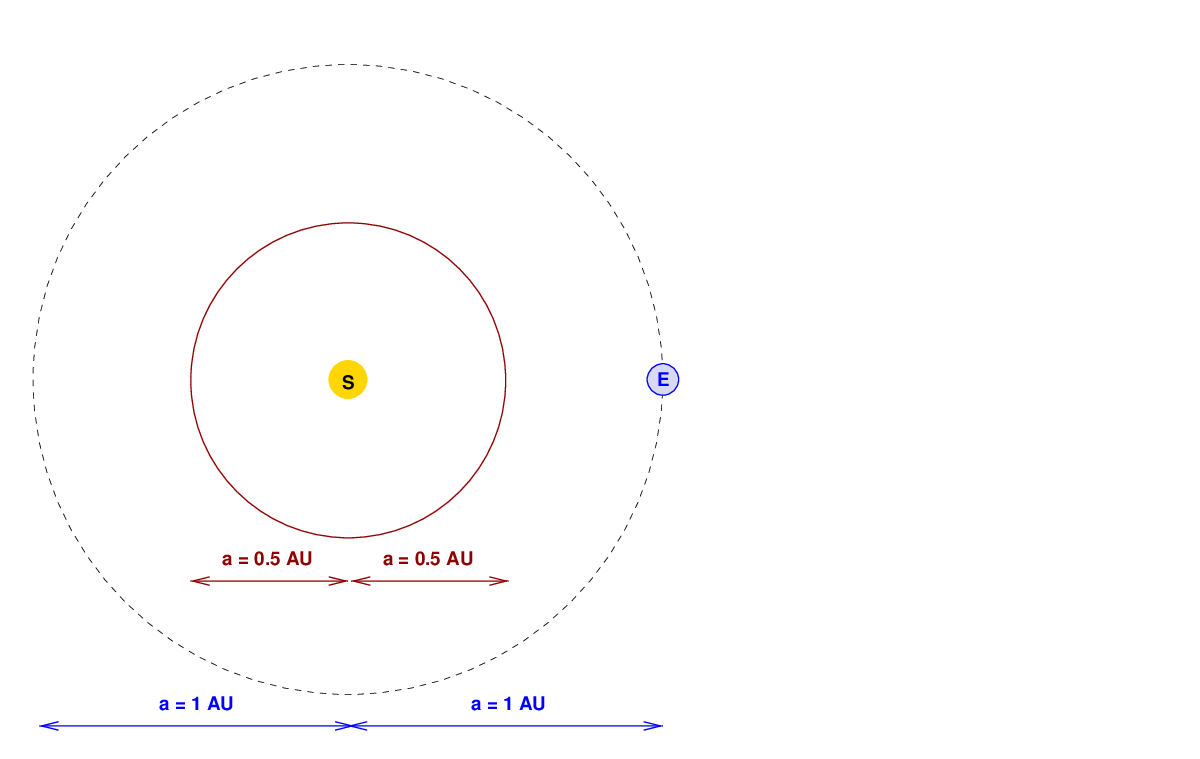
Well, now the semi-major axis a = 0.5 AU.
Q: Is the period of this orbit also 1 year? Q: If not, is it longer or shorter?
It seems clear that a spaceship moving along this smaller orbit should take LESS TIME to complete one cycle. But how much less? Half of a year? One quarter of a year?
Oh, that's right: we can ask Kepler for the answer to this riddle:
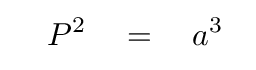
All we need to do is insert the value of a = (1/2) AU into the equation.
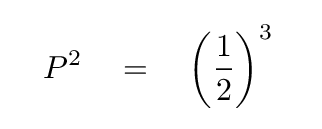
Q: What is the period P of this orbit?
Very good.
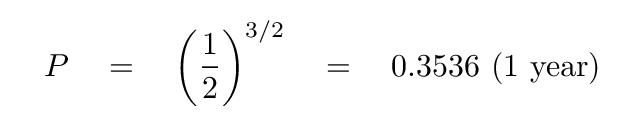
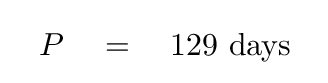
So, a spaceship moving in this circular orbit with a radius of (1/2) AU will take about 129 days to make one complete circle around the Sun.

And so will a ship moving along THIS orbit. It also has the same semi-major axis (but a smaller semi-minor axis).
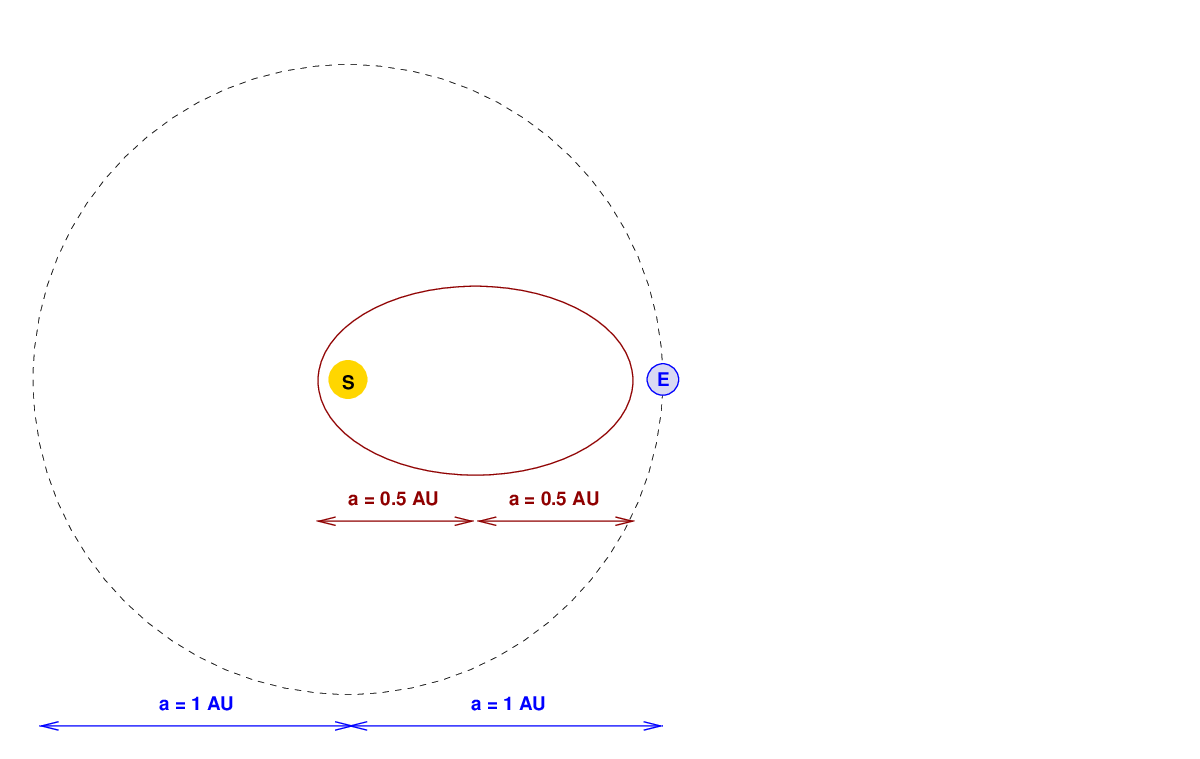
Even this very skinny orbit has a period of about 129 days.
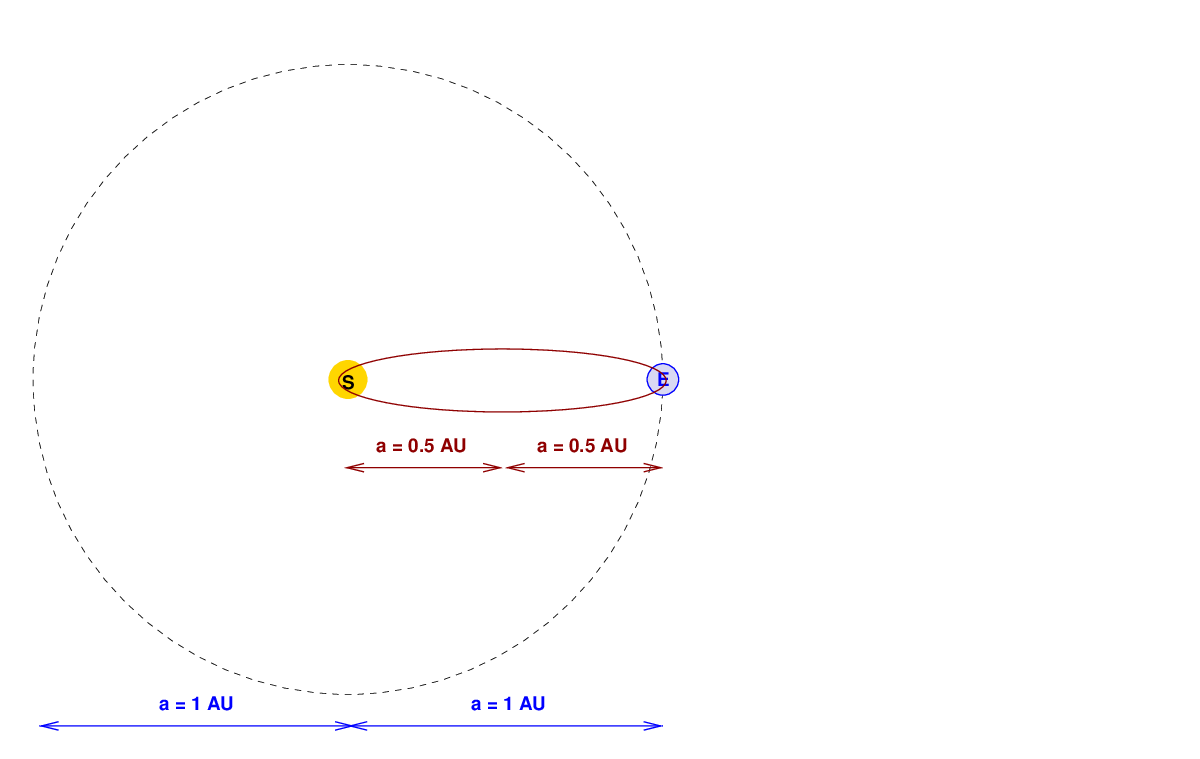
We can take this to extremes. If a ship could somehow survive a trip which passed just above the solar atmosphere, it could complete one very, very, very narrow elliptical orbit in 129 days.
For the final step in solving the puzzle, I will invoke a magic word that strikes fear into the hearts of teachers and professors around the world:
SYMMETRY
Whenever a student claims, "The answer is obvious by symmetry," we have to figure out if she really has discovered a deep, underlying facet of the problem, or if she is simply trying to avoid doing a lot of work. It can be hard to tell sometimes.
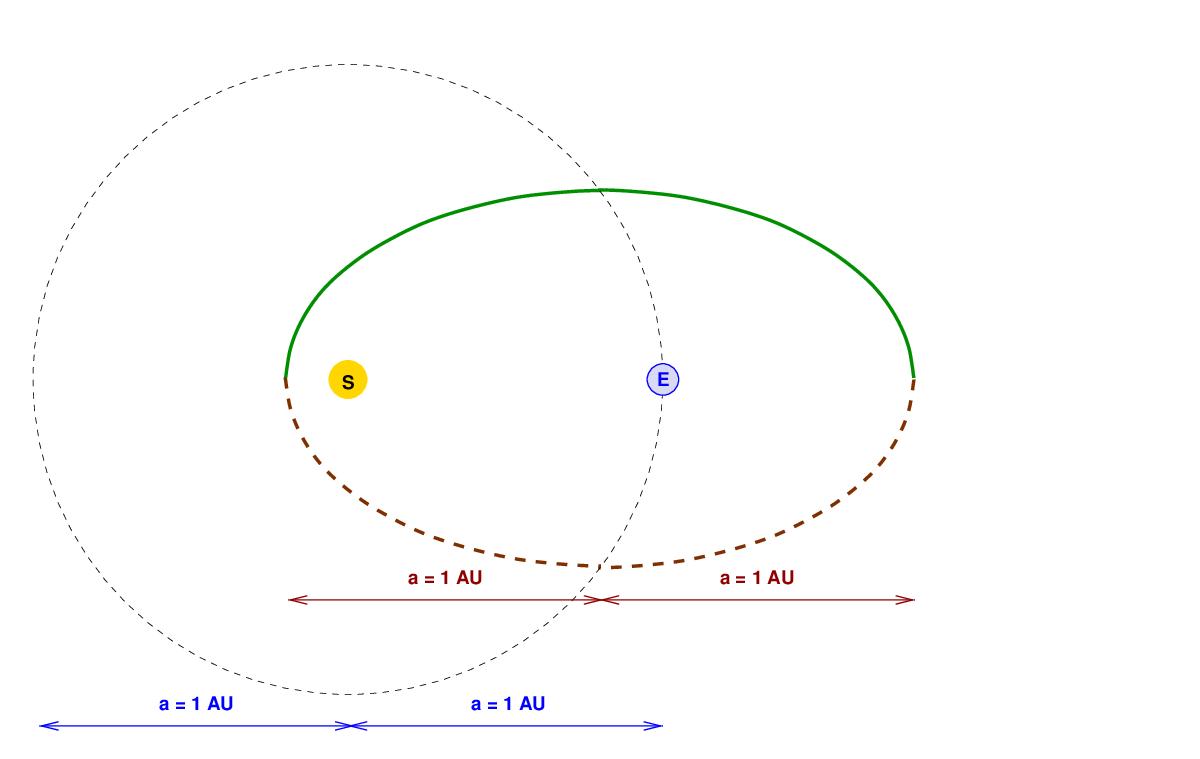
In this case, what I mean by "symmetry" is that ellptical orbits can be split into two equal halves along the the major axis, like this:
It is obvious "by symmetry" that the time required to traverse the top half of the orbit is exactly the same as the time to move along the bottom half of the orbit. Each half requires half of the period. In this case, each half requires 0.5*(365 days) = 182.5 days, approximately.
The same is true of a more eccentric orbit with the same semi-major axis. Motion along both the top and bottom halves will take half the orbital period.
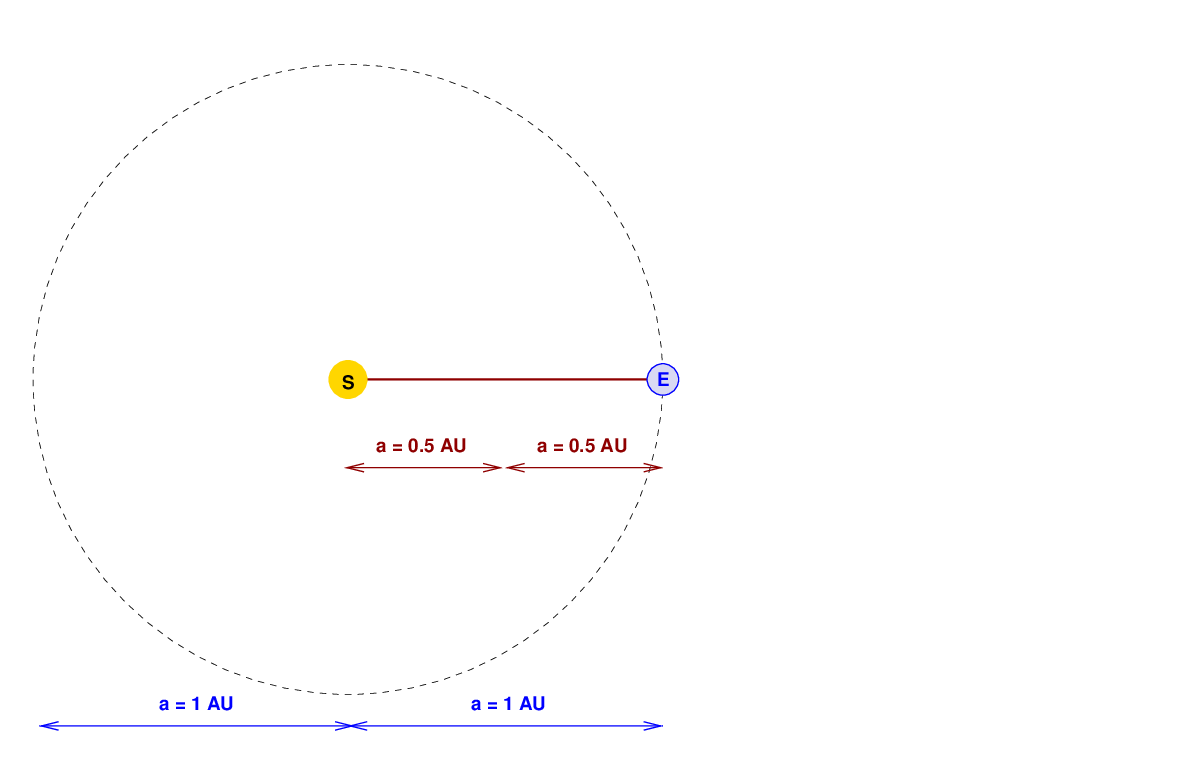
So, let's look again at that very skinny orbit with a semi-major axis of a = 0.5 AU. We know that the round trip -- which consists of motion from the "E" to the "S", and then back from "S" to "E" -- will take 129 days.

Q: How long will it take for an object to move from the "E"
to the "S" in this diagram?