 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
It sounds like a simple question: What body in the Solar System is farthest from the Sun? However, when I try to answer it, I find that one may interpret the question in several ways. In this little presentation, I'll try to describe two such interpretations, and the answer to each. In addition, I'll take a "historical view"; that means I'll try to provide the answer an astronomer would have given in the year 1600, or 1700, or 1800, and so forth. Obviously, as astronomers acquired more powerful instruments -- AND more powerful analytical techniques -- they have been able to find objects farther and farther away from the Sun.
For most of the discussion, I'll avoid the issue of comets, for reasons that I'll explain later. It's not really fair, so there's a short section at the end in which I allow them to be included in the discussion.
One final disclaimer: I am by no means any expert in orbital dynamics, nor am I a member of one of the teams currently searching for new, distant bodies. If I make mistakes, I hope that the real experts will contact me to let me know, so that I can set the story straight.
Table of contents
First, let me restrict the discussion to objects which are definitely bound to the Sun by the force of gravity; in other words, bodies which have closed elliptical orbits, as far as we can tell. This seems a reasonable way to define bodies which are "members of the Solar System." It excludes a relatively small number of objects, mostly comets, with orbits so ill-defined that they (these all mean the same thing)
Second, I'll use as a reference a list maintained by the Minor Planet Center. Specifically, my starting point is the MPCORB file prepared on 2007 June 29. It contains over 338,000 objects.
Right. Now, when I hear the question, What body in the Solar System is farthest from the Sun? I think of two possible ways to answer the question. The difference is one of potential, or maybe patience.
So, let me try to provide answers to each of these possibilities. In each case, I'll track the answer over all of recorded human history; well, what that really means is "over the past 500 years or so," since the answers only start to change after the invention of the telescope and the mathematical work of Kepler and Newton.
Aphelion? What does that mean?
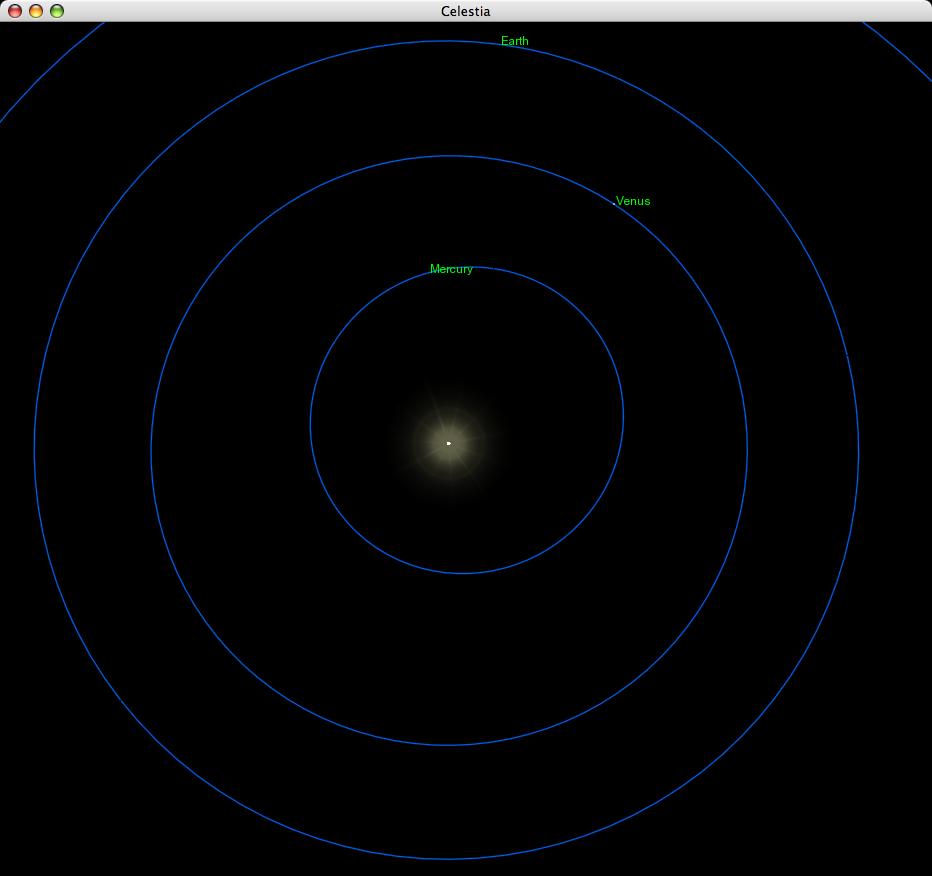
I guess I ought to define a few terms to start. When one object orbits another due to the force of gravity, its orbit must have the shape of a conic section. Closed orbits are, in general, ellipses. Take a look at this picture of the inner Solar System:

The orbits of the Earth and Venus are very nearly circular. Circles are one special sort of ellipse, those in which the eccentricity (abbreviation: "e"), a measure of asymmetry, is exactly zero. Mathematically speaking, a circular orbit can be described as one in which e = 0. The orbit on Mercury, on the other hand, is clearly not a circle; it has e = 0.21. The larger the eccentricity, the longer and skinnier the ellipse. If the eccentricity reaches the critical value of e = 1.0, then the orbit is no longer a closed ellipse, but an open parabola; the body will pass the Sun once, fly off into space, and never return.
Let's look at the orbit of Mercury in more detail.
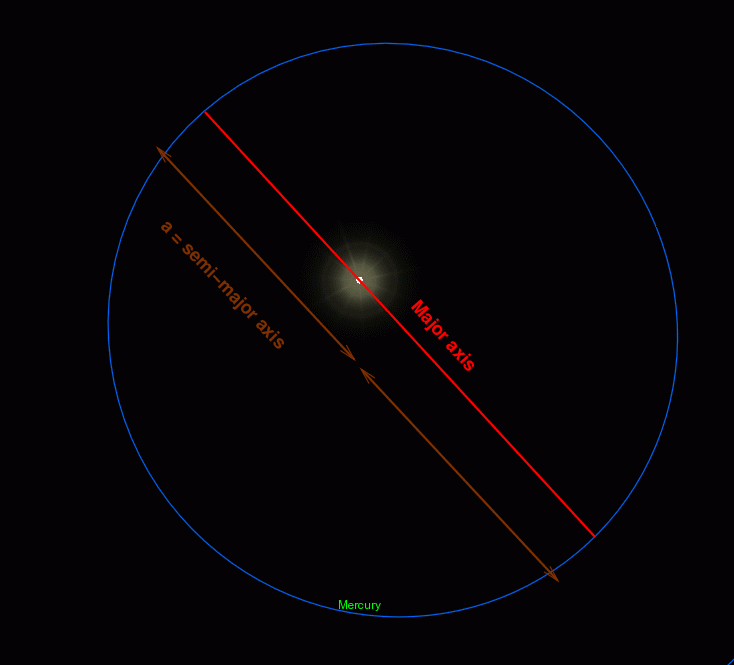
The longest axis of the ellipse is called (not surprisingly) the major axis. It always runs through the Sun, which sits at one of the foci of the ellipse. Half of this longest axis is called the semi-major axis, logically enough. The semi-major axis is one of the quantities used by astronomers to define the shape and orientation of an orbit, and is often denoted by the letter a.
Another way to slice the orbit is to find the positions at which the body is closest to, and farthest from, the Sun. These lie along the major axis, and have special names:

Given the semi-major axis a and eccentricity e of an orbit, one can quickly compute these two distances:
perihelion distance = a * (1 - e)
aphelion distance = a * (1 + e)
Now, if we have a list of bodies and their orbital elements, we can very easily find the one which, at some times in the past and future, attains a distance farther from the Sun than any other body ever does. We simply look for the body in the list which has the largest aphelion distance.
Here are the results, over the past few centuries.
Body with largest known aphelion (excluding comets)
aphelion
Number Name discovered distance (AU) comments
------------------------------------------------------------------
Saturn long ago 10.05
Uranus 1781 20.09 Herschel
Neptune 1846 30.33 predicted!
(134340) Pluto 1930 49.9
(15788) 1993 SB 1993 51.6
(15809) 1994 JS 1994 52.0
1995 DB2 1995.13 52.7
(48639) 1995 TL8 1995.79 64.6
(26181) 1996 GQ21 1996.28 151
1996 PW 1996.58 504 disc at 2.5 AU
(87269) 2000 OO67 2000.58 1083 4 oppositions
2002 RN109 2002.67 1190 80-day arc
2005 VX3 2005.83 2996 81-day arc
------------------------------------------------------------------
Are you puzzled by the strange "names" in the list above? If so, you might want to take a brief break to look at an explanation of minor planet designations.
Perhaps it would help to look at this sequence graphically:
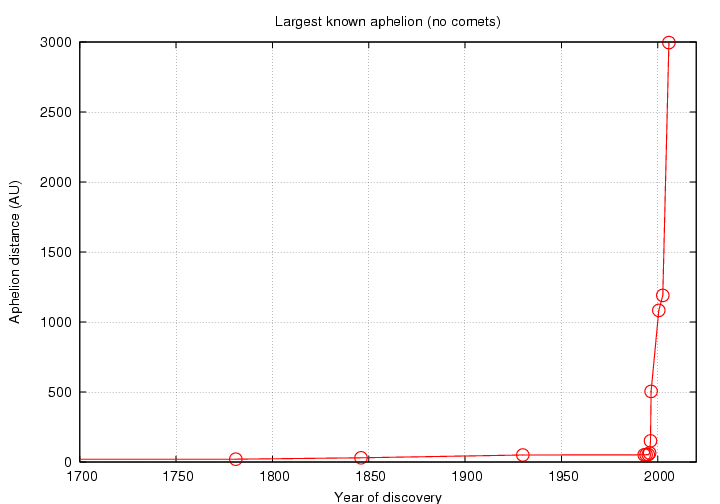
Hmmm. Given the huge range of aphelia, it makes more sense to plot the distances on a logarithmic scale ....
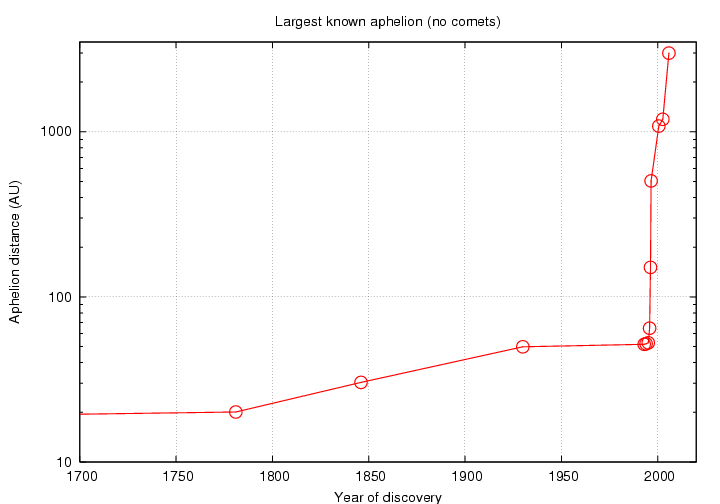
Notes on a few of these objects:
Observer details:
046 Klet. Observers M. Tichy, J. Ticha, Z. Moravec. Measurers M. Tichy,
J. Ticha. 0.57-m f/5.2 reflector + CCD.
104 San Marcello Pistoiese. Observers A. Boattini, L. Tesi. 0.40-m f/5.0
reflector + CCD.
108 Montelupo. Observers M. Tombelli, G. Forti. 0.30-m f/5.7 Schmidt-
Cassegrain + CCD.
122 Pises. Observers C. Cavadore, M. Deldem, B. Gaillard, A. Maury. 0.40-m
reflector + CCD. Long. = 3.5035, rho cos phi' = 0.72017,
rho sin phi' = +0.69176.
353 Nishi Kobe. Observer K. Ito. 0.25-m f/6.3 Schmidt-Cassegrain + CCD.
360 Kuma Kogen. Observer A. Nakamura. 0.60-m f/6.0 Ritchey-Chretien + CCD.
367 Yatsuka. Observer H. Abe. 0.26-m f/6.0 reflector + CCD.
388 Tokyo-Mitaka. Observers N. Yamamoto, D. Kinoshita, T. Saito, A. Obara.
Measurer I. Sato. 0.50-m reflector + CCD.
422 Loomberah. Observer G. J. Garradd. 0.25-m f/4.1 reflector + CCD.
540 Linz. Observers E. Kolmhofer, H. Raab. 0.3-m f/5.2 Schmidt-Cassegrain
+ CCD.
557 Ondrejov. Observer P. Pravec. 0.65-m f/3.6 reflector + CCD.
566 Haleakala-NEAT/GEODSS. Observers E. F. Helin, S. Pravdo, K. J. Lawrence
for the NEAT team. 1.0-m f/2.2 GEODSS telescope + CCD.
587 Sormano. Observers P. Sicoli, V. Giuliani, P. Chiavenna. 0.5-m reflector
+ CCD.
608 Haleakala-AMOS. Observers A. Alday, K. Moore, M. Tranilla, T. Goggia,
A. Sylva. Measurers G. Fricke, K. Imada, J. Africano, P. Sydney,
D. Nishimoto, D. O'Connell, P. Kervin, B. Kraszewski, V. Soo Hoo. 1.2-m
reflector + CCD.
673 Table Mountain Observatory, Wrightwood. Observer D. L. Rabinowitz.
0.6-m reflector + CCD.
817 Sudbury. Observer D. di Cicco. 0.41-m Schmidt-Cassegrain + CCD.
867 Saji. Observers M. Yamanishi, A. Miyamoto, M. Aimoto, T. Oribe. 1.03-m
f/4.2 reflector + CCD.
900 Moriyama. Observer Y. Ikari. 0.25-m f/6.3 reflector + CCD.
Dave Herald provides a nice illustration. He writes that when he computes an orbit for 2002 RN109 using Find_Orb, he finds an aphelion distance of 2085 AU -- very different from the 1190 AU based on the parameters in the MPCORB file. It's clear that we have only very rough notions of the shape and size of these record-holding bodies.
This is how impatient people might interpret the original question. Based on what we know, right now, which object is at this very instant the most distant from the Sun?
In order to answer it, we need the same compilation of information on the orbital parameters of all known bodies in the Solar System; but we also need a new tool. We can't simply plug a couple of numbers into a simple equation this time, as we did to determine the aphelion distance of each object. Instead, we need to apply rather sophisticated mathematical calculations over and over and OVER again to work out the position of each object at some particular time. I grabbed some code from a project called libnova to do this work for me. I know that the real professionals in this business have their own code; I suspect that many of them have written it themselves.
Given both a big list of objects and software to compute positions, I did the following:
Why start in 1990? It was at about that time that astronomers started searching in earnest for faint trans-neptunian objects (TNOs). Before that time, the most distant object was simply the most distant known planet.
So, here's what I found.
The current most distant object known
Number Name when distance (AU) comments
------------------------------------------------------------------
Saturn long ago 10.1
Uranus 1781 19.0 at discovery
Neptune 1846 30.0 at discovery
(134340) Pluto 1930 41.3 inbound ...
Neptune 1979.11 30.3 (Feb 9, 1979)
(15760) 1992 QB1 1992.67 40.9
1993 FW 1993.25 42.2
1994 ES2 1994.25 45.9
1995 WY2 1995.92 47.8
1999 CD158 1999.09 48.5
1999 KR18 1999.42 52.5
2000 AF255 2000.00 53.4 inbound ...
(148209) 2000 CR105 2001.09 53.2
2003 QX113 2003.67 58.4
(136199) Eris 2003.84 97.0 aka 2003 UB313
------------------------------------------------------------------
Here's the same information in a graph:
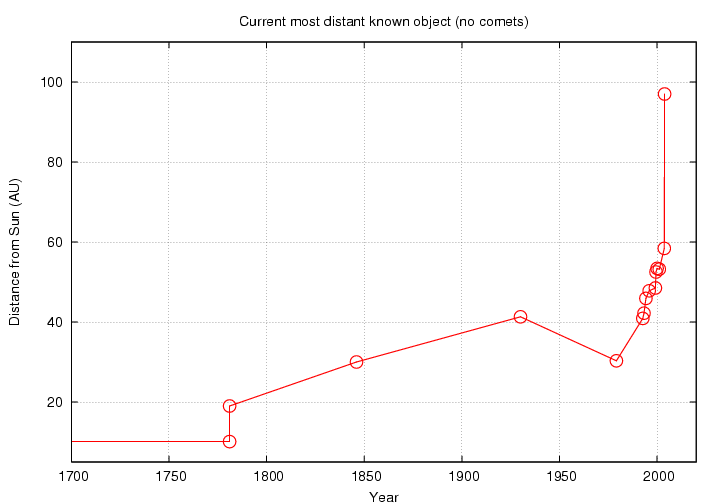
Note that during the intervals 1930-1979 and 2000-2001, the most distant known object (Pluto and 2000 AF255, respectively) was on the inbound section of its orbit; thus, in some sense, the size of the "known Solar System" was gradually shrinking. And, in fact, it is happening right now: (136199) Eris was 97.0 AU from the Sun when discovered, but is only 96.8 AU from the Sun now, in July 2007.
I've excluded comets from the discussions so far -- why? There are two main reasons:

The jets act like very weak rocket engines, pushing the comet slightly and altering its orbit. Due to these "non-gravitational forces", the orbits of comets can change significantly from one passage through the inner Solar System to the next.
Comet C/1853 E1 (Secchi) is one of a large number of comets with parabolic orbits. Given that there are sufficient observations of the comet, 91 in right ascension and the same number in declination, it proves possible to calculate a better orbit. Comet Secchi's orbit is hyperbolic, the most hyperbolic of any comet except C/1980 E1 (Bowell). Comet Secchi is in no way associated with Comet C/1664 W1.
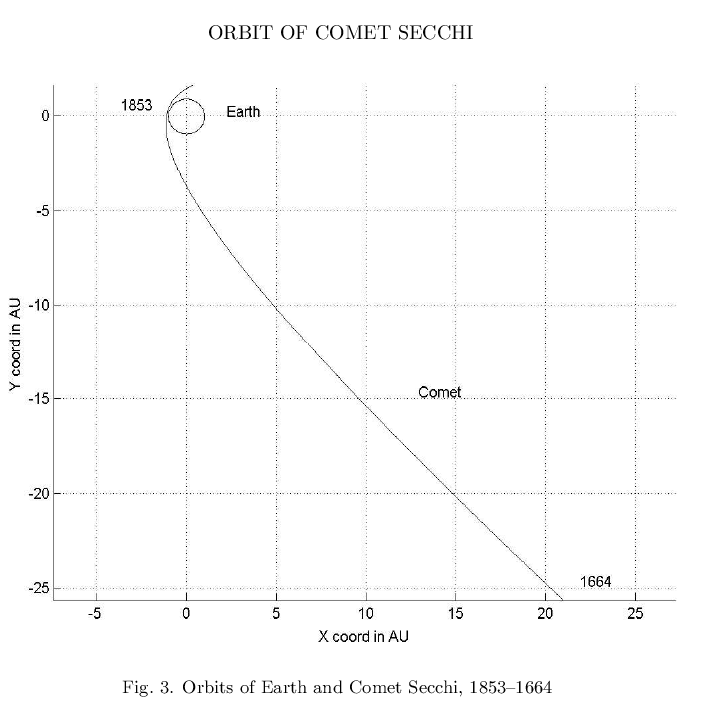
If a comet isn't bound to the Sun -- if it will fly off into space and never return -- does it really count as a member of the Solar System? I'm not sure ...
However, suppose that we put these issues aside, and allow comets to enter to our discussion. We can again ask the two questions:
Let's see what the answers are ... I grabbed orbital elements for comets from one of the sub-pages under the main MPC site; specifically, those listed as Observable Comets. I'm sure that this is only a subset of all known cometary orbits, but it's the best I could find.
If we discard any comets with eccentricities greater than or equal to 1, which of the remaining bodies has the largest aphelion distance? The list of objects derived from my subsample is very short; I'm sure that there are many historical comets which would appear after Halley, if only I could find their orbital elements ...
Comet with largest known aphelion (and closed orbit)
aphelion
Desig Name discovered* distance (AU) comments
------------------------------------------------------------------
1P Halley 1705 35.1 date of orbit calc
C/1995_O1 Hale-Bopp 1995 369
C/2001_HT50 LINEAR-NEAT 2001 2507
C/2002_L9 NEAT 2002 14245
------------------------------------------------------------------
The names of the final two comets on the list may need a bit of explanation. LINEAR refers to the LIncoln Near-Earth Asteroid Research program, a collaboration between the Air Force and MIT's Lincoln Laboratories. NEAT is the Near-Earth Asteroid Tracking program, run by JPL, with telescopes in Hawaii and on Mount Palomar. These two programs are among the most productive search programs running.
The last entry in this list seems pretty darn large. Can we really trust the number in the table? I suspect not. If we go to the MPC web site with the orbital elements for this comet, we are shown two sets of elements:
The following orbital elements are taken from MPC 52905: C/2002 L9 (NEAT) Epoch 2004 Apr. 25.0 TT = JDT 2453120.5 T 2004 Apr. 6.0527 TT MPC q 7.033035 (2000.0) P Q z +0.000214 Peri. 231.4315 +0.4870305 -0.0586674 +/-0.000003 Node 110.4573 -0.1545612 +0.9762041 e 0.998498 Incl. 68.4456 -0.8596000 -0.2087670 From 142 observations 2002 June 6-2004 Oct. 10, mean residual 0".6. Elements are also available for the current standard epoch: C/2002 L9 (NEAT) Epoch 2007 Apr. 10.0 TT = JDT 2454200.5 T 2004 Apr. 6.2319 TT MPC q 7.033192 (2000.0) P Q z +0.000140 Peri. 231.4541 +0.4865298 -0.0580439 +/-0.000003 Node 110.4001 -0.1546207 +0.9763194 e 0.999013 Incl. 68.4451 -0.8598728 -0.2084021
The good news is that there are measurements of this object over quite a long span of time: over two years. The bad news is that even very small changes in the eccentricity lead to large differences in the aphelion distance. For example,
Epoch 2004 Apr. 25.0 orbit has a = 4682 AU
e = 0.998498
---> aphelion = 9358 AU
Epoch 2007 Apr. 10.0 orbit has a = 7126 AU
e = 0.999013
---> aphelion = 14245 AU
I'd conclude that we don't know that aphelion distance of this comet (or, probably, others like it) very well at all; but we can say that it goes very, very, VERY far away from the Sun.
Finally, let's try to use the orbital elements of comets with elliptical orbits to make a list of the known comet which is farthest from the Sun right NOW, over the past few centuries. It's an even shorter list -- again, with the caveat that it is based on a subset of all known cometary orbits.
Comet (with elliptical orbit) farthest from the Sun right NOW
aphelion
Desig Name discovered* distance (AU) comments
------------------------------------------------------------------------
1P Halley 1705 30.8 distance July 2007
------------------------------------------------------------------------
This shouldn't really be too surprising, in a way. We (usually) discover comets when they zip through the inner Solar System, since they are both closer to the Earth at that time and intrinsically luminous due to their long tails and bright comae. I included only comets with well-measured orbits in my calculations ... and that means, for the most part, comets which have been observed on more than one perihelion passage ... which in turn means, for the most part, periodic comets. So the winner of this contest will typically be the periodic comet with the largest orbit; and that means 1P/Halley.
Halley's comet has a semi-major axis of 17.8 AU, which is still the largest of any periodic comet in the dataset I could find. There are only three other periodic comets with semi-major axes greater than 10 AU, and each of them has been discovered near perihelion in the past ten years; that means that they are all currently near the inner portions of their orbits, closer to the Sun right NOW than 1P/Halley.
After doing all this work, I wanted to have a little fun. Suppose that we decide upon this rather silly definition for "The Size of the Solar System:"
The Size of the Solar System is the distance between the Sun and the most distant known body which is gravitationally bound to the Sun.
It doesn't make much sense, really, but allow it for the sake of argument. For millenia, then, the Solar System was bounded by the planet Saturn, about 10 AU from the Sun. But things started to change after the invention of the telescope and the work of Kepler and Newton. Let's look at how the Solar System -- according to this definition -- changed over the next 400 years ...
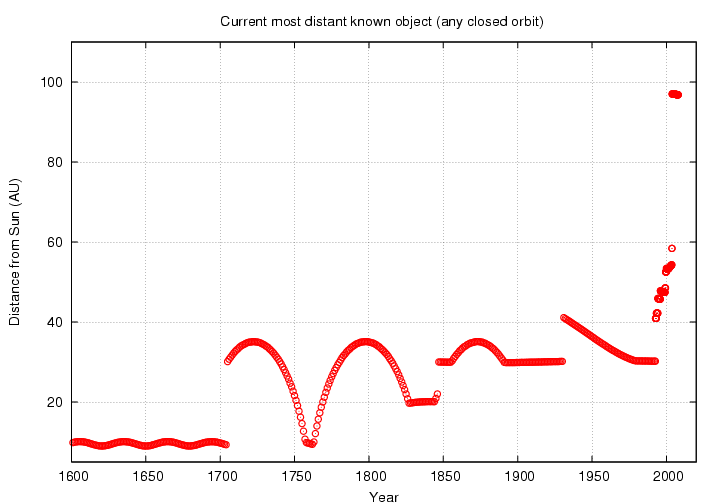
Can you figure out what's happening in this figure? If not, you might glance at an annotated version of the figure.
Some of the names you've seen in this document are pretty strange: "1996 PW", for example, or "(26181) 1996 GQ21". What do they mean? Why aren't they sort and sweet, like "Saturn" or "Pluto"?
The problem is that lots of objects are discovered each year -- so many that's it is difficult to keep track of them all. Moreover, an object observed tonight might turn out to be the same body measured on another night several years ago ... or it might not. It would be a disaster to give two different names to the same object, or the same name to two different objects. In order to maintain some sense of order, the Minor Planet Center has devised a four-step procedure for giving designations, and eventually "names", to objects within the Solar System.
On the other hand, if the MPC finds several measurements which do not match the orbits of any known object, but which are consistent with a reasonable orbit within the Solar System, it decrees that a new object has been found, and creates for it a provisional designation. These are in the form of a code which describes roughly the date on which the measurements were "linked" into a new orbit. You can read the official rules if you like, but the basic idea is
2006 TC12 = 2006 T C12
| | |----- index within half-month
| |
| --------- code for half-month
|
|------------ year
The half-months of the year run from "A" (first half of Jan) to "Y" (second half of Dec), skipping the letter "I". The first object discovered within a half-month is "A", the second "B", up to "Z" for the twenty-fifth (again, "I" is unused). If more than 25 have been found, the index starts accumulating multipliers: "A1", "B1", and so forth. The multipliers are supposed to be written as subscripts, but I have not done so in the tables in this document (to make it easier for others to use those tables).
Can you figure out when the object above was discovered? How many other objects preceded it within its half-month? (The answers)
Astronomers often place the number of an asteroid within parantheses in their writings. Thus, they might refer to (1) Ceres or (15788) 1993 SB.
In practice, things can get messy, as some people believe that names are very important. Just who is the official discover(s)? What names are acceptable? What happens if someone attempts to give an object a name without going through the official channels? I don't want to go into any detail; interested readers can find examples in the recent past.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.