Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In late 2013, the comet ISON (comet C/2012 S1) will pass through the inner solar system, zipping past the Sun in late November and then flying out again past the Earth in December.
Click on the image to start animation
It will be closest to the Earth around Dec 25, 2013, at a distance of roughly 0.43 AU. It will appear brightest about one month earlier, in late November and early December.
But how bright will it be? Will it turn out to look like Comet Hale-Bopp,
Image courtesy of
Drew Sorenson and the Ames Astronomers
or more like Comet C/2011 L4 PanSTARRS?
Image taken Mar 14, 2013, around 8 PM, 10 sec at f/16
Well, it's a risky business to predict the behavior of comets, especially new ones which are making their first pass through the inner solar system. Some people just can't resist, though, and they will need all the observations they can get in order to improve their predictions. So, how can we help?
Contents
Photometry is a fancy word for "measurement of light". The goal here is to determine the apparent magnitude of a comet by comparing its brightness to that of a star (or stars) of known brightness. Let's begin with a simple example, involving just stars; we'll leave comets for later.
The first step is to acquire an image of some stars of interest. Below is a CCD image taken through a V filter with the RIT Observatory's 12-inch telescope.
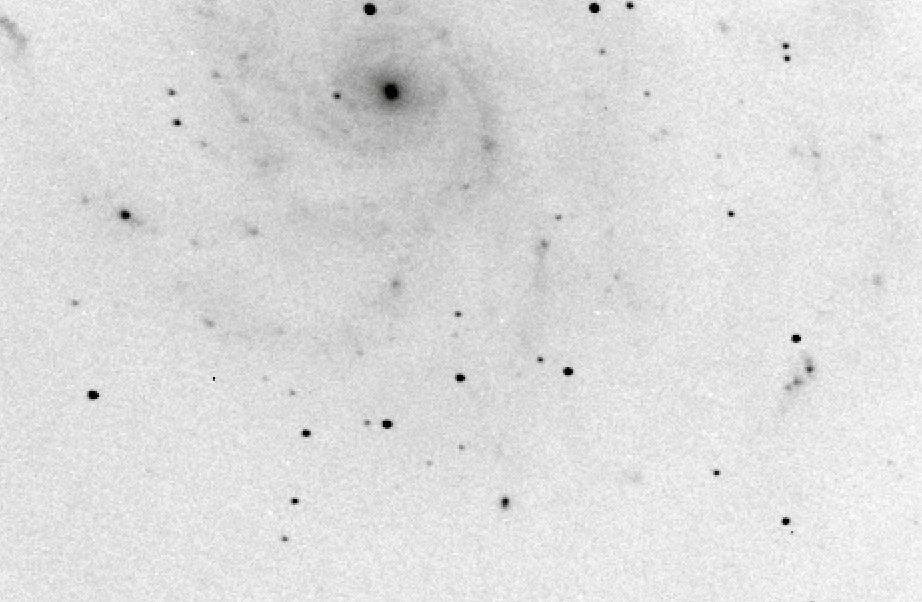
Do you recognize this field?
Hint: there's a spiral galaxy in the background
Hint: one of the stars is a supernova
Yes, that's right: it's the spiral galaxy M101, and the supernova is SN 2011fe!
Suppose we want to measure the magnitude of the supernova: we'll call it our "target". We must do three things:
There are a number of ways to measure the brightness of objects in a digital image. You can look at the pixel values of each object directly, or semi-directly in a radial profile, as shown below.
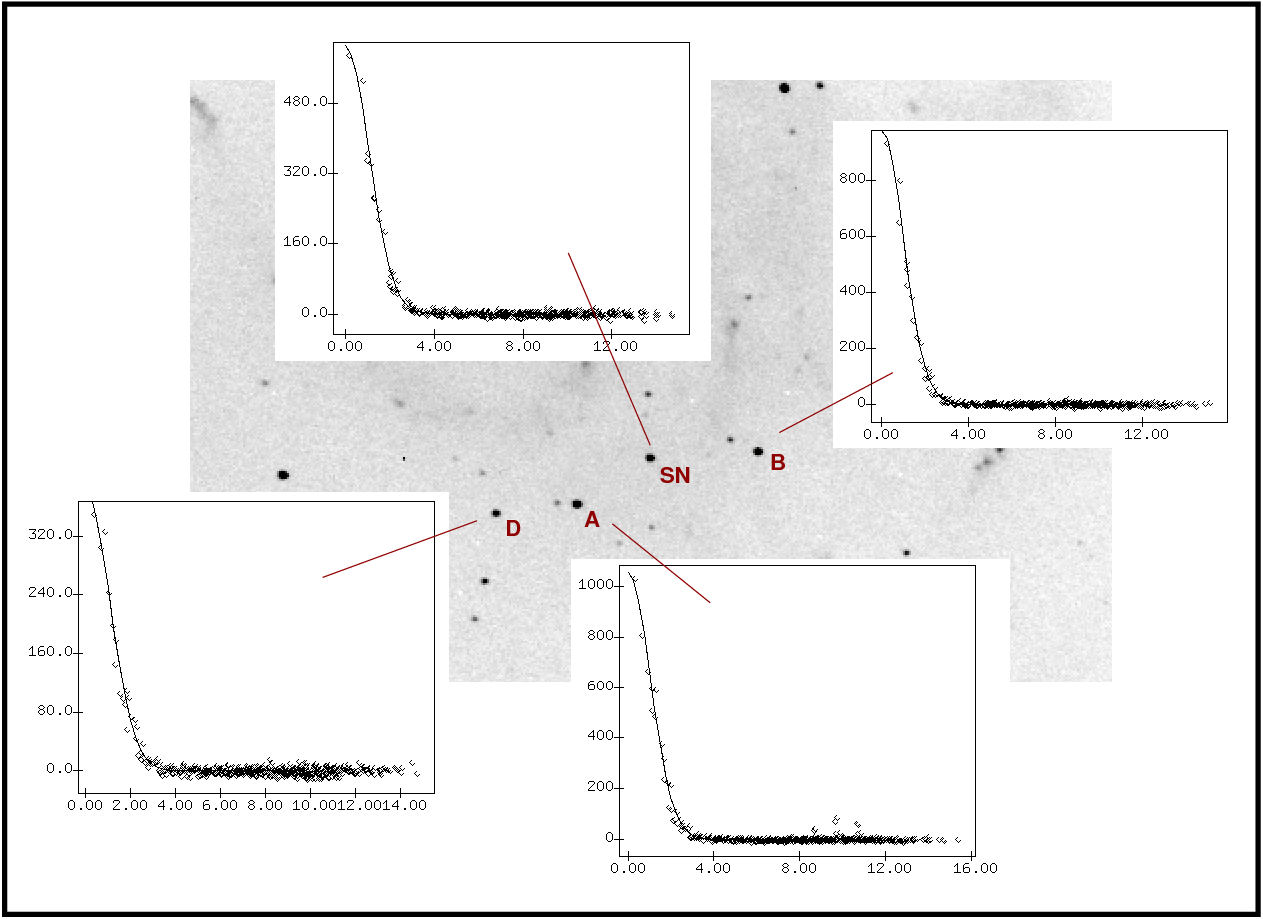
Use the figure above to estimate the peak pixel value for each star:
------------------------------
A peak =
B peak =
D peak =
SN peak =
------------------------------
Q: What is the the brightness of the SN, relative to star A,
measured in this manner?
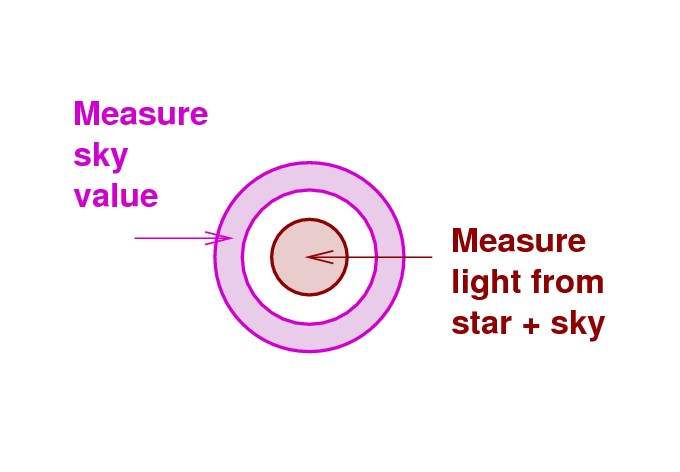
Another way to measure the brightness of stars in a digital image is to add up the values from all the pixels which fall inside a circular aperture around each star. In order to separate light from the star from the light from the background sky, we need to define a small circular aperture (for measuring light from the star PLUS the sky underneath it) and an annulus around it (for measuring light from the sky alone):
We then place this aperture over our target, and measure the light falling with in the central aperture and the average value in the annulus ...
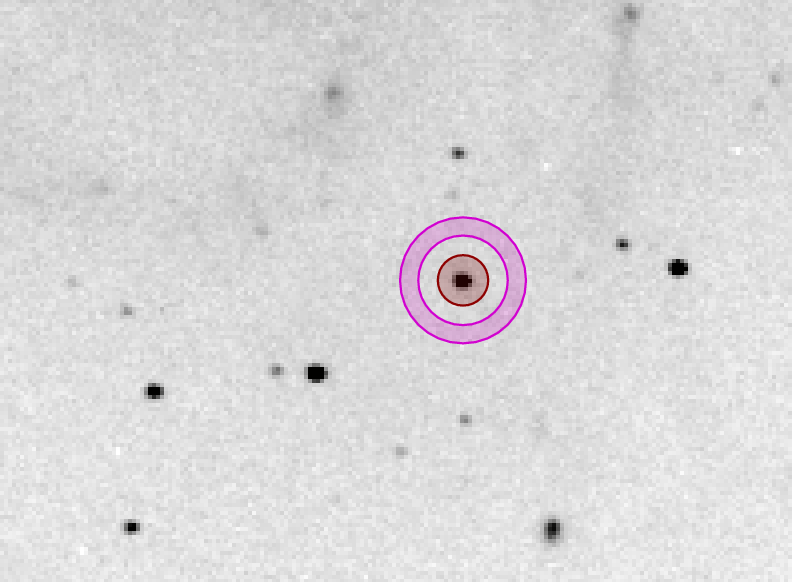
.... then repeat for each comparison star.
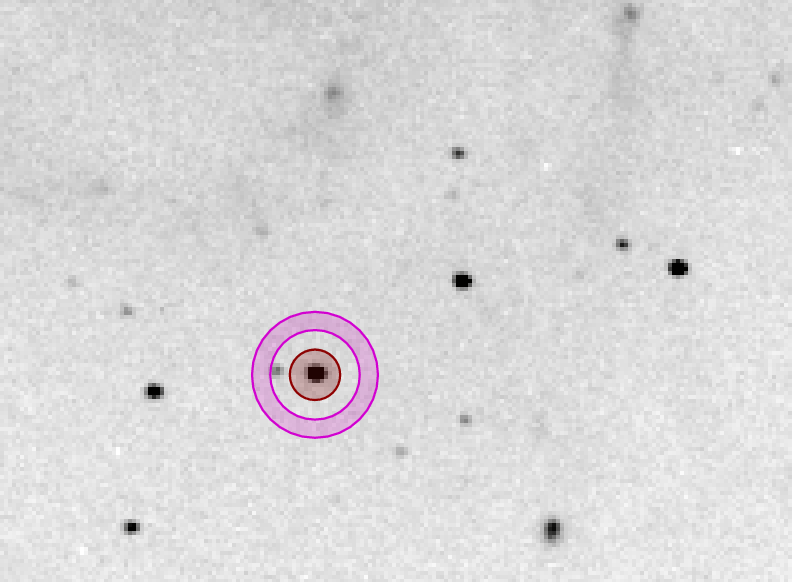
In this particular image, I measured the following values. Can you subtract the sky's contribution from the counts inside the aperture, and fill in the final column of the table?
star counts in aperture pixels in sky value counts from
(star + sky) aperture star only
-----------------------------------------------------------------------------
SN 5665 112 10
A 8319 112 8
B 7061 112 5
D 3417 112 4
-----------------------------------------------------------------------------
Q: What is the the brightness of the SN, relative to star A,
measured in this manner?
Q: How does this compare to the value determined from the
radial profiles earlier?
There are many ways to find the magnitudes of comparison stars. You could use a planetarium program. I like the Aladin tool from the CDS .
It allows you to access a picture of any region of the sky from a wide range of digitized surveys,
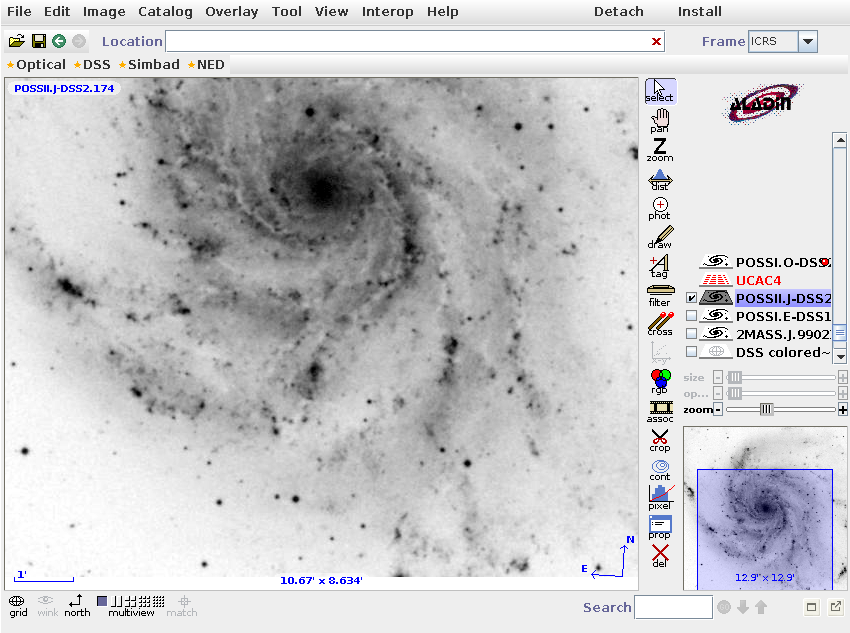
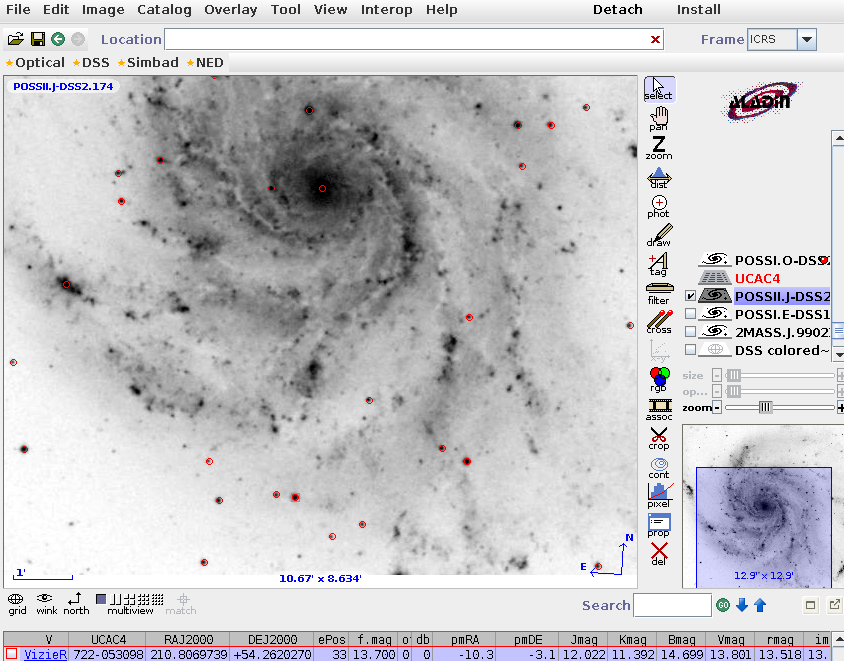
and then place an overlay on the picture, with links to hundreds of catalogs.
If you know the intensity I of each object, and the magnitude m of a comparison star, then it's easy to compute the magnitude of the target:
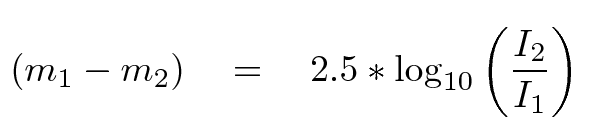
Yes, yes, this is ignoring a number of factors, including the possiblity that the color of the comet is not the same as the color of the comparison star. If you want more details, you can read a few of them in this lecture; but for the full story, you ought to read a good book.
The basic techniques of photometry work just fine when one is comparing stars to other stars, because the light from all stars has the same shape and size.
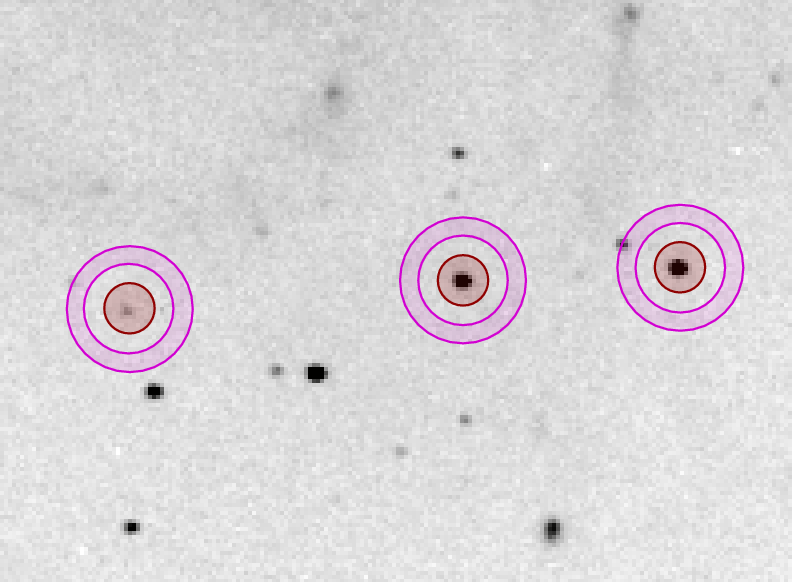
If a comet is so far from Earth that it appears nearly stellar, then we might still be able to use simple aperture photometry to measure the light from the comet. What do you think of this image of Comet ISON taken on Feb 23, 2013, with the WIYN 0.9-meter telescope?
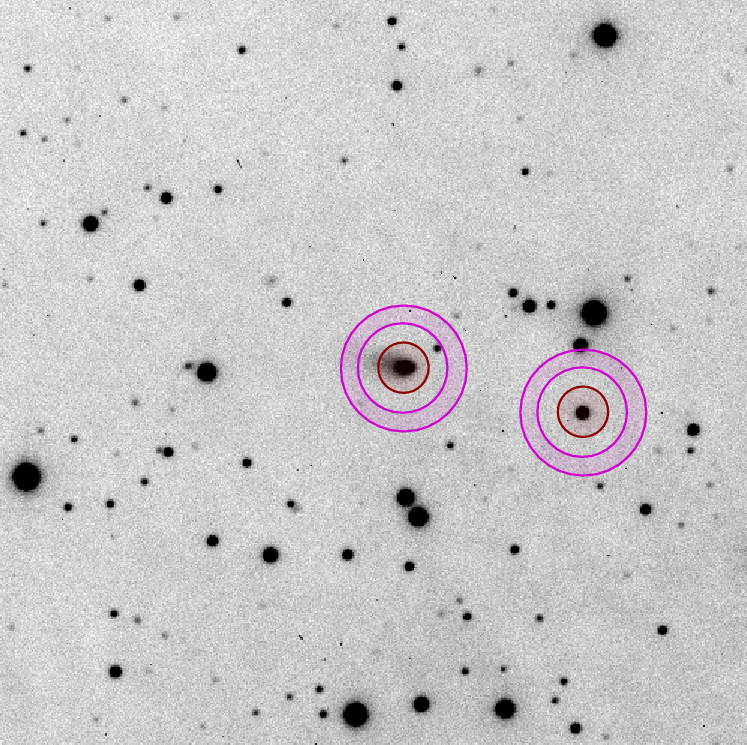
When a comet approaches the Earth, its light may appear spread out over a large area. How can we now compare the light from the comet to that from a comparison star?
Image of Comet Hyakutake
copyright
Rick Scott
and
Joe Orman
Well, there's no easy answer. Observers who measure magnitudes visually (with their eyes) often try to defocus their binoculars or telescopes until starlight is spread out over an area similar to that of the comet; they can then fairly compare the brightness of the comet to that of the stars.
Can you do this with CCDs, too? Give it a try and find out!
The wierd "absolute magnitudes" of comets
There's one final point concerning the measurement of comets (and asteroids, and other bodies in the solar system) which may confuse you -- it certainly confuses me.
When we talk about the magnitudes of stars, we normally distinguish two varieties:
What's the difference? Well, take a look at the constellation of Canis Major:
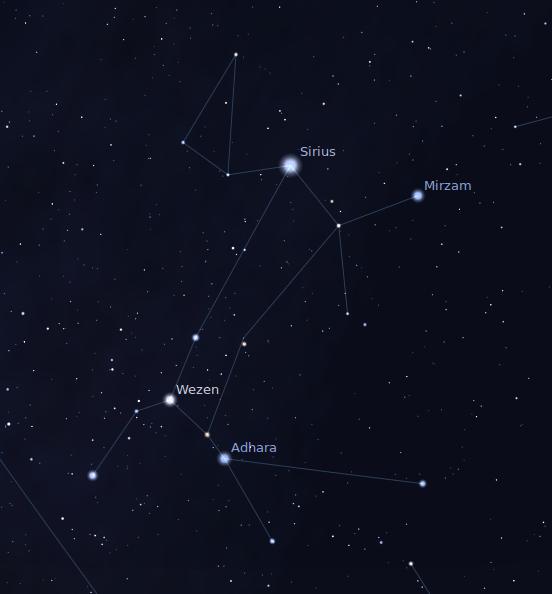
You all know that Sirius is the brightest star in the sky, right? That is, it appears brighter to human eyes than any other star. The star called Mirzam, at the end of one of the doggy's forepaws, is not nearly as bright. The apparent magnitudes of these stars are:
But this is not really a fair comparison of the stars. Why not? Because Sirus is one of the closest stars to the Sun ...
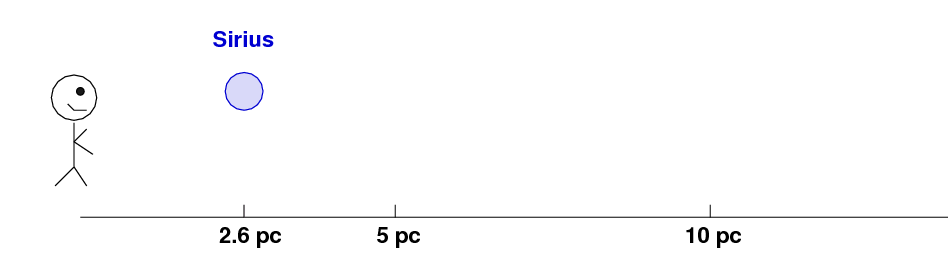
... but Marzam is much farther away.
In order to compare these stars' luminosities fairly, we need to observe them at the same distance from us. Suppose that, with the help of some friendly aliens, we could move both stars to the standard distance of 10 parsecs from the Sun.
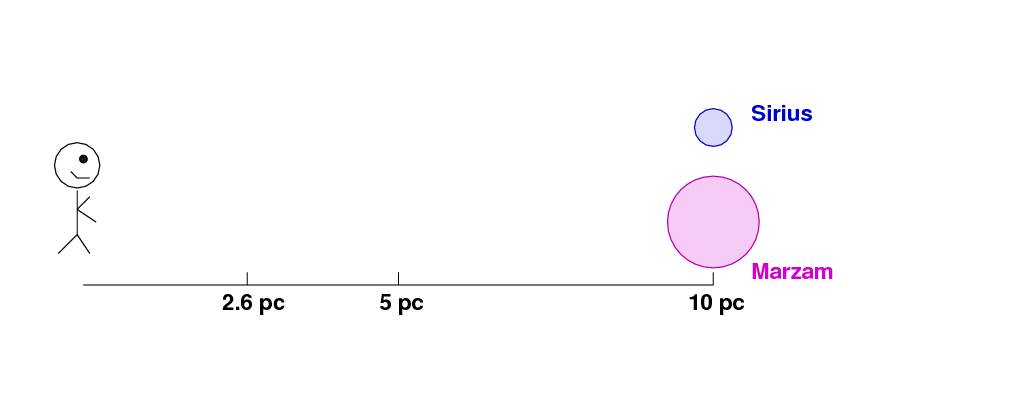
We define the absolute magnitude of a star to be the magnitude it would have if observed from this standard distance. In this particular case, Sirius would be moved farther away, and so fade, while Marzam would grow much brighter.
The notion of absolute magnitude is to level the playing field: by putting all the stars at the same distance, their relative apparent brightness really does reflect their relative luminosity: powerful stars will now look brighter than feeble ones.
Okay, that was the story for stars. It turns out that one can do something similar for objects within our Solar System: to remove the effects that different distances can have on the apparent brightness of objects. In the solar system, though, it's a bit more complicated because comets and asteroids shine by reflected light, not by producing their own energy.
Consider the effect of distance from the observer alone. Asteroids A and B are identical: same size, same shape, same surface properties.
Q: Which asteroid will appear brighter to the
observer on Earth?
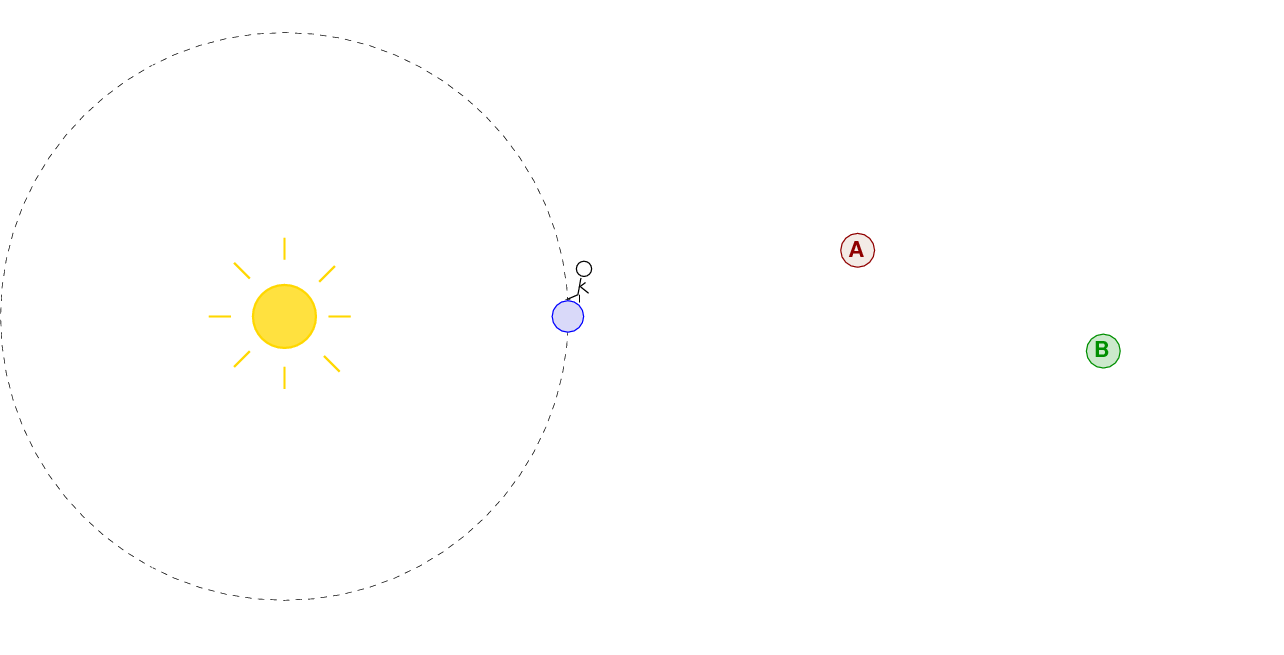
Okay, we can fix that difference by placing both objects at the same distance from the observer, right?
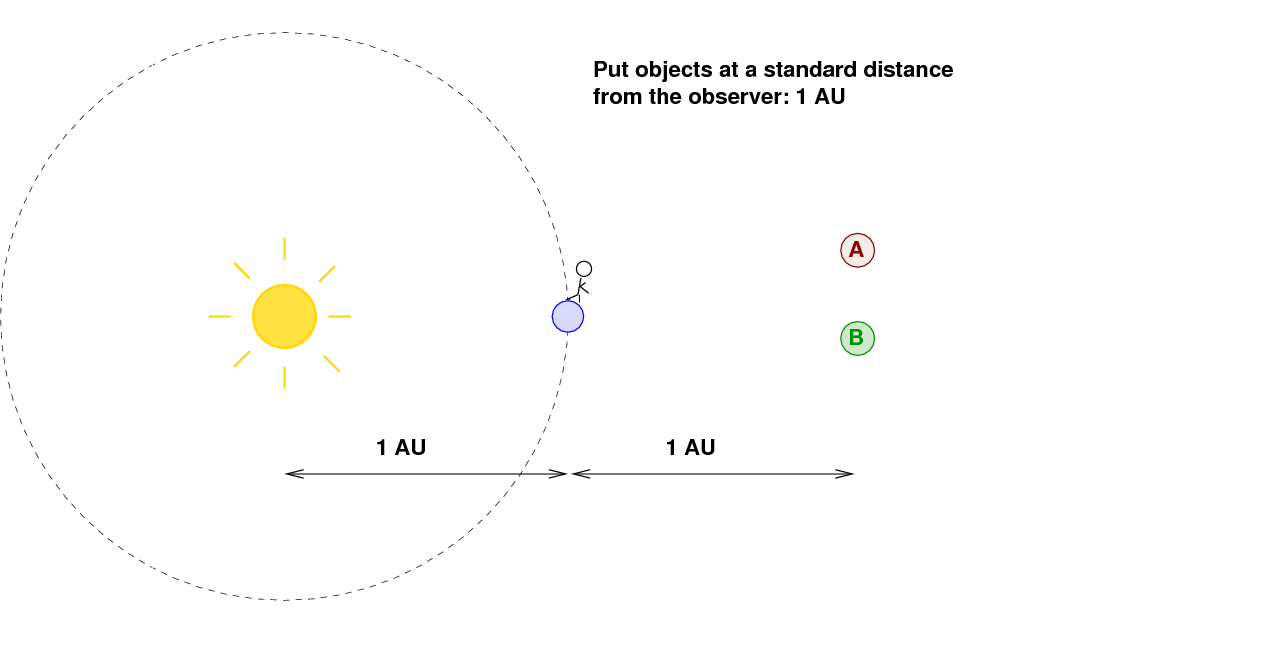
But suppose that we imagine two astronomers: one on Earth, looking at an asteroid exactly 1 AU from him, and an observer on Saturn, who is looking at an asteroid exactly 1 AU away from HIM.
Q: Will asteroid A, seen from Earth, have the
apparent brightness as asteroid B, seen from Saturn?
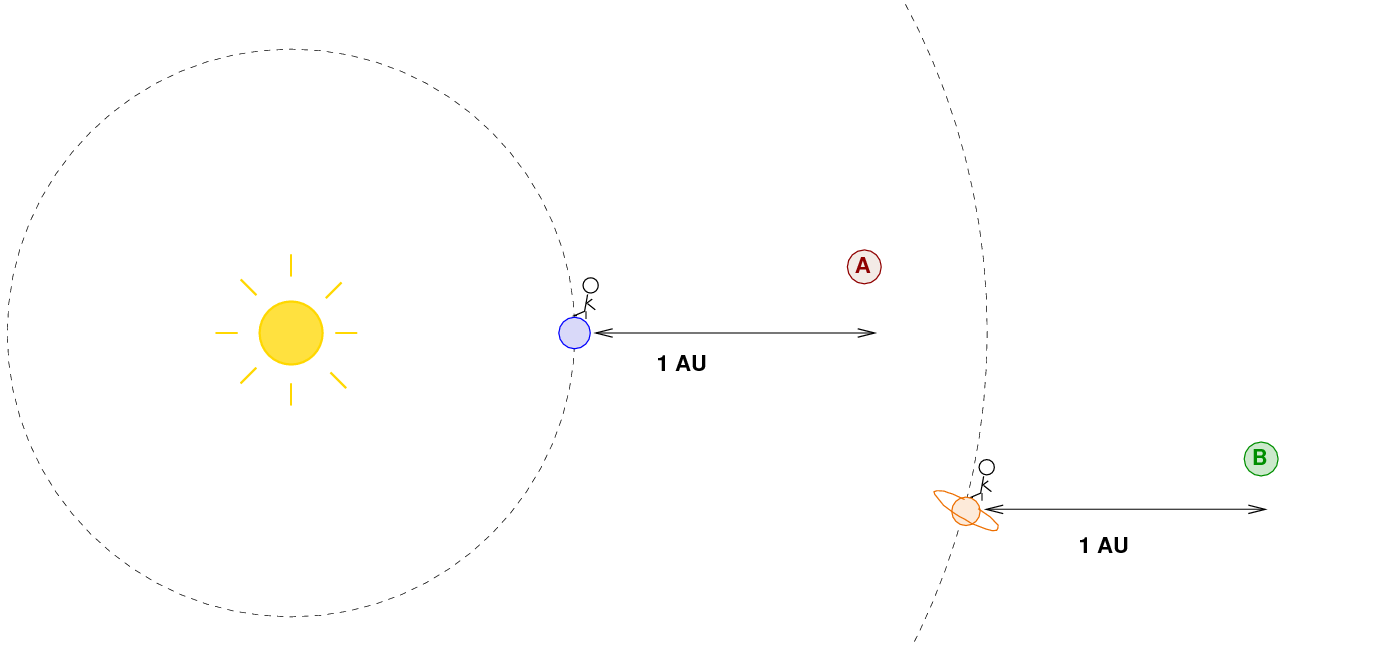
No, of course not: the intensity of sunlight at the distance of Saturn is much lower than the intensity at the distance of the Earth. That means that the light striking asteroid B will be weaker than that striking asteroid A; and, therefore, asteroid B will appear fainter to the astronomer on Saturn than asteroid A appears to the astronomer on Earth.
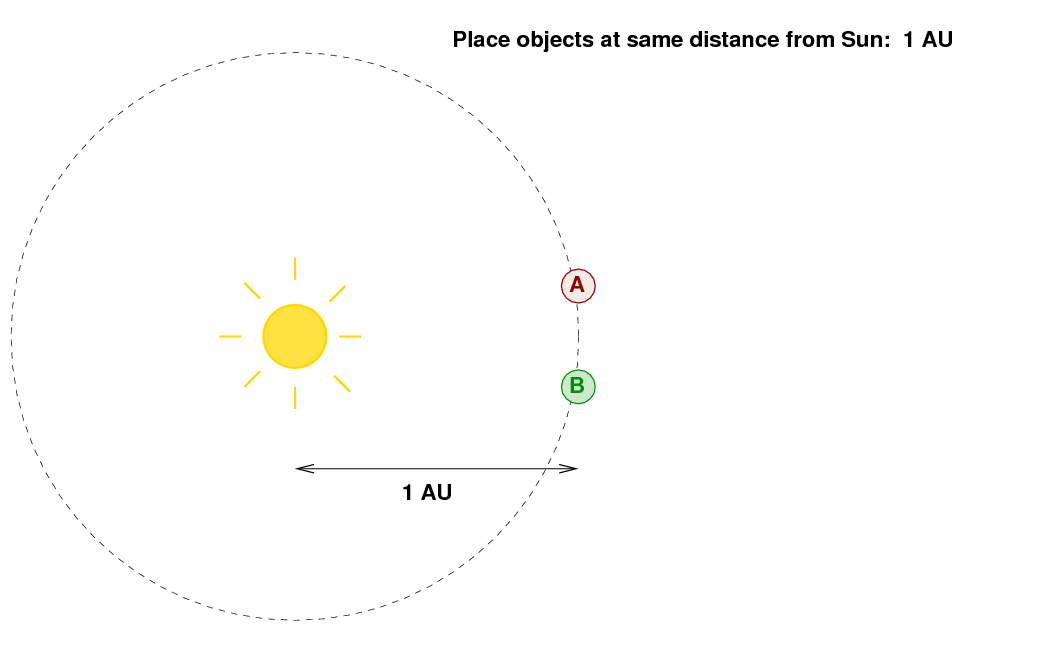
In order to make a fair comparison between all asteroids and comets and moons in the Solar System, astronomers have come up with a standard procedure:
Step 1: place the object at a distance of 1 AU from the Sun.
Step 2: place the observer at a distance of 1 AU from the object.
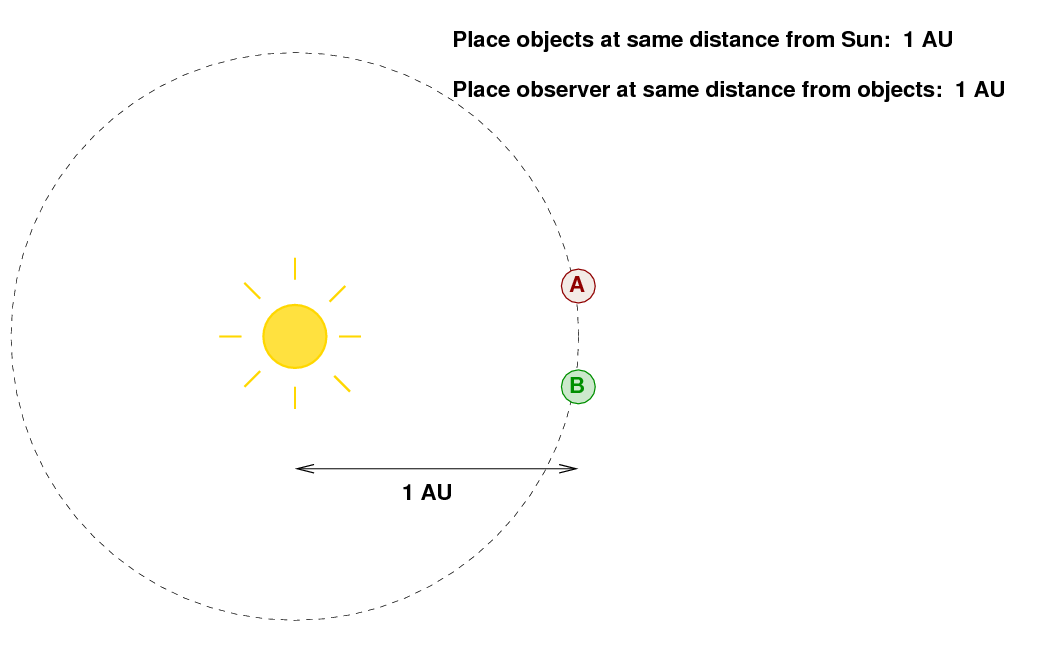
Ouch.
If one could somehow arrange for the observer to survive, the measurements he made would be called absolute magnitudes, denoted with the letter H.
There are additional complications, dealing with the angle between the Sun, the object, and the observer. See the references below for more information on the subject.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.