Astronomers often take a series of images of the same field of stars when studying a variable star. What is the best way to measure the change in brightness of the variable object? The simplest method is to compare the brightness of the variable to that of a single reference star. However, if that reference star turns out to be variable itself, then its changes in brightness will contaminate the measurements of the target star. It would be better to use a number of stars in the field as references; the more stars, the better. In many cases, images taken at different times are not perfectly aligned, causing some stars to fall off the edges and appear only in a subset of the entire dataset. Is there any way to include all these stars in the analysis, even those which do not appear in all images?
Yes. The technique called inhomogeneous ensemble photometry uses a large set of stars (the "ensemble") to create a photometric reference level. It includes as many measurements as possible, even those from stars which don't appear in all frames (hence "inhomogenous"). A very good reference for this technique is
I have written software to implement this approach to photometry of a number of stars from a number of images. There are two pieces:
I will describe first some requirements on the input data, and then show how to run these two program and interpret the results.
The input data is assumed to come from a set of N images. There must be a single ASCII text file per image which must include at least four columns of data for each star:
Any comment or header lines in the input files must begin with a pound sign character (#) in column 0, like this:
# Photometry of image 'M57.fts' # taken on 2004-Oct-12 02:23:05 UT # exposure time 30 seconds, R-band filter # xc yc mag magerr 50.1 201.2 12.34 0.02 127.8 33.9 12.85 0.04
By default, this package will give integer index values to each image to serve as "time" values: the first image will be "time" 0, the next "time" 1, the next "time" 2, and so forth. If you wish to attach a real time value, such as JD, to each image, create a column in each file for it. the "time" values ought to be identical for all measurements in the file, like this:
# An example showing a column for "time" value of the image
# ID Julian Data row col mag magerr
#
0 2450000.00000 13.48 16.43 10.0000 0.0500
1 2450000.00000 18.48 36.43 10.0500 0.0500
2 2450000.00000 23.48 56.43 10.1000 0.0500
The multipht program takes as input a set of data files, each of which has measurements of all the objects in one image. It produces as output a single, large ASCII text file with all the measurements, re-arranged so that all measurments of a single star are grouped together.
The usage is:
multipht [debug] [print] x= y= mag= err= [jd=] [auto] [list= ] [outfile= ]
[template= ] [matchrad= ] [min_match=] [quiet]
[star_cut= ] [image_cut= ] [isolate] file.pht ...
where options in brackets are optional.
They are
image23a.dat
image23b.dat
image39.dat
image43.dat
After reading input from each file, the program attempts to match detections of stars in different images. It assumes that all images have the same plate scale and orientation, differing only in a possible translation. First, the brightest MAXMATCH (defined in multipht.h) stars in each image are collected for matching purposes; all fainter stars are ignored. The matching algorithm picks one image as the "template". Stellar positions in all other images are compared to those in the template, one at a time. A brute-force algorithm considers all possible shifts which bring a star in the current image into registration with one in the template; for each possible shift, the positions of other stars are checked to see if they are within matchrad units of a star in the template. The shift which produces the largest number of matches between each image and the template is retained, and that shift is applied to all stars in the image. If a star matches more than one partner in the template image, it is assigned to the closest partner.
After the matching stage has finished, the program prints to stdout a list of the shifts required to bring each image into register with the template, like this:
lists QQ_input.000 QQ_input.001 dr = 0.96000 dc = -1.20000 10 of 10 lists QQ_input.000 QQ_input.002 dr = 1.61000 dc = 3.40000 10 of 10 lists QQ_input.000 QQ_input.003 dr = -0.56000 dc = 1.72000 10 of 10 lists QQ_input.000 QQ_input.004 dr = -1.75000 dc = -1.68000 10 of 10
The second column is the name of the template image ("QQ_input.000" in this example). The third column contains the name of the image being matched, the sixth and ninth columns the shifts required to bring the image into register. The final columns show how many of the stars in each image matched a partner in the template.
The next step involves choosing the stars and images to include in the ensemble. By default, the user must make decisions interactively. The program will display a histogram of the number of stars per image:
List of #stars, #images with that many stars
0 0
1 0
2 0
3 0
4 1
5 0
6 3
7 5
8 9
9 8
10 10
11 3
12 1
13 0
14 0
15 0
16 0
17 0
18 0
19 0
Enter cutoff for number of stars an image must have:
In this example, there is one image with 4 stars, three images with 6 stars, etc., up to a single image with 12 stars. The program asks the user to choose the cutoff for the number of stars an image must contain in order to be included in the solution.
Next, the program displays a similar histogram of the number of images in which each star appears:
List of #images, #stars that appear in that many images
0 0
1 5
2 0
3 2
4 0
5 0
6 3
7 4
8 7
9 9
10 10
11 5
12 6
13 0
14 2
15 0
16 0
17 0
18 0
19 0
Enter cutoff for number of images in which a star must appear:
In this example, there are five stars which occur in just a single image; in other words, there are give detections which cannot be matched to any other detections. Once again, the user must provide a cutoff value. Any stars which have fewer instances will be discarded from the ensemble.
If the user chooses the auto option, the program will pick cutoff values itself; see the STAR_CUT and IMAGE_CUT values in "multiweight.c". They are by default 25 percent of the maximum value. In other words, if the most commonly appearing star occurs in 40 images, then any stars appearing in fewer than 10 images (40*0.25) will be discarded.
Finally, if the auto flag has not been given, the program asks the user
do you wish to eliminate all saturated stars (y/n)?
Any measurement with an estimated uncertainty which is negative is assumed to be saturated. If the user replies "y" to this question, all such measurements are discarded from the ensemble. Otherwise, the negative sign is reversed and the measurement treated normally.
Any measurement with an estimated uncertainty of exactly zero is replaced with a small, non-zero value: see the #define macro MIN_MAG_UNCERT in multipht.h. We will later calculate the weight for a measurement based on the inverse of its (squared) uncertainty, so we can't permit a value of zero.
The output of the multipht program is a single file which contains all the measurements in the ensemble. The file has a three-part structure:
A very small ensemble might produce the following output. For clarity, I have added comments to delineate the sections; such comments do NOT appear in actual output.
# first comes the one-line header
2 images 3 stars
# next, a section describing the images
0 image0.dat 1.0 0.00000 3 3
1 image1.dat 1.0 1.00000 3 3
# now, a section describing the stars. Each star gets a line with
# its index value, X and Y coordinates, and number of measurements;
# then one line per measurement
0 13.48000 16.43000 2
0 0 13.48000 16.43000 0 10.0000 400.0
0 1 13.48000 16.43000 0 10.1000 400.0
1 18.48000 36.43000 2
1 0 18.48000 36.43000 0 10.0500 400.0
1 1 18.48000 36.43000 0 10.1897 400.0
2 23.48000 56.43000 2
2 0 23.48000 56.43000 0 10.1000 400.0
2 1 23.48000 56.43000 0 10.2000 400.0
The columns in the "image" section give the image index number, the name of the file with data for the image, the exposure time for each image (a dummy value, always 1.0), the "time" value for the image, the number of stars in the image which will be included in the ensemble, and the number of stars which matched a detection on the template (note that only a subset of all stars are used in the matching process -- see the value of MAXMATCH in multipht.h). The columns in the first line of each star stanza are the star index number, X and Y coordinate on the template, and the number of instances to follow; the columns on each subsequent line are the star index number, the image index number, the X and Y coordinates after having been shifted to best match the template, a flag to mark saturation (0 = not saturated, 1 = saturated), the magnitude value, and a weight based on the estimated magnitude uncertainty. Small uncertainties produce large weights.
This single file will serve as the input to the second stage of this package, the solvepht program.
The solvepht program takes as input a single large datafile with information on all images and measurements in the ensemble; it finds the optimal photometric solution and creates three output files with the results.
What does "optimal photometric solution" mean? We make several assumptions:
We have a large set of actual measurements m(i,j) of a number of stars in a number of images. Assuming that our model of the system is accurate, the error in each measurement must be
error(i,j) = m(i,j) - [ M(i) - e(j) ]
Our task is to find the image offsets e(j) and true magnitudes M(i) which minimize the remaining errors. The program uses standard least-squares techniques to find these parameters, then applies them to correct all measurements to the ensemble solution.
One invokes the solvepht program like so:
solvepht [debug] [infile=] [mconst=] [outfile=] [imfile=] [sigfile=]
[badim=] [badstar=] [varstar=] [min=] [max=] [varmin=]
[nsigma=] [niter=] [mrange[=low,high]] [irange[=low,high]]
[scatterbin=] [magmatch=] [minscatter=]
The arguments in brackets are optional;
those ending in equals signs require a value.
solvepht infile=multipht.out badim=3 badim=7 badim=23
solvepht infile=multipht.out badstar=8 badstar=12
solvepht infile=multipht.out varstar=32 varstar=1
mrange
then all non-variable stars between default values given by
#define MRANGE_LOW and MRANGE_HIGH in "solvepht.h"
(currently 1.0 and 2.5)
magnitudes below the brighest star are used to define
a shift; that shift is applied to all magnitudes
on output. If the user supplies values like so
mrange=2.0,5.0
the all non-variable stars with mean ensemble solution magnitudes
between these limits are used to define the shift
in magnitudes.
irange
then all non-variable stars with input magnitudes
between default values given by
#define IRANGE_LOW and IRANGE_HIGH in "solvepht.h"
(currently 8.5 and 10.0)
are used to define
a shift; that shift is applied to all magnitudes
on output. If the user supplies values like so
irange=2.0,5.0
the all non-variable stars with input magnitudes
between these limits are used to define the shift
in magnitudes.
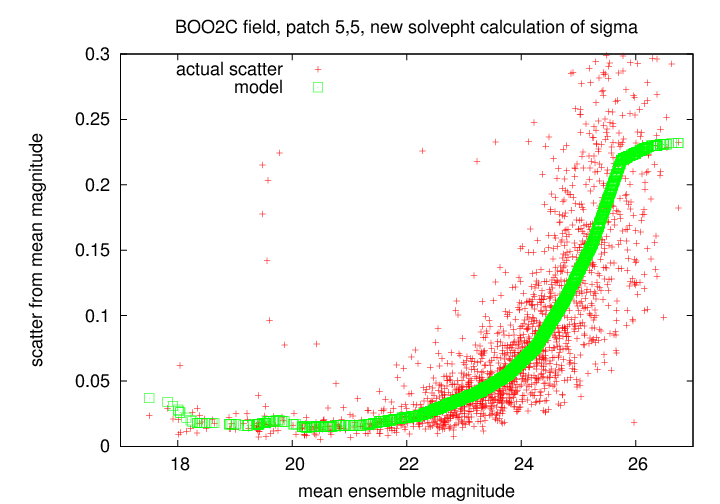
After the ensemble solution has been found, the program calculates at the scatter of each individual star from its mean solution magnitude. In general, this scatter is small for bright stars and large for faint ones, due to photon statistics. This shows clearly in the "sigma-vs-mag" plot used as a diagnostic for photometry:

The program fits a piecewise linear model to the locus of points in the diagram by dividing the stars into bins (of width scatterbin) by magnitude, calculating the median "sigma" value in each bin, and interpolating linearly between those points.
Stars which vary will appear as outliers in this "sigma-vs-mag" diagram: there are seven in the example above near magnitude 19.5, with scatter much larger than the model. The program attempts to identify variable candidates by calculating the distance of each star from the model fit, in units of the median model value. In the example above, the most variable star has a scatter of about 0.22 mag, while non-variable stars of similar brightness have a scatter of about 0.02 mag. It therefore has a "variability score" of about (0.22/0.02) = 11. Any star with a score larger than given by the nsigma= option (default value 3.0) will be marked as variable.
If the user supplies a value of niter= larger than zero, then the ensemble solution will be run more than once. Between each iteration, stars with high variability scores will be marked as "variable" and excluded from the ensemble calculations. In practice, a single extra iteration appears to suffice to remove the effects of clear outliers from the calculations.
The solvepht program creates three output files after a successful run:
corrected mag = m(i,j) - e(j)
A very small sample of the solvepht.out file looks like this:
0 35.32486 7.03099 72 2452263.62176 13.193 13.312 0.163 0 0.25 0 35.32486 7.03099 75 2452263.62706 13.193 13.322 0.171 0 0.25 0 35.32486 7.03099 104 2452263.67998 13.193 13.180 0.165 0 0.25 1 35.33325 6.72861 52 2452263.58649 11.360 11.333 0.079 0 -0.26 1 35.33325 6.72861 53 2452263.58825 11.360 11.351 0.081 0 -0.26 1 35.33325 6.72861 54 2452263.59001 11.360 11.350 0.081 0 -0.26 1 35.33325 6.72861 378 2453322.71022 11.360 11.491 0.065 0 -0.26 2 35.33335 7.18730 52 2452263.58649 12.190 12.202 0.104 0 -0.75 2 35.33335 7.18730 53 2452263.58825 12.190 12.196 0.101 0 -0.75
The columns are:
(*) During the matching procedure in multipht, the program calculates the mean shift in the X- and Y-directions which brings star into best registration with the template image. This shift is applied to each input position in the image and appears here.
A small sample of the solvepht.img file looks like this:
0 ./QQ_input.000 1.0 2450000.00000 10.000 0.009 0.002 1 ./QQ_input.001 1.0 2450000.01000 10.100 0.010 0.002
The columns in this file are
After finding the least-squares solution for zero-point values, the program judges them by calculating weighted sums for each image: given i=1..N stars in the image, it calculates two measures the degree to which all the stars in an image can be brought to match their true magnitudes.
let z = corrected_mag(i,j) - true_mag(i)
w = weight given to m(i,j) based on input mag uncertainty
[ sum (z*z*w) ]
z1 = [ ------------ ]
[ sum (N*w) ]
z1
z2 = --------------
sqrt (N)
The smaller the values of z1 and z2, the more closely the (corrected) measurements on this image match the overall ensemble measurements.
A small sample of the solvepht.sig file looks like this:
0 13.193 0.158 0 0.25 35.32486 7.03099
1 11.360 0.073 0 -0.26 35.33325 6.72861
2 12.190 0.078 0 -0.75 35.33335 7.18730
3 13.695 0.137 0 -0.84 35.34351 6.66053
The columns in this file are
Recall that by default, the output magnitudes are shifted so that the "true" magnitude of the brightest star is exactly zero. In the example above, the user must have used the mrange or mconst options to re-set them to larger values, closer to the input values.
In practice, using this package isn't all the complicated. I use it myself to analyze photometry of fields containing variable stars for the Center for Backyard Astrophysics. For example, let me explain in some detail the results for one particular night: Oct 5, 2004.
I took a series of 115 images of the cataclysmic variable star ASAS 002511 and its neighbors. After the usual dark subtraction and flatfielding, I extracted positions and instrumental magnitudes for every object detected in every frame; that added up to 6211 detections.The raw instrumental magnitudes for each image were stored in a series of 115 files; here's a sample of one:
1 4.28 461.12 3325 13.48 14.836 0.049 14.818 0.057 4
2 11.53 32.51 3339 13.88 15.330 0.076 15.287 0.086 0
3 36.66 240.87 3335 14.65 14.648 0.041 14.626 0.048 0
I created a file with the names of these files, one per line. I ran multipht with a command line like this:
multipht list=asas.lst x=1 y=2 mag=6 err=7 outfile=multipht.out
I answered the questions to select cutoffs for the number
of stars required in an image (10) and number of detections
required for a star (10) to be included in the solution.
The result was a big output file, multipht.out.
The second stage of the analysis is more complicated; it usually takes me several passes through the dataset. I ran the solvepht program an initial time to get a feeling for the overall properties of the images and stars. I first examined the solvepht.img file, plotting the zero-point value versus "time". I saw that the zeropoints of most of the images followed a gradual trend (due to the changing airmass of the field), but there were occasional outliers. Some of these were due to poor tracking (on a trailed image, all the stars look fainter than normal), others due to passing clouds. I wrote down the index numbers of the bad images so that I could remove them from the solution during the next pass.
I also looked at the solvepht.sig file, plotting the uncertainty in ensemble magnitude versus true magnitude. You can see a version of this graph on the web page describing this night's results. Most stars fall in a line which curves gently upward to the right: fainter stars have larger scatter in magnitude. On the first pass, a number of objects appeared far above this normal locus: one of them was a real variable star, but others were stars with bad measurements: some close to the edge of the frame, others part of close pairs, others falling near defects on the chip, etc. I noted the index numbers of these objects, dividing them into "obviously bad objects" and "possibly true variables".
I then made a second pass, running solvepht again with extra arguments. Here's the command line:
solvepht infile=multipht.out outfile=solvepht.out imfile=solvepht.img
sigfile=solvepht.sig varstar=13 badim=15 badstar=32
badstar=29 badstar=38 badstar=49
This indicates that I removed one image and four stars from the solution, and marked one star as "variable." That star (which was the known variable ASAS 002511) was not used in deriving the ensemble solution, but it was retained in the output.
In most cases, I make three or four passes through the dataset, gradually placing more and more stringent requirements on the stars and images. It helps to make a small shell script with the command line for solvepht so that one can quickly add or subtract a few more bad stars and images.
After I was satisfied with the results, I finally looked at the solvepht.out file. I picked out individual stars by choosing all lines which started with a particular value, then made a graph showing each star's corrected magnitudes versus time. You can see a light curve of four objects in the field near the bottom of the web page describing this night's results. The three non-variable stars are indeed not changing relative to each other, and the faintest in the group has the largest scatter. The fourth object, shown as green crosses, is the variable star. It is clearly varying more than one would expect for a star of its apparent brightness, just as the plot of scatter-versus-magnitude indicates.
Last modified by MWR 8/10/2015