
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomers have determined that the universe is about 13.7 billion years old using several methods. The value is pretty well accepted, and different studies over the past decade yield roughly the same number.
But how? How can scientists measure such a gigantic stretch of time? How good is the evidence?
One of the central pillars of this age is a method known as radioactive dating. Let's look at the basic idea behind it, using a technique applied to objects only a few thousands of years old; we can then see how similar methods can be used to measure the ages of rocks and planets and even stars.
Atoms are the basic units which make up materials in the world: rocks, plants, air, people -- they are all made out of atoms. Each element, such as carbon, oxygen, iron, and so forth, are composed of a different type of atom.
But atoms aren't the smallest bits of matter; inside each atom are a number of sub-atomic particles. The most common of these are
So, for example, the most common type of carbon atom contains 6 protons, 6 electrons, and 6 neutrons. Very neat and symmetric. We call this sort of atom "Carbon-12", often written 12C. The protons and neutrons clump together at the center of the atom, in what we call the nucleus. The electrons fly around the nucleus, sort of like little tiny planets orbiting a little tiny star.

But there are other varities, or "isotopes", of carbon atoms. All carbon atoms must have 6 protons and 6 electrons, but they can have slightly different numbers of neutrons. For example, one very rare isotope of carbon is Carbon-14: it has two extra neutrons.
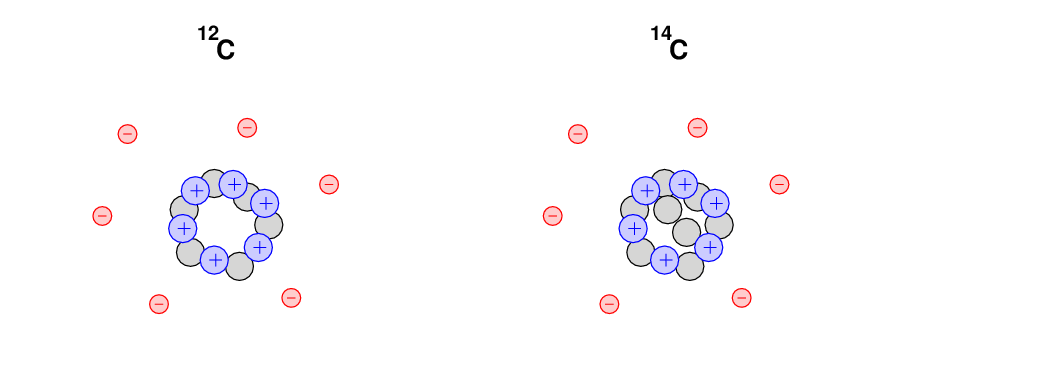
The Carbon-14 atoms are very, very uncommon: only about 1 carbon atom in a trillion has these two extra neutrons. However, these atoms are well mixed together with the ordinary variety in the air we breathe and in the food we eat. In every bite of an apple, we ingest lots of 12C and a few 14C. So, as humans live and eat and go to class, their bodies incorporate lots of carbon atoms into bones and muscles and tissue. One in a trillion of those carbon atoms are of the 14C variety.
However, there is one very big difference between the ordinary 12C and the few 14C atoms in your body: the 12C atoms are stable, but the 14C are unstable. Every now and then, an individual 14C atom will radioactively decay: one of its neutrons turns into a proton plus an electron.
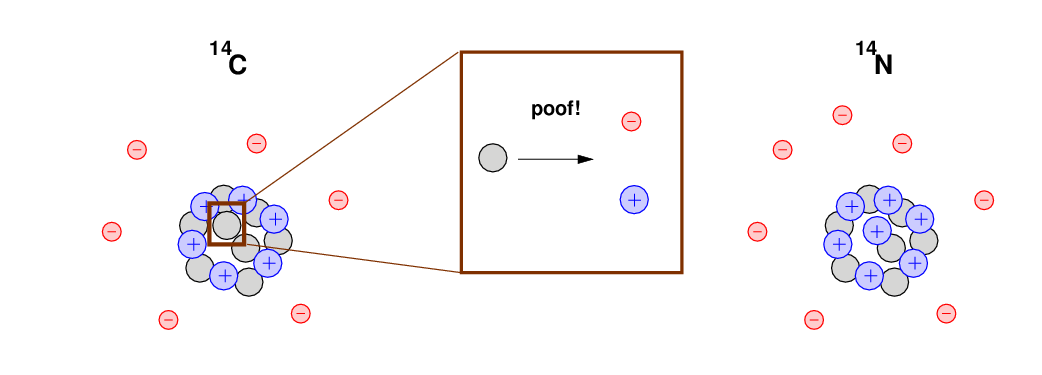
The result of this decay is an atom which now has 7 protons, 7 electrons, and 7 neutrons: no longer a carbon atom, it is now an atom of nitrogen; Nitrogen-14, to be specific, or 14N for short.
Fortunately for us (and plants, and animals), Nitrogen-14 atoms behave very politely inside our bodies. The occasional transformation of one little carbon atom into one little nitrogen atom does not cause any big chemical changes, and life goes on as normal.
So, if you look inside a living person (or plant, or animal), you'll find lots and lots and LOTS of carbon atoms. The great majority will be the common 12C, and about 1 in a trillion will be 14C.
Just how frequently do carbon atoms turn into nitrogen atoms? Well, if you look at any particular 14C atom, it might decay in 12 minutes, or 5 years, or 15,000 years, or 180,000 years; the exact time is completely random and unpredictable, as far as we can tell. But if you look at a BIG SAMPLE of 14C atoms, you will find a clear pattern (if you can wait long enough): after 5,730 years, HALF of the sample will have turned into nitrogen atoms. Then, after another 5,730 years, half of the REMAINING 14C atoms will have turned into nitrogen. And after another 5,730 years, half of those which remain will have decayed.
If one starts with a sample of 100 14C atoms ...
after this many years this many 14C remain
--------------------------------------------------------
0 100
5,730 50
11,460 25
17,190 12
22,920 6
--------------------------------------------------
Physicists use the term half-life to describe the process: the half-life of 14C is 5,730 years.
So how can we use this information to determine the age of some old item? Say, for example, this flute made from the bone of a large bird, found in a cave in Germany.

Image credit
Conard, Malina and Munzel, Nature 460, 737 (2009)
Well, in the same cave, archaeologists found many other bones and bits of charcoal. Way back in time, as the animals and plants in this area grew, they extracted carbon atoms from their meals and from the air in order to build new cells and structures. Most of those were 12C atoms, but about 1 in a trillion were 14C.
When the animals and plants were killed by humans and brought into this cave, they stopped inhaling and ingesting carbon atoms. At that point, carbon atoms inside the bones and charcoal were fixed in place, with the standard ratio of 1 14C to one trillion 12C. That was the ratio of carbon isotopes in the bones when they were dropped onto the floor of the cave and forgotten.
But then what? As time passed, and the bones were buried until layers of dirt and sediment inside the cave, some of the 14C atoms inside them began to decay. That made the ratio of Carbon-14 to Carbon-12 start to decrease. As more and more time passed, more and more of the 14C turned into 14N.
When archaeologists tested bits of the bones from this cave in the year 2009 (see Conard, Malina and Munzel, Nature 460, 737 (2009)), they found that the ratio of 14C to 12C was no longer the standard of 1 in a trillion; instead, it was closer to 0.013 in a trillion.
Q: How old are the bones, and the flute?
The particular method of Carbon-14 decay won't work to figure out the age of the Earth or the Moon, because the half-life of Carbon-14 is just too short. After ten half-lives of 14C, which is about 57,300 years, only (1/2)10, or about 1/1000, of the original sample of Carbon-14 atoms will remain. After another ten half-lives, so a total of slightly over 100,000 years, only (1/2)20, or about 1/1,000,000 of those Carbon-14 atoms will be left. That's just too few to detect, in most cases; and going back only 100,000 years isn't close to enough to measure the age of our planet.
In order to measure ages of millions or BILLIONS of years, we need to find atoms which decay much more slowly. Fortunately, there are a number of possibilities which involve (relatively) common elements with very long half-lives. Just a few are listed below -- thanks to the US Geological Survey.

Table courtesy of
US Geological Survey
We can use samples taken from rocks and minerals on Earth to measure the ages of those samples. One of the oldest big chunks of solid material we've found so far is this rock from Canada, which solidified around 3.96 billion years ago.

Image courtesy of
the American Museum of Natural History
The zircon crystals in this pebble are even older: at roughly 4.3 billion years old, they are among the oldest items known to have formed here on Earth.

Image courtesy of
the American Museum of Natural History
Thus, we can deduce that the Earth itself must be somewhat older than 4.3 billion years.
We can apply similar techniques to rocks from the Moon. Barboni et al. (Science Advances, 3, e1602365, 2017) use the ratio of uranium to lead in zircon crystals collected by astronauts to determine an age of the Moon of about 4.5 billion years.
Now, when it comes to stars, this method runs into some problems. First, we can't just dig a chunk of material out of any star and bring it back to the lab. As we'll see in a future lecture, though, it is possible to analyze the light from a distant star via a technique called spectroscopy in order to measure the abundance of elements in its atmosphere. That's the good news.
The bad news is that pretty much all the elements which have half-lives long enough to measure timescales of billions of years are
It turns out that even our best measurements of stellar ages by the radioactive decay method yield only very approximate ages.
How approximate? Look at the table below. It lists ages measured for three different stars, using a variety of parent/daughter pairs of elements. Different methods applied to the same star OUGHT to yield the same age ... but, as you can see plainly, they don't.
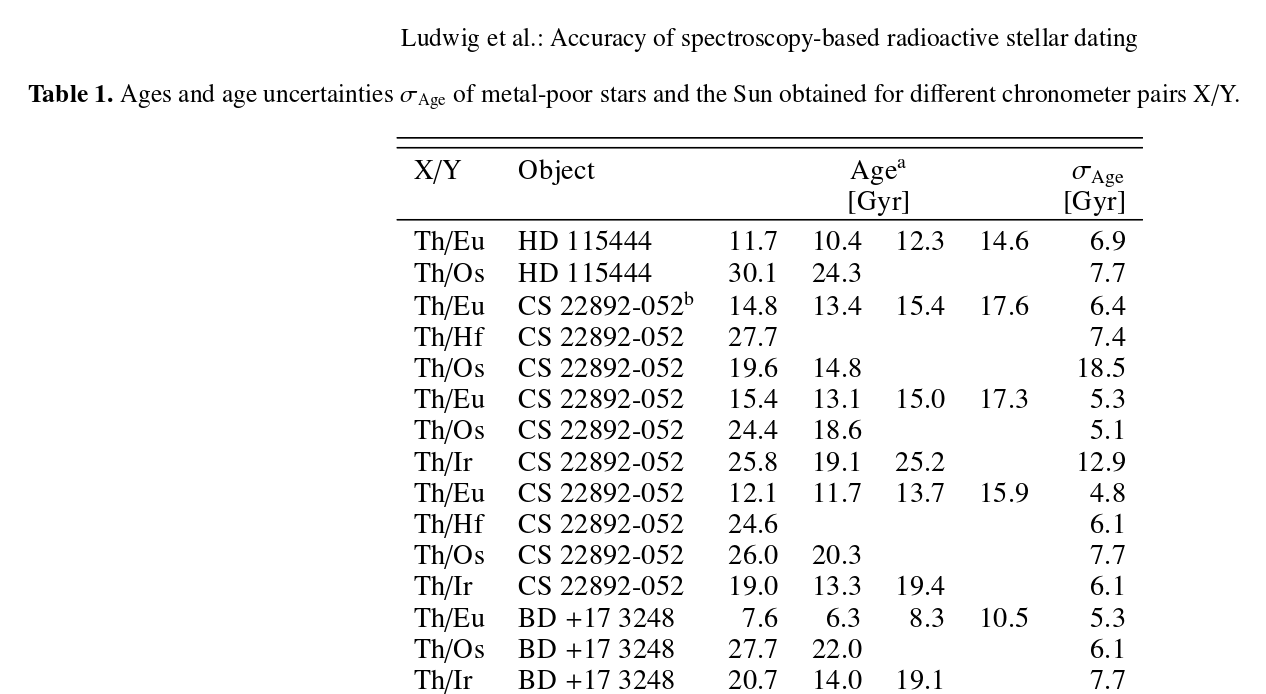
Image taken from
Ludwig et al., A&A 509, 84 (2010)
Despite these problems and low precision, astronomers have decent evidence that the oldest stars we have found are something like 10 or 15 billion years old.
Age of oldest stars (based on radioactive decay) = 10-20 billion years
There is another method for estimating the ages of stars. It is much less directly based in fundamental physical principles than the radioactive method, but can applied much more widely, to many more stars. The basic idea is to build models of stellar interiors in a computer: break up a star into a series of shells, and pretend that the temperature, density, chemical composition, and other properties, are constant within each shell.
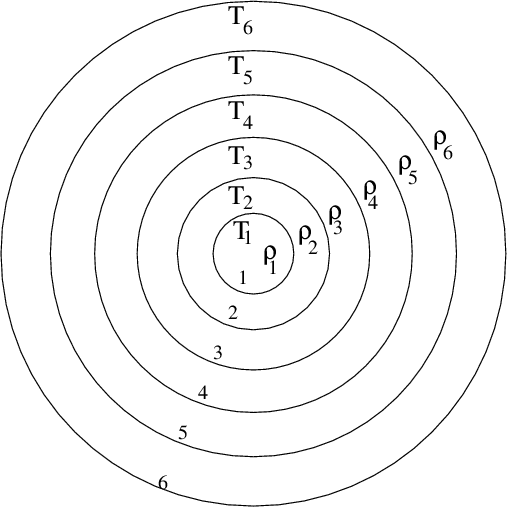
In the center of the star, nuclear reactions occur, converting light elements such as hydrogen into heavier elements such as helium.
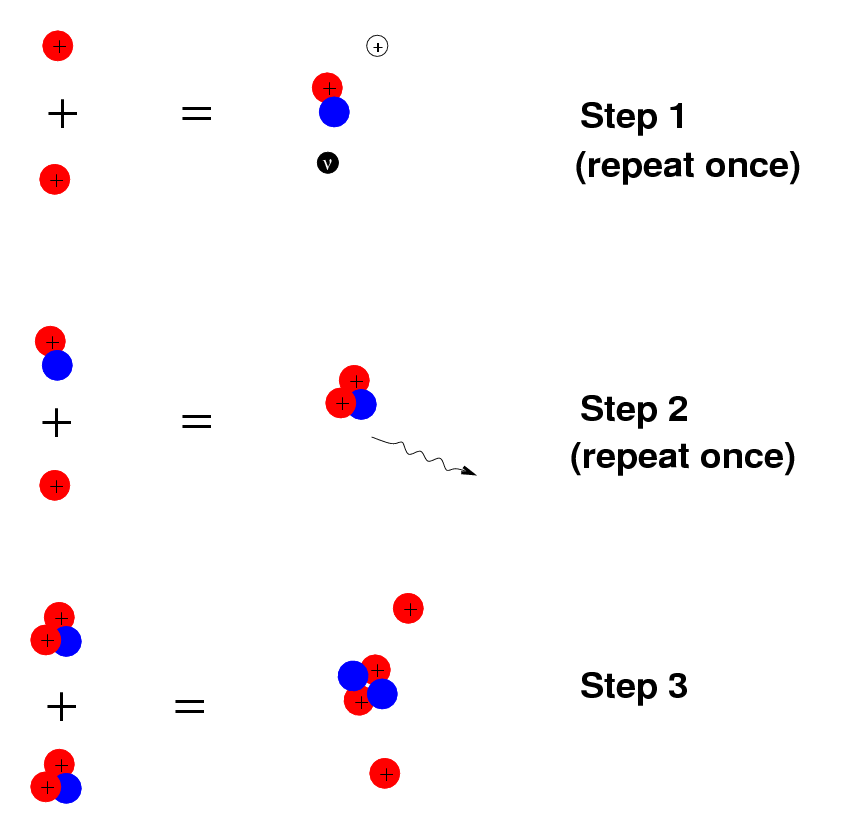
We can figure out how many of these nuclear reactions must be going on at the center of the star, and follow the flow of energy through the layers of the star and out into space. Inside a computer, we can allow time to pass very quickly, and watch how the star evolves, changing its size and temperature and luminosity as it runs through all the nuclear fuel in its interior.
(click on the image below to activate the animation)
We can compare our stellar models to real stars to some extent, in order to check that the models are accurate; but since it takes millions or billions of years for real stars to evolve, and humans don't live that long, we are always making some assumptions and approximations. Nonetheless, we THINK that our current stellar models are pretty good: certainly good enough to estimate ages to 20% or so, and perhaps a bit better.
What are the ages of the oldest stars according to our stellar models?

Abstract of
Bond et al., ApJ 765, 12 (2013)
Age of oldest stars (based on models) = 12-14 billion years
Another way to estimate the age of the universe involves its expansion and global properties. When we look at distant galaxies, we see that they are all flying away from us. That's not because we some special planet, located at the center of the universe; its due to the general expansion of the universe.
If we run this expansion backwards in time, we can very roughly estimate the time since the universe was very dense and very hot -- since the Big Bang, in other words. And the best estimates for the age of the entire universe are around
Age of universe (based on expansion) = 13.7 billion years
It's easy enough to write the age of the universe -- 13.7 billion years. There. Done. But how long is that, really?
One way to try to grasp such a profoundly long stretch of time is to compress it into a more familiar item: the year. We all have a pretty good idea for the length of a year, and its subdivisions: months, weeks, days, and so forth. By squishing all the events which have occured during the lifetime of the universe into a single calendar year, we will create a cosmic calendar. Let's give it a try.
You can find one version of this calendar inside the front cover of the recommended textbook, but it will be more fun if we make our own. Here's a copy of the 2020 calendar, thanks to calendar-365.com, to help you remember how many days are in each month.

Calendar thanks to
calendar-365.com
Q: Suppose we map 13.7 billion years into 365 days.
What length of real time does a single "cosmic day" represent?
Q: Suppose we map all the time within a single "cosmic day"
into 24 "cosmic hours". How long is a "cosmic hour?"
Q: Suppose we map all the time within a single "cosmic hour"
into 60 "cosmic minutes". How long is a "cosmic minute?"
Q: Suppose we map all the time within a single "cosmic minute"
into 60 "cosmic seconds". How long is a "cosmic second?"
Okay, I think we're ready now. Below, I've listed some events in the history of the universe, or the solar system, or the Earth. Your job is to figure out on what date of the cosmic calendar each event would occur; if you wish, you can figure out the rough time of day for the event, too. Remember,
Event Years ago Date (and time)
in real time on cosmic calendar
------------------------------------------------------------------------------
first stars form 13.5 billion
solar system forms 4.6 billion
Earth forms 4.5 billion
first fossil life 3.5 billion
first vertebrates 530 million
plants on land 470 million
insects colonize land 412 million
amphibians on land 363 million
first dinosaurs 230 million
K-T extinction 66 million
humans build fire 1.5 million
Lascaux cave paintings 17,000
birth of Roman Empire 2,045
USA declares independence 242
------------------------------------------------------------------------------
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.