
Image credit: ESO/M. Kornmesser
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

Image credit:
ESO/M. Kornmesser
On August 24, 2016, the European Southern Observatory announced the discovery of a planet around Proxima Centauri. Not only is this the star closest in space to our Solar System, but the planet was said to be within the star's habitable zone.
The news made headlines around the world. Within days, people were dreaming of ways that we could visit this new world.

Image courtesy of
the Breakthrough Initative
There are many questions:
Throughout the next eight weeks, we will discuss the methods by which astronomers detect planets orbiting around other stars, and measure their properties. As we proceed, we may encounter Proxima Centaur and its putative planet again.
So, if you hear any interesting news about
Proxima Centauri b, or any other exoplanets,
PLEASE LET ME KNOW!
I hope that we can discuss the latest news
from exoplanet discoveries in this class.
The simple answer is
An exoplanet is a planet orbiting a star other than our Sun.
However, that presumes that we all agree on the definition of a "planet" -- which may not be true.
So, let's pause for a moment to talk about the meaning of "planet", and then come back to our main topic of "exo-planets".
We can choose to make this an easy question, or we can try to be "official" and make it difficult.
An easy answer is to take the approach of the United States Supreme Court Justice Potter Stewart: in the case of Jacobellis vs. Ohio (1964), which involved the banning of an "obscene" movie, Stewart wondered how one could define "obscenity" in a film:
"I shall not today attempt further to define the kinds of material I understand to be embraced within that shorthand description; and perhaps I could never succeed in intelligibly doing so. But I know it when I see it, and the motion picture involved in this case is not that."
So, here are some pictures of objects in our Solar System. You decide: Planet, or Not Planet?
| Planet | Not Planet |  |
| Planet | Not Planet |  |
| Planet | Not Planet |  |
| Planet | Not Planet |  |
Well, it seems that the method "just look at it" works in most cases, but not all of them. The common features of a planet are:
The difficult criterion is the last one: how big is "big enough?"
If we look back through history, we can see that scientists have changed their minds. Click on the graph to see what was happening.
The number of planets held steady at 9 for a long time, from 1930 to the early 2000s. However, starting in 1992, astronomers started to find relatively large bodies in the outer reaches of the solar system, which came be known as "Kuiper Belt Objects" (KBOs). Some of these objects turned out to be roughly the same size as Pluto. If Pluto was a planet, shouldn't some or all of these big KBOs also be called planets?
In 2006, the International Astronomical Union (IAU) passed a resolution to settle the matter. After some acrimonious debate, a small subset of astronomers (those who were still present at the meeting on its last day) approved the following definition:
A planet is a celestial body that
(a) is in orbit around the Sun,
(b) has sufficient mass for its self-gravity
to overcome rigid body forces so that it
assumes a hydrostatic equilibrium (nearly round) shape, and
(c) has cleared the neighbourhood around its orbit.
Now, again, the first two of these conditions are pretty clear, but the third is again ambiguous. What does it mean to clear the neighborhood around its orbit? A planet must be much bigger than any other body which has a similar orbit ... but how much bigger? And how similar an orbit?
One way to define mathematically the meaning of clear the neighborhood around its orbit is to estimate the time it takes for a large body of mass M orbiting a star with some period P to eject smaller bodies in its vicinity due to gravitational forces during close encounters.
Consider the large body to have orbital radius a and the smaller body nearby to orbit with a radius which differs by Δa.
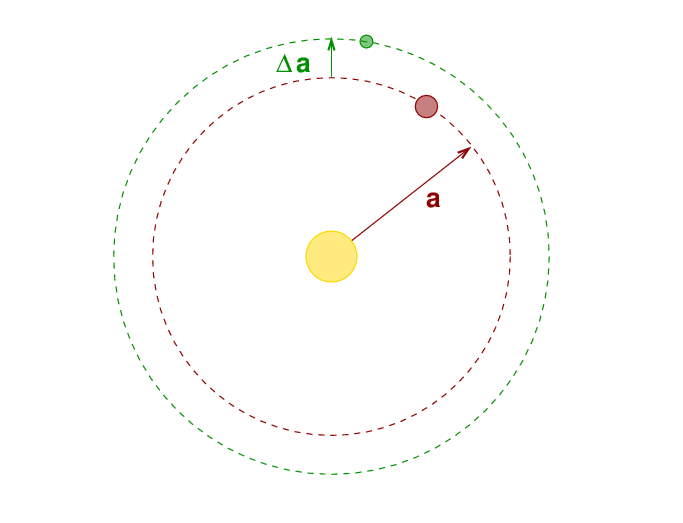
Since the bodies have different orbital radii, they will move with different speeds and periodically catch up to each other. During these close encounters, the massive object may perturb the other body's motion significantly. Let's zoom into a view centered on the massive object:
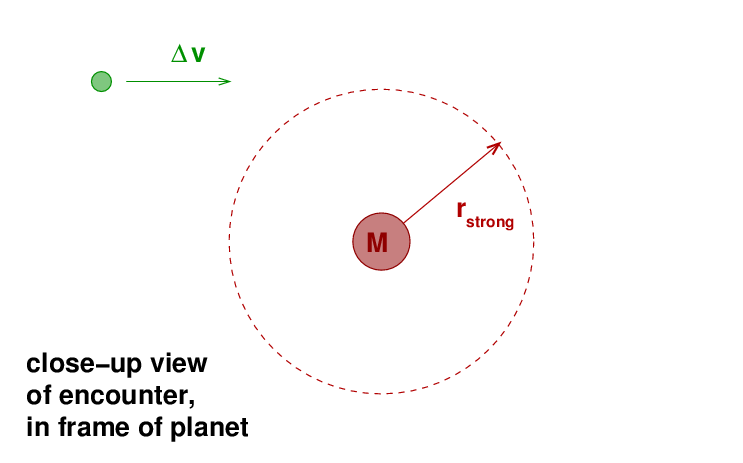
In this frame of reference, the massive body sits motionless while the other object drifts past at relative speed Δv. If the closest approach is small enough, the gravitational force may fling the other body out of its orbit. The questions are:
Some scientists have examined these questions very carefully; for example, see
I'll just do a very quick, order-of-magnitude analysis here.
To answer question (1), "how close must the encounter be?", let's say that if the magnitude of the gravitational potential energy of the two objects is larger than the kinetic energy of the small body in the planet's frame of reference, then the small body will be significantly scattered from its original orbit.
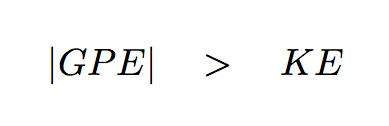
Q: Derive a relationship between the critical radius
rstrong and the relative speed Δv.
Right.
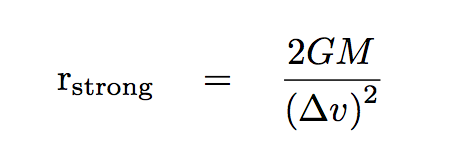
Let's write that relationship down and save it for just a moment.
The second question is "how frequently do such close collisions occur?" We can use a common approach to estimate this frequency -- the same method physicists use to figure out how often particles in a gas will collide, or how far a photon can travel through a cloud of atoms.
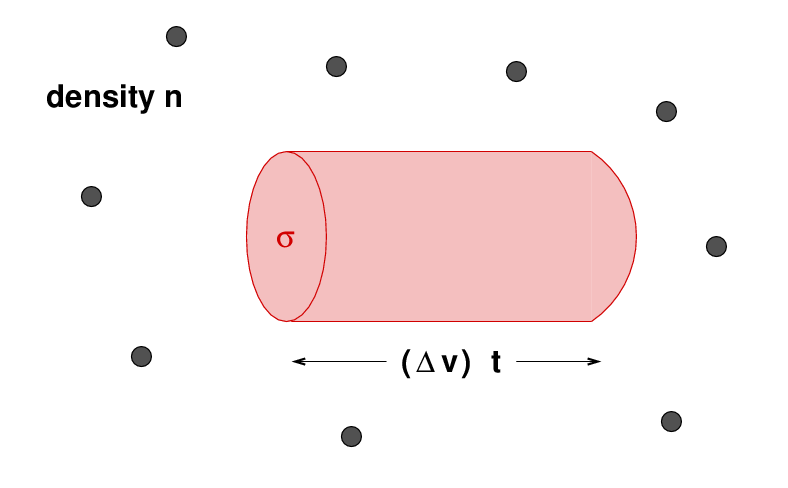
The equation is
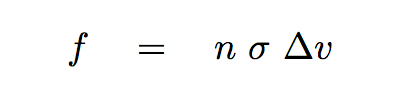
where
f is the frequency of collisions
n is the number density of small bodies
σ is the cross-section "gravitational area" of the planet
Δv is the relative speed of the small bodies
The cross-section area σ is simply
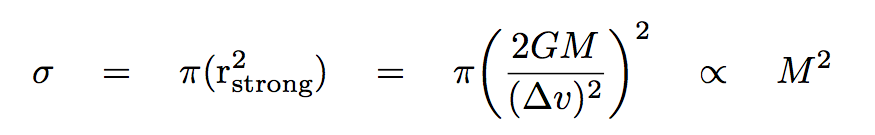
which tells us that the frequency of strong collisions depends on the mass of the planet SQUARED.
The relative speed of the two objects Δv is a function of the difference in their orbital radii, Δa. For circular orbits, it is possible to show that this DIFFERENCE in speeds is inversely related to the period P of the planet's orbit:
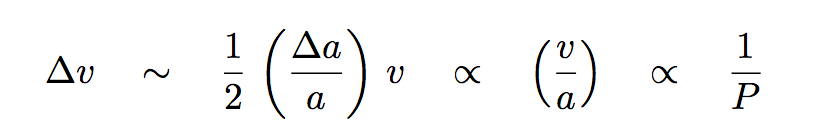
And so (finally), we can put the frequency of strong encounters between a big planet and small bodies nearby into a quantitative form like so:
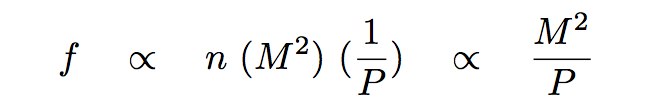
The TIMESCALE for a massive planet to scatter smaller bodies away from nearby orbits -- in other words, the timescale for a planet to clear its neighborhood -- is inversely proportional to this frequency of close encounters. We can therefore define a quantity which expresses this timescale like so:
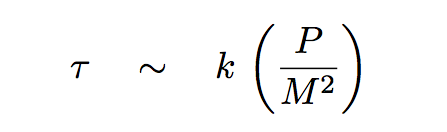
Strictly speaking, this is the timescale for having an encounter with one small body and ejecting it; so, if there are many small bodies near a large one, the total time to "clear the neighborhood" will be considerably larger ... but this gives us a very rough idea.
Phew. That was a lot of work, but it means that we can now compare bodies in the solar system using this quantity to compare the times each object would take to "clear the neighborhood." Let's do it!
Following Goldreich et al. (2004) and Soter (2006) , one can show that the constant k in the equation above has a value in our Solar System which is very roughly
k = 1054 kg2
if the mass M is expressed in kilograms.
Now, let's work together to fill in this table.
Body Mass (kg) Orbital Period (yr) time to eject (yr)
--------------------------------------------------------------------------
Mercury
Venus
Earth
Mars
Ceres
Jupiter
Saturn
Uranus
Neptune
Pluto
Eris
--------------------------------------------------------------------------
The times to eject neighbors have quite a large range. It may clarify things to show them graphically:
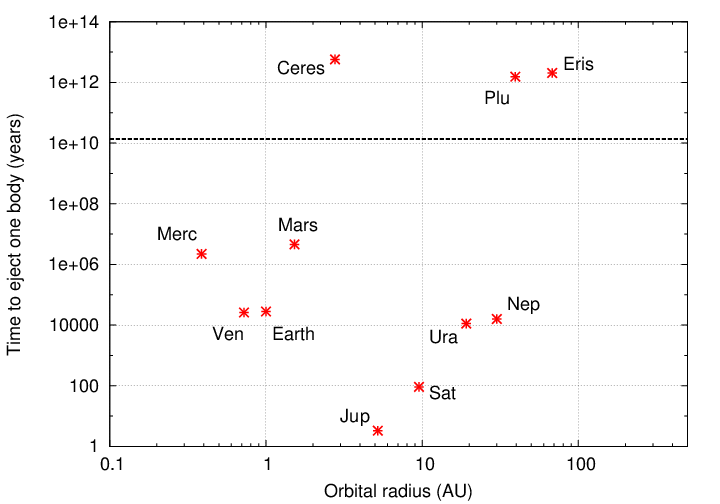
Yes, it's clear that these objects fall into groups with a LARGE separation. Nearly five orders of magnitude -- 100,000! -- separate Ceres, Pluto and Eris from the larger bodies. The dashed line shows the age of the universe; note that objects above the line have not been able to eject small bodies from their regions of the Solar System.
It seems eminently sensible to use a criterion such as this to classify bodies in the Solar System as "planets" and "not-planets."
Now that we know the IAU definition of "planet", we could claim that an "exoplanet" is just an object orbiting some star other than the Sun, which satisfies the criteria (b) and (c).
(b) has sufficient mass for its self-gravity
to overcome rigid body forces so that it
assumes a hydrostatic equilibrium (nearly round) shape, and
(c) has cleared the neighbourhood around its orbit.
We might have trouble with item (b), since it isn't easy to discern the SHAPE of a body orbiting another star ... but we could make a reasonable guess based on the object's mass and radius, which are easier to determine.
That approach would be logical. But, in the world of "official" definitions, logic is not always in charge. At the current time, the IAU has not passed any resolutions which explicitly define the term "exoplanet."
But I'll adopt the following working definition for the remainder of this course. It's simpler than the IAU definition for "planet" because we usually have only small bits of information.
An exoplanet is
(a) a body orbiting a star other than the Sun
(b) not in orbit around a non-stellar body
(this excludes "exo-moons")
(c) with a mass less than the critical limit (approx 13 Jupiter masses)
for hydrogen fusion in its core
Note that the official definition of "planet" does not include the upper limit on mass, and this working definition says nothing about hydrostatic equilibrium or "clearing the orbit." Margot (2015) has checked the properties of known exoplanets and found that the great majority SHOULD have cleared their orbital zones.
So, time for a "trick" question:
Q: When was the first exoplanet discovered?
There are at least three answers, depending on exactly what one means by "first exoplanet discovered." The contenders are:
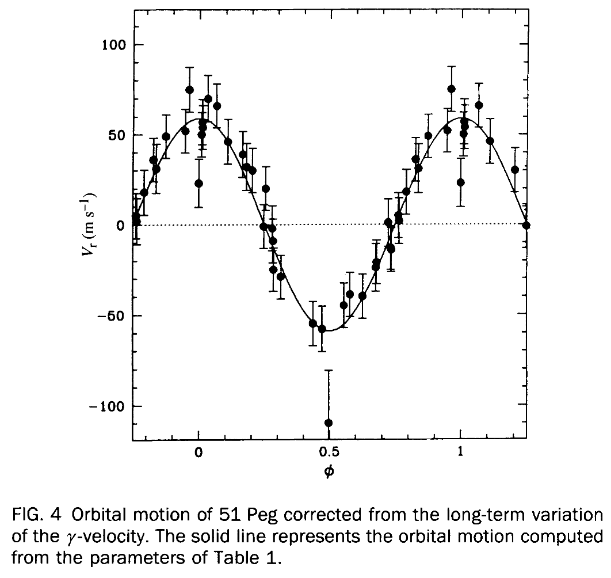
Figure 4 taken from
Mayor and Queloz, Nature 378, 355 (1995)
Radio astronomers monitoring the "blips" coming from one particular pulsar noticed that the pulses were sometimes arriving a little earlier than expected and at other times a little later -- where "a little" means "a few milliseconds." Radio astronomers are very good at measuring time!
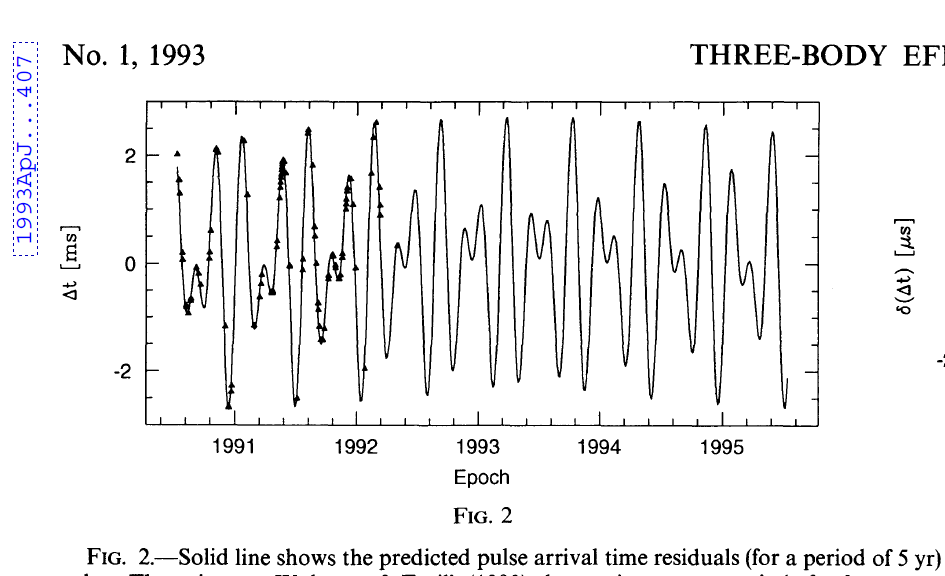
Figure 2 taken from
Malhotra, ApJ 407, 266 (1993)
These variations were attributed to the displacement of the pulsar by the gravitational pull of 2 small objects (a third was added a few years later). The discovery was a major surprise to most astronomers. How could any planets survive the supernova explosion which created the pulsar? The two bodies were both roughly the mass of the Earth, but what would conditions be like on them?
It didn't help that these two objects were discovered by accident -- not as part of a dedicated search for extrasolar planets. Many people simply forget about them, or lose interest because it seems pretty clear that the chances of finding life on them are tiny.
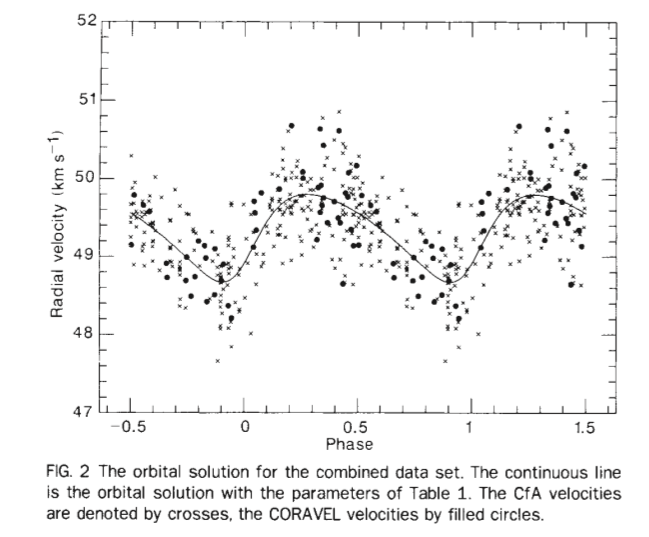
Figure 2 taken from
Latham et al., Nature 339, 38 (1989)
The authors realized that the perturbing object might have a mass small enough to prevent it from fusing hydrogen, and so it might be a planet ... but they noted that without a measured inclination for the orbit, it might very well NOT be a planet:
This leads to the suggestion that the companion is probably a brown dwarf, and may even be a giant planet. However, because the inclination of the orbit to the line of sight is unknown, the mass of the companion may be considerably larger than this lower limit.
Continued monitoring of the host star (for example, Kane et al.) have failed to detect transits of HD 114762 by this orbiting body, and so we still don't know the inclination. Since the lower bound on the object's mass does (barely) fall within the planetary range, some lists and databases do call it a "planet."
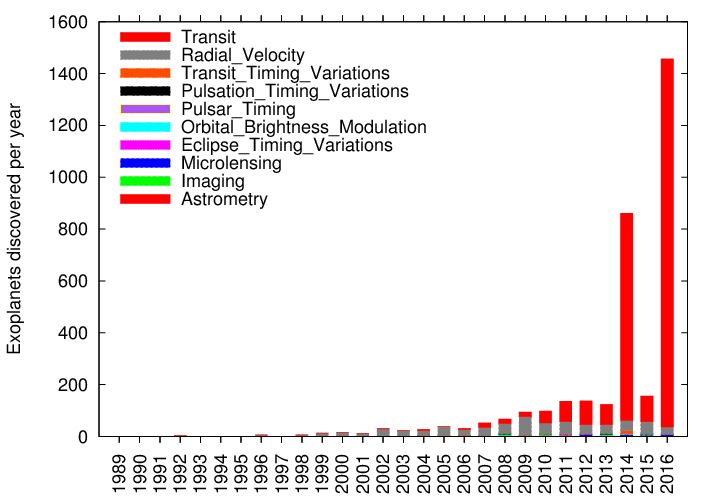
The first exoplanets were found roughly 20-25 years ago. What has been happening since that time?
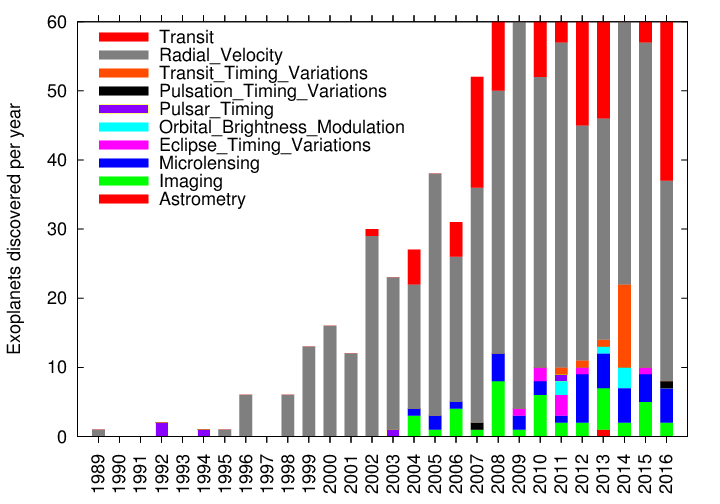
Astronomers have been finding many, many more exoplanets! Notice the large number of methods; we'll discuss most of them in this course at least briefly.
Even though there are many methods, it turns out that two of them are by far the most productive: radial velocity and transits. We'll spend quite a bit of time examining these two techniques. The transit method, in particular, has been VERY fruitful in the last few years.
Q: Why have so many exoplanets been found by
the transit method?
Q: Did something special happen in 2014?
Q: Did something special happen in 2016?
In 2014, Kepler scientists released the results of two years of monitoring the Kepler field; in addition to incorporating new data, the study applied new techniques to some of the earlier measurements. The result was a big burst of exoplanet discoveries:
And yes, in May 2016, just a few months ago, the Kepler team announced results based on an automated re-analysis of all the Kepler data collected so far.
Please give your name-card to the instructor before you leave today.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.