 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So, you've computed the starting energy in your gravitational simulation, and then you let the planets run for 10,000 years. At the end of the simulation, you compute the final energy of all the bodies. When you compare them, you find that the final energy is larger by 1 percent.
What can you do?
First, you should think for a moment -- does this really matter? For some purposes, it might not. Look around: are all the planets still in orbit around the Sun? Have any of their orbital radii changed in an obvious manner? What was your goal? If you wanted to find out whether Uranus would be on the same side of the Sun as the Earth in July, AD 12,011, maybe you can answer your question just fine, even with the change in energy.
But suppose that you decide this change in energy is NOT acceptable. Perhaps your goal was to look for very small changes in the orbital radius of the Earth over time, to compare against fossil records. In that case, you might need precisions of 0.01 percent in the orbital radius. An error of 1 percent in the total energy is a sign that you are in trouble.
Congratulations! You have just completed the first step in your recovery process: recognizing that there is a problem.
One way to fix the problem is simple: continue to use a fixed timestep throughout your program, but this time, when you run the program, specify a smaller timestep. After the program finishes, you can once again compare the initial to the final energy, and decide if the result is accurate enough for your purposes.
That manual approach will work, but it could take quite a bit of your time. Suppose that each run requires 2 hours; then you might be going back to the computer every 2 hours, doing a comparison of original and final energy, and deciding if you can accept the result. If the job is due tomorrow morning, you have time to go through only 3 or 4 iterations.
A better approach is to automate the entire procedure, so that your program will automatically vary the stepsize in order to reach some pre-set limit on the change in energy. Consider the following pseudocode:
set tolerance = 0.001
set timestep = t_initial
TOP
compute initial total energy Ei
time = starting_time
while (time < ending_time)
compute new position and velocity of all objects
update position and velocity of all objects
time = time + timestep
end
compute final total energy Ef
frac = (Ef - Ei) / Ei
if (frac > tolerance)
timestep = timestep / 2
goto TOP
else
finish
This design uses the same timestep throughout the entire simulation, waits until the end, and then checks to see if it should re-run the simulation with a smaller timestep. This ought to work, but it might take quite a while to figure out the appropriate timestep.
Q: Suppose that each run requires 5 hours;
if the initial timestep is 32 times larger
than the smallest acceptable timestep,
how long will it take for your program
to end up with the correct result?
Another approach is to adjust the size of the timestep within the main loop of the program itself. The pseudocode for that approach might look like this:
set tolerance = 0.001
set timestep = t_initial
TOP
compute initial total energy Ei
time = starting_time
while (time < ending_time)
compute new position and velocity of all objects
compute current total energy Ec
frac = (Ec - Ei) / Ei
if (frac > tolerance)
timestep = timestep / 2
else
update position and velocity of all objects
time = time + timestep
end
end
In this case, some steps might be bigger than others.
Q: In the example immediately above, I set
the tolerance variable to the
same value, 0.001, as in the first example.
Is that the right thing to do?
We've discussed here the idea that one might decrease the size of the timesteps used to advance the positions of objects in a gravitational simulation. But there are other ways that numerical simulations can be made "finer" in order to improve their performance.
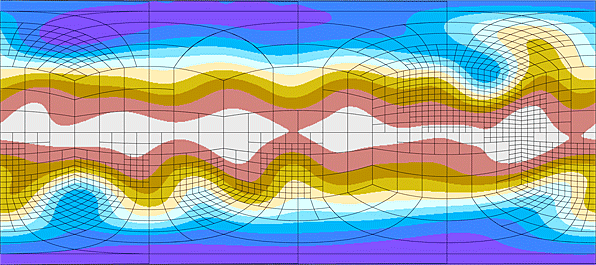
For example, suppose that we want to simulate the impact of flowing air on a mountain which sticks up from the surrounding plane. There will be some regions far from the mountain in which the airflow will be smooth: the velocity of air HERE will be almost exactly the same as the velocity of air at (HERE + 50 m). On the other hand, near the mountain's surface, the velocity of the air might change quickly, so that there are significant differences over just 1 or 2 meters.
In our simulation, we'll keep track of the properties of air in little cubes: density, velocity, temperature, and so forth. How large should we make our cubes?
If each cube is 50 meters on a side,
If each cube is 1 meter on a side,
What should we do? Neither choice is really very good.
But if we create a program which can vary the size of its grid from place to place, depending on the properties of the air, we can achieve the best of both choices.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.