The fourth-order Runge-Kutta method

The Runge-Kutta methods are one group of predictor-corrector methods. The name "Runge-Kutta" can be applied to an infinite variety of specific integration techniques -- including Euler's method -- but we'll focus on just one in particular: a fourth-order scheme which is widely used.

The basic idea of all Runge-Kutta methods is to move from step y_i to y_i+1 by multiplying some estimated slope by a timestep. The difference between particular implementations involve how one estimates the slope. In the fourth-order Runge-Kutta method we will study, the basic idea is to combine 4 preliminary estimates to get one really good slope.

In the diagram below, we start at a location y_i at a time t_i, and we want to figure out the value of y at the time t_i+1. We make 4 estimates of the slope within this time interval. I'll label these estimates with letters k₁ through k₄, as some textbooks do.

k₁ is the slope evaluated at the starting location y_i (black dashed line in figure)

We project this slope forward by HALF a timestep to determine an estimated position (green dot) at this future time

k₂ is the slope evaluated at the location y₁ (green dashed line in figure)

We project this slope forward from the starting point by HALF a timestep to determine an estimated position (brown dot) at this future time

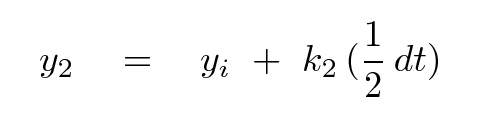
k₃ is the slope evaluated at the location y₂ (brown dashed line in figure)

We project this slope forward from the starting point by a FULL timestep to determine an estimated position (pink dot) at the next timestep

k₄ is the slope evaluated at the location y₃ (pink dashed line in figure)

Once we have these four slopes, we can combine them in a weighted fashion to create an average slope, and use that average slope to compute the next position.