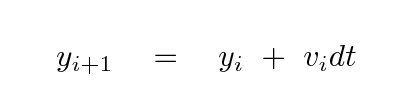
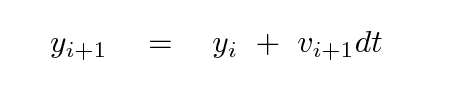
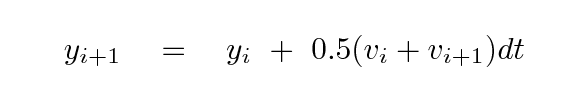
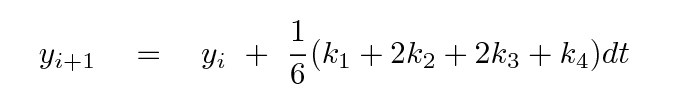
Let's use the "satellite motion around the Earth" project to test the accuracy of several different techniques for computing the motion. We'll include
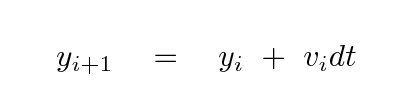
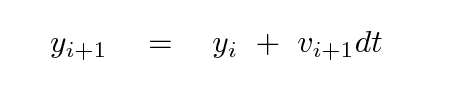
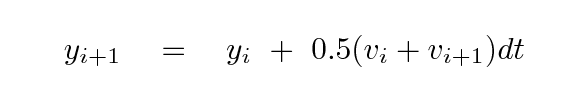
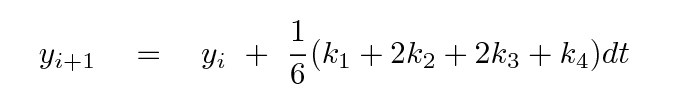
To test these different methods, we'll follow the motion of a satellite around the Earth. We assume a nicely spherical Earth, ignore air resistance and all other complications, and begin with initial conditions:
We'll follow the motion of the satellite for 10 days = 864,000 seconds, which corresponds to roughly 160 orbits. Before we start, we'll compute the satellite's initial total energy E0
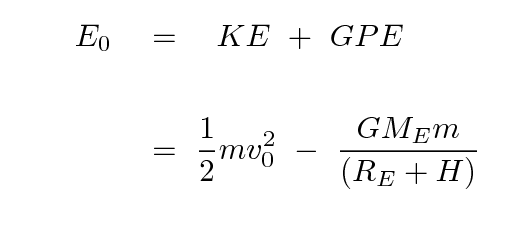
At the end of the simulation, we compute the final total energy Ef. In a perfect simulation, the initial and final energies would be exactly the same. In the actual simulation, they aren't, due to the accumulated errors in each step of the motion. We use the fractional change in total energy f
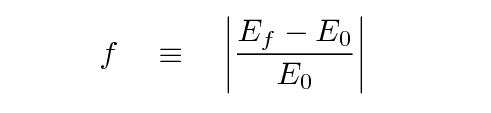
as a metric to describe the quality of the simulation. The smaller f is, the better.
Now, to investigate the properties of each technique, we'll run the simulation many times, using a fixed timestep in each trial. For each technique, we will run trials with timesteps between 0.0001 and 1000 seconds, doubling the timestep each time. So, for example,
Q: How many steps does the first trial take?
Into how many pieces is each orbit broken?
Q: How many steps does the final trial take?
Into how many pieces is each orbit broken?
After running all these simulations (it took about 28 hours on an Intel Pentium 4 3GHz CPU), one can compare the fractional error as a function of timestep.
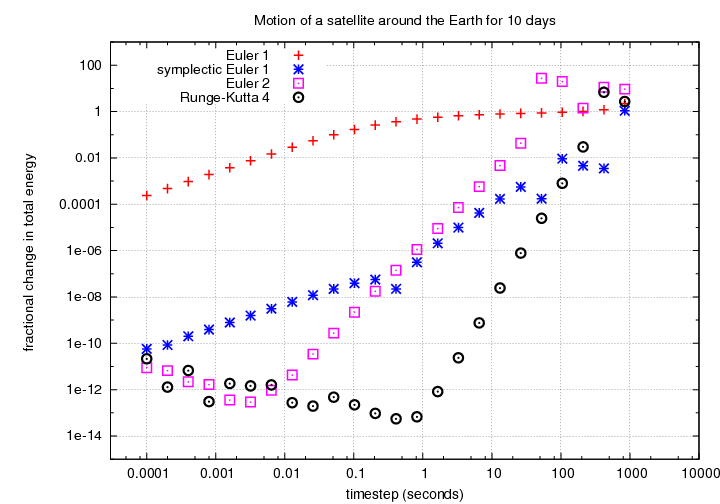
The results have a number of interesting features.
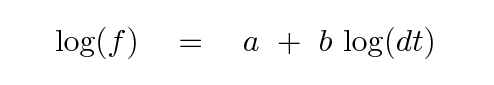
But we can also express the relationship in a more convenient way:
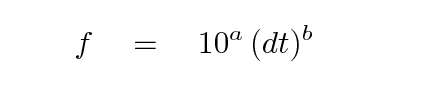
Q: What are the slopes for each technique
over the linear portions of their results?
Q: For each technique, complete the following
statement:
If one cuts the timestep in half,
the technique becomes ______
times as accurate.
When the timesteps are very large, none of the methods works very well. Even though the change in fractional energy may be small, a simulation may not reflect reality. Conservation of energy does not guarantee correct results! Look at the first "orbit" for each technique if we use a timestep of 500 seconds:
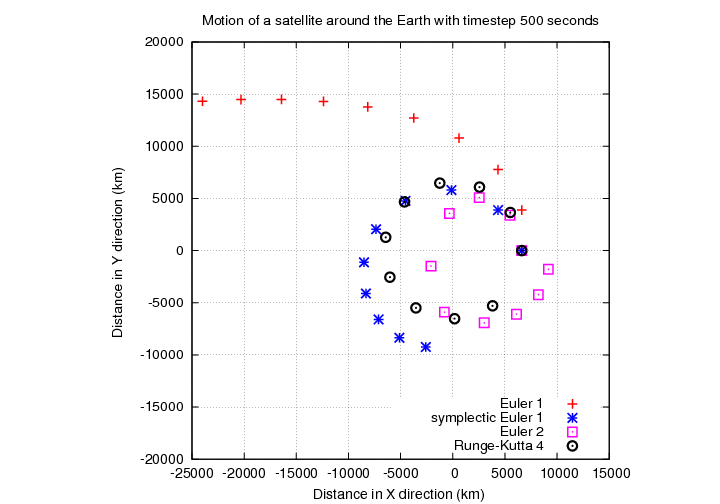
Here's a more detailed view, showing the outline of the Earth.

The symplectic Euler's method had a value of f = 0.1 -- yet it sends the satellite off into a spiral trajectory. The second-order Euler's method claims to have f = 0.04, but it is obviously even worse. The Runge-Kutta method yields f = 0.01, which is almost the same as that for second-order Euler ... but its trajectory is ALMOST a perfect circle.
Don't fall into the trap of trusting the numbers. Always examine results with the Mark I eyeball -- it's an excellent detector of bogus results.