So far, we've restricted ourself to a simple set of boundary conditions: the temperature of each end of a rod (or each edge of a plate) is fixed.
But there are other boundary conditions, too. For example, one end of a rod might be insulated.
Q: What does that mean?
Suppose that the right-hand end of a rod is insulated. That means that no heat can flow out of that end to the right, nor can any heat flow into that end from the right. Any heat flowing into the segment from the left-hand side will be trapped, and simply raise the temperature of the segment.
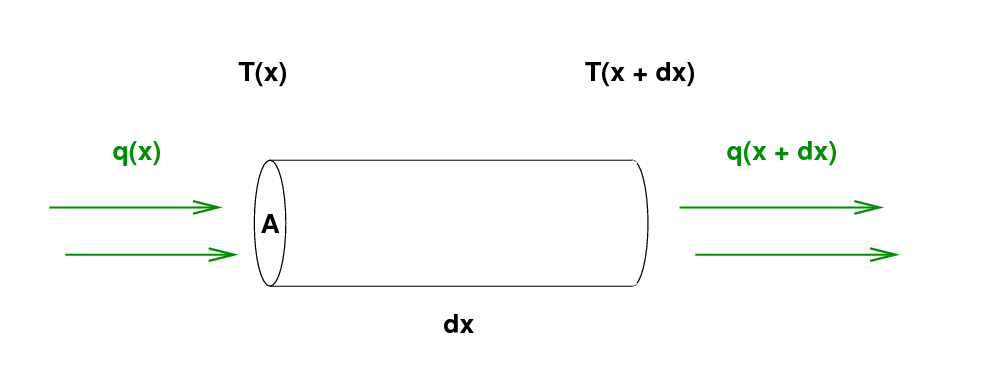
Let's look again at one small section of a metal rod. The section has a width dx and a cross-section area A. We are interested in the amount of heat flowing through this little section of the rod. We'll use the convention that rate at which energy flows through the section, q(x), is positive if the energy flows in the positive X direction. The units of q are
Joules
q = heat flow = -----------
s * m^2

Mathematically,
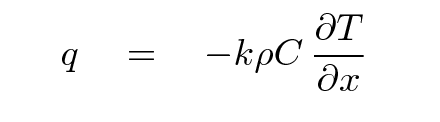
where
q is rate of energy flowing through section
(J / m^2*s)
k is the thermal diffusivity of material
(m^2 / s)
ρ is the density of the material
(kg / m^3)
C is the heat capacity of the material
(J / kg*degC)
T is the temperature of the material
(degC)
x is position
(m)
Note the negative sign: if the temperature increases to the right, then the flow of heat will go to the LEFT.
Another way to write this is in terms of the thermal conductivity of the material:
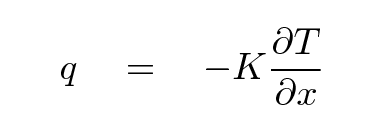
where
q is rate of energy flowing through section
(J / m^2*s)
K is the thermal conductivity of material
(J / s*m*degC)
T is the temperature of the material
(degC)
x is position
(m)
Now, suppose we do know the amount of heat flowing INTO the section from the left end, but no heat can flow OUT of the section from its right end. How does the temperature of the section change as a result?
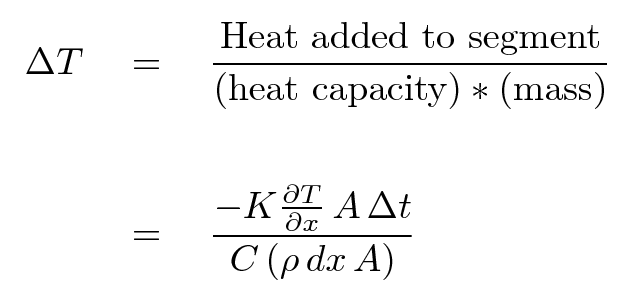
Q: Can you write a simplified expression for the
change in temperature of this segment?
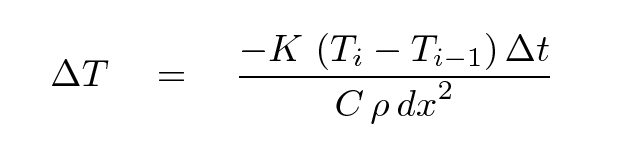
Notice that this does not depend on the cross-section area of the rod: the temperature of a thin rod and a thick rod will change by the same amount in the same period of time.
Q: How can that be? How can a thick rod
change temperature just as fast as a
thin rod?
So, this means that you need to spend some extra time dealing with the very end of a rod if it is insulated. Instead of simply setting its temperature to some fixed value, you need to figure out how much heat is flowing into (or out of) the segment, compute the change in temperature which results, and add that change to the current temperature of the segment.
Suppose that the right-hand end of a rod is not fixed to a source of constant temperature, nor is it insulated; instead, the right-hand end of the rod is free to emit and absorb radiation from its surroundings.
Q: What is the appropriate boundary condition
now?
Q: What do you need to know to compute the
change in temperature of this end of the rod?