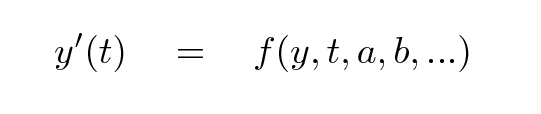
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
What do I mean by a "not-so-simple" situation? I mean one in which the derivative of a function of interest depends in some way on the value of the function itself:
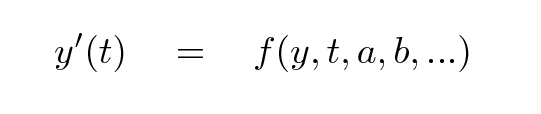
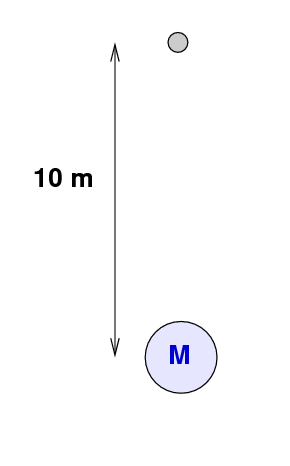 Suppose we have a ball suspended y = 10 m
above a very dense core of neutronium,
which has a mass M = 1012 kg .
We can write down a pair of coupled first-order
differential equations.
Suppose we have a ball suspended y = 10 m
above a very dense core of neutronium,
which has a mass M = 1012 kg .
We can write down a pair of coupled first-order
differential equations.
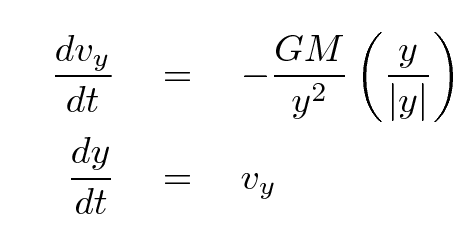
At time t = 0, the ball is motionless ... and then we release it. We have these initial conditions:
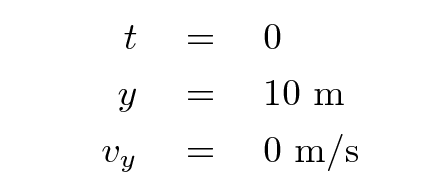
Suppose that we use Euler's method for each of these two differential equations, with a timestep of dt = 1 second. Can you fill in the table below?
time accel vy y (s) (m/s2) (m/s) (m) ------------------------------------------------------ 0 1 2 3 ------------------------------------------------------
Yuck. That wasn't a very good simulation, was it? It's clear that assuming a constant value for the derivative of some quantity over a timestep is a bad approximation; but how can we do any better? We cannot include terms of higher order, since the derivative doesn't have a simple functional form which depends only on time.
The solution is to use an iterative approach: we will predict (poorly) the future value of a quantity, and then use this (poor) future value to estimate a correction to the initial guess. There are many methods which follow this basic predictor-corrector model, but I'll illustrate just one here.
In the example which follows, I'll use the notation that yi is the current value of position and y'i is the current value of its derivative, while yi+1 and y'i+1 are the values of those quantities at the next iteration in time.
First, we predict the future velocity
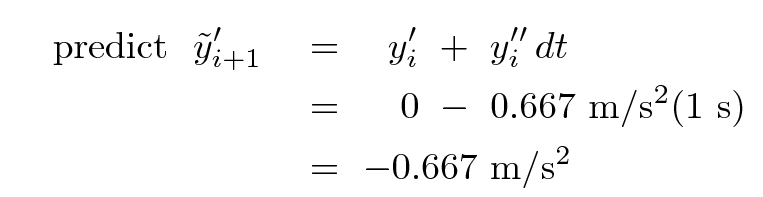
and we predict the future position
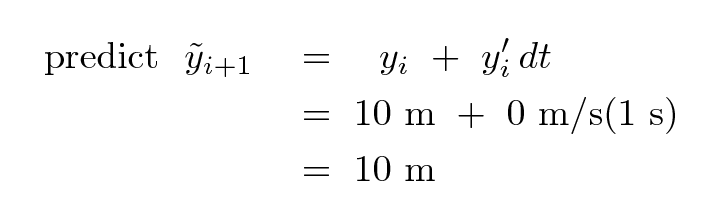
Since we have a guess at the future position, we can now at least guess what the future acceleration will be.
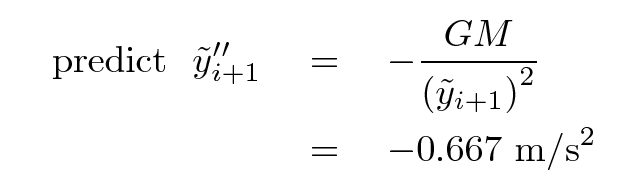
Now, we use those predictions to compute improved versions of the future values; we can make improved calculations because we have at least a rough idea of how the derivatives change with time. So, for velocity, we can now calculate
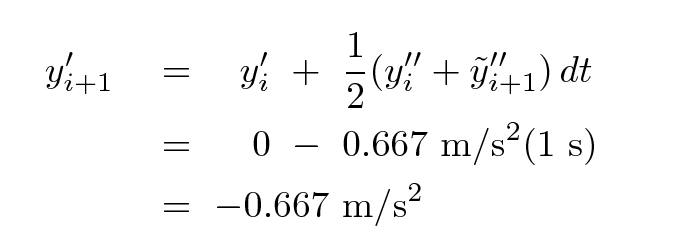
(yes, in this particular case, that really didn't help), and for position,
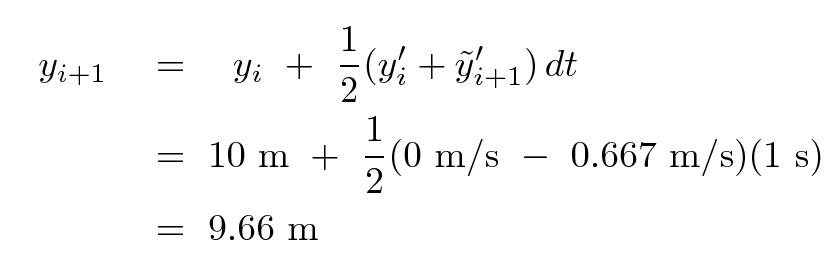
You can see that this method DOES yield a better value for the position after 1 second.
Now, there is nothing to stop us from performing a second iteration: we could use this improved value for the position after 1 second to calculate an even better new acceleration, and then use that better new acceleration together with the initial acceleration to compute a better velocity after one timestep, and so forth. You can decide on your own how many iterations will be best for your situation.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.