 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Last week, we discussed the problem of a ball which is initially thrown upwards from the Earth's surface. The ball's motion was entirely vertical, which meant that the choice of variables in your program was pretty obvious:
y height of ball (m)
v or vy vertical velocity of ball (m/s)
Your next assignment is to follow the motion of a satellite as it flies around the Earth. In the ideal case (uniform spherically symmetric Earth, no other bodies, satellite of negligible mass, etc.), the motion will lie in a single plane. That means that you now need to keep track of a position which has two components, and a velocity which has two components. (When we move on to more complex situations, you will have 3-dimensional quantities, of course).
Q: How CAN you represent two-dimensional
position and velocity in your code?
Q: How SHOULD you?
Well, one choice is to follow the practice we follow in the University Physics sequence, and in other courses, too, when we solve problems with a pencil and paper:
x is the position in x-direction (m) y is the position in y-direction (m) vx is the velocity in x-direction (m/s) vy is the velocity in y-direction (m/s)
This method has the advantage that it's very easy to understand, for some person who wasn't involved in the program design. For example, if a student taking this course five years from now finds a copy of a program written in this way, he will probably be able to figure out right away what the satellite's starting position is.
On the other hand, because we are using two separate variables for the two components of position, it means that we will need to have two separate lines of code to undate each position: something like this:
% update the position for the next timestep x_new = x + vx*dt; y_new = y + vy*dt;
That may look trivial, and it is, if we use a simple first-order Euler's method. But what if we are using a fourth-order Runge-Kutta method? Then each calculation grows more complex ...
% update the position for the next timestep x_new = x + (k1x + 2*k2x + 2*k3x + k4x)*(dt/6.0); y_new = y + (k1y + 2*k2y + 2*k3x + k4y)*(dt/6.0);
(Yes, there _is_ a mistake in the lines above. Can you find it? When you write very similar lines of code, copying one line and then modifying a bit of it, little mistakes like this happen frequently)
Another method for dealing with multi-dimensional situations is to define vectors or arrays for each quantity, and then loop over the indices to carry out calculations for each dimension. For example,
for (i = 1 : 2) x_new(i) = x(i) + v(i)*dt; end
The advantage of this approach is that you only need to write each long line of code -- or each chunk of several lines of code -- once, not twice for a 2-D problem or three times for a 3-D problem. The disadvantage is that it might be harder for someone else to understand exactly what's happening (especially if that someone is accustomed to programming languages which use 0-index arrays instead of 1-index arrays).
You can see a good deal of on-line documentation for MATLAB's way of dealing with vectors by typing
help elmatin the Command Window.
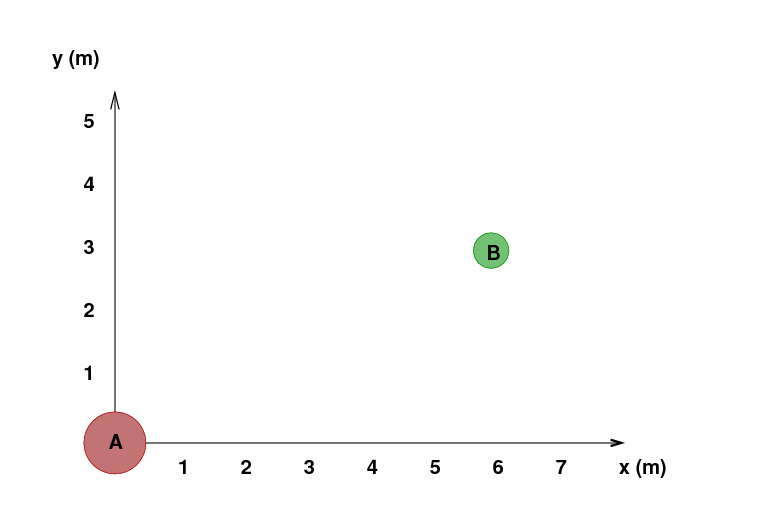
Suppose there are two bodies isolated in space:

What is the gravitational force on body B due to the more massive body A?
Q: Write down the magnitude of the force on B
due to A.
Q: Write down the x- and y-components of the force
on B due to A.
How did you break the total force into its x- and y-components? Did you use the trigonometric functions sin and/or cos? If so, what was the angle given to those functions? How did you define the angle?
It turns out that there's a method for computing components of the gravitational force which doesn't require the trig functions; since those functions may take a computer some time to calculate, avoiding them can speed up the results.
Q: How can you compute the x- and y-components of
this gravitational force without using
trig functions?
Q: Assume that a MATLAB program has
quantities stored in the following variables
G universal const of gravitation (N*m^2/kg^2)
mA mass of A (kg)
xA position of A in the x-dir (m)
yA position of A in the y-dir (m)
mB mass of B (kg)
xB position of B in the x-dir (m)
yB position of B in the y-dir (m)
Write down on paper MATLAB code which would
compute both x- and y-components of the force on
body B due to body A.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.