Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
There are a number of factors which affect the quality of photometry of star in a CCD image. One is the exposure time: the longer the exposure time, the higher the signal in a star, and so the more precise the measurements. Of course, if one exposures too long, one will saturate the CCD, which ruins the measurements. But how long an exposure time is necessary?
The answer depends on your goal. If you simply want to verify that an object is present at a particular location, you may accept a very faint, barely noticeable dot of light. If you want to measure the position of an asteroid to an arcsecond, you would need a little more signal. If you want to make a very rough estimate of magnitude, to ten percent, say, then you might need more signal. And if the goal is to look for tiny variations in light of a variable star, you might need to expose long enough that the star comes close to the non-linear regime.
So how can you figure out the appropriate exposure time for a given project? There are two approaches:
You can do exactly the same thing with your astronomical observing: take a series of images with increasing exposure times, and measure the object of interest on each one. The shortest exposure which provides enough precision for your goal is the right length.
This actually isn't a bad idea if you have huge amounts of observing time. On the other hand, if you are given just a single night on a big telescope, you probably won't want to waste any time taking a series of pictures, most of which turn out to be useless.
1
fractional uncertainty = -----
S/N
So, for example, if the S/N ratio is 50, the photometry will
have an uncertainty of 0.02, which is the same as 2 percent,
and which is approximately 0.02 magnitudes.
Your job is to figure out the appropriate cash reserves for McKing restaurants -- the amount of money which should be kept in the registers. You decide it is important to know the answer to the question
How many customers each hour pay with a $20 bill?
So, you do a little research. You go to a local store in Henrietta and count the number of customers who need change for a $20. You find
Hour-by-hour counts throughout the day
Day 1: 11 12 9 12 9 7 14 14 12 8
Day 2: 7 10 12 5 9 14 10 11 8 7
Day 3: 10 5 9 6 17 10 12 6 16 8
A more convenient way of displaying this information is in the form of a histogram.
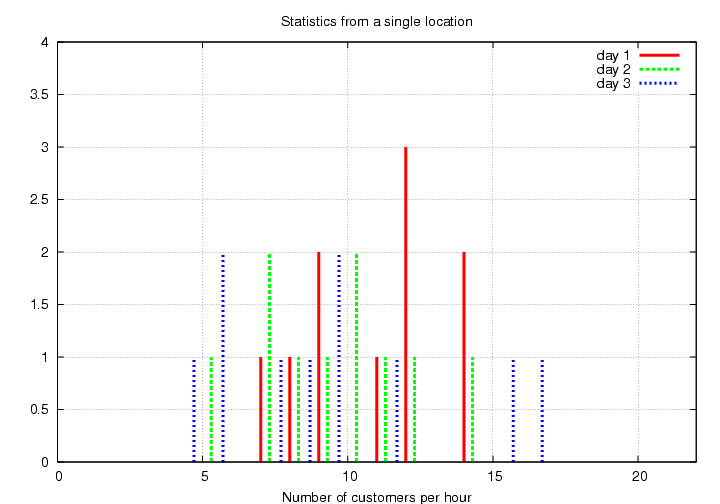
There seems to be quite a bit of variation from day to day. So you extend your period of study over 10 days, then 100 days, and take the average numbers during each period.
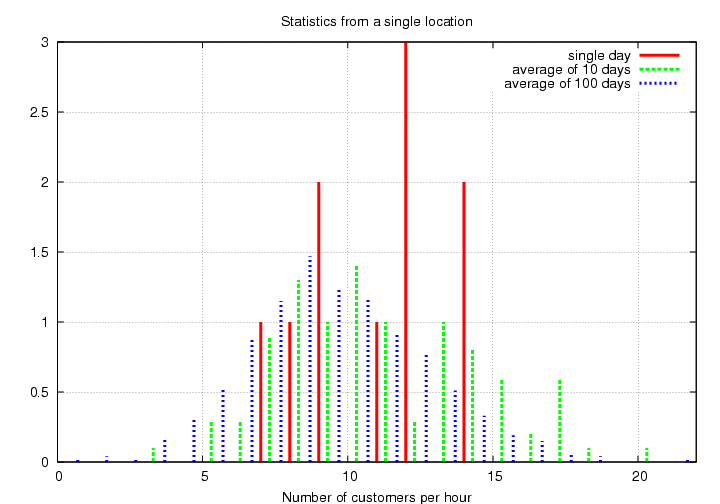
Hmmm. The distribution becomes smoother and more symmetric with more time, doesn't it? If you were to watch the same store for 3 years, you might get a distribution like this:
Exercise:
- What is the mean value of this distribution?
The standard deviation is (I measured it myself) about 3.1 customers per hour. That is, the scatter around the mean value is about +/- 3 customers.
- What fraction of the mean value is the scatter? That is, by what percent of the average number of customers per hour does the measurement fluctuate?
Now, you want to get a better idea for this value, because it turns out to be crucial for figuring out how much cash you need to keep in the store. So, instead of looking at a single store, you decide to hire people to make similar counts at all the restaurants in Monroe County. There are N = 100 restaurants, so you will find a much larger number of customers per hour -- at all stores -- who pay with $20 bills.
Here are the raw counts for the first few days of your big study.
Hour-by-hour counts throughout the day
Day 1: 1023 945 1004 984 1024 990 1023 1036 980 1022
Day 2: 1061 1041 1004 1006 977 1037 1069 1004 987 969
Day 3: 953 992 970 1041 1020 1016 984 978 948 995
Again, you decide to use a histogram to display this information.
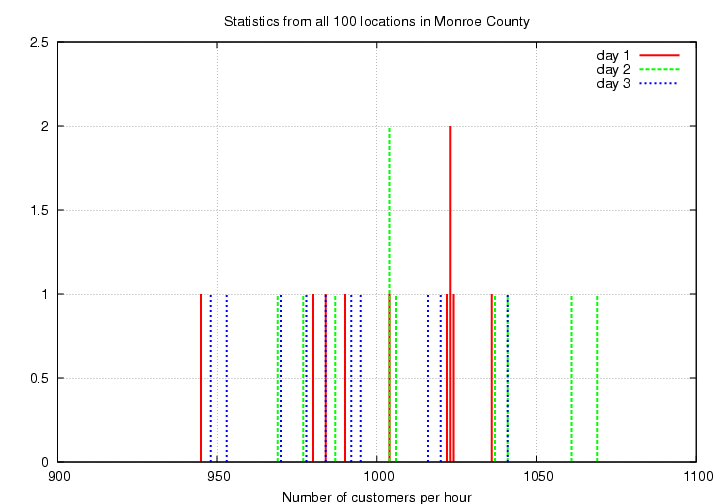
To diminish the fluctuations, you again extend your period of study over 10 days, then 100 days, and take the average numbers during each period.
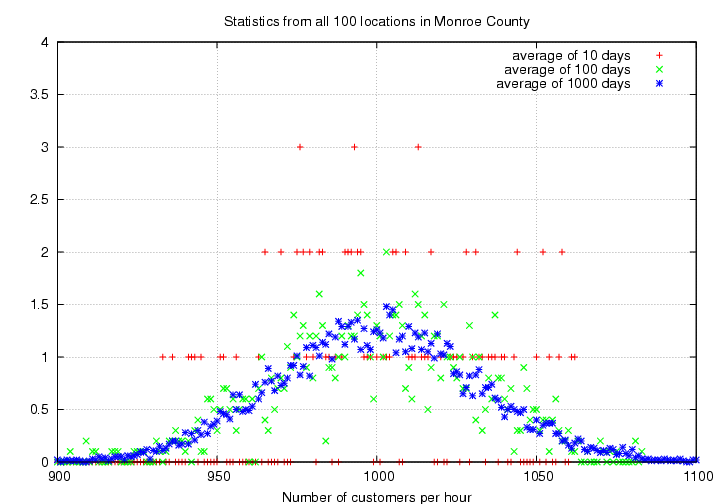
Once again, the distribution becomes much smoother and symmetric when you average over a long period.
Exercise:
- What is the mean value of this distribution?
The standard deviation is (I again measured it) about 32 customers per hour. That is, the scatter around the mean value is about +/- 32 customers.
- How does this scatter around the mean value compare to the scatter around the mean for a single location? Use the raw numbers of customers to make the comparison.
- Now, do the comparison again, but this time, use the fractional scatter. That is, by what percent of the average number of customers per hour does this county-wide measurement fluctuate? How does that percentage compare to the percentage scatter for a single store?
One more time --- you still need better statistics. So, you now hire people to make similar counts at all the restaurants in the entire Northeastern United States. There are N = 10,000 restaurants, so you will find a much, much larger number of customers per hour -- at all stores -- who pay with $20 bills.
Here are the raw counts for the first few days of your giant study.
Hour-by-hour counts throughout the day
Day 1: 100115 99460 100171 100405 100621 100448 99654 99792 99892 100109
Day 2: 100070 99780 100246 100124 99561 99764 100100 100669 100008 100209
Day 3: 100007 99265 99960 100080 100309 100364 100183 99897 101023 99771
Again, you decide to use a histogram to display this information. And again, you extend your period of study over 10 days, then 100 days, and take the average numbers during each period.
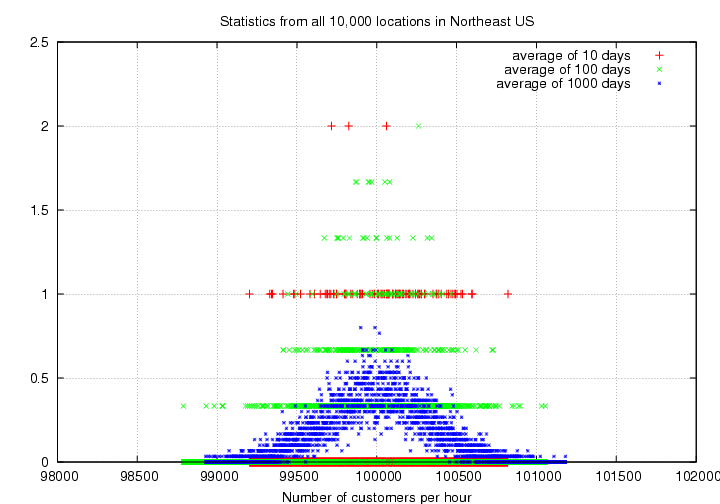
Exercise:
- What is the mean value of this distribution?
The standard deviation is this time about 318 customers per hour. That is, the scatter around the mean value is about +/- 318 customers.
- How does this scatter around the mean value compare to the scatter around the mean for a single location, or for N=100 locations? Use the raw numbers of customers to make the comparison.
- Now, do the comparison again, but this time, use the fractional scatter. That is, by what percent of the average number of customers per hour does this nation-wide measurement fluctuate? How does that percentage compare to the percentage scatter for a single store, or for N=100 stores?
The bottom line is that when you compute the statistics of random events which occur at some average rate, you can make a much more precise measurement -- in fractional terms -- when you observe a large number of events. The smaller the number of observed events, the larger (in fractional terms) the signal will fluctuate around its mean value.
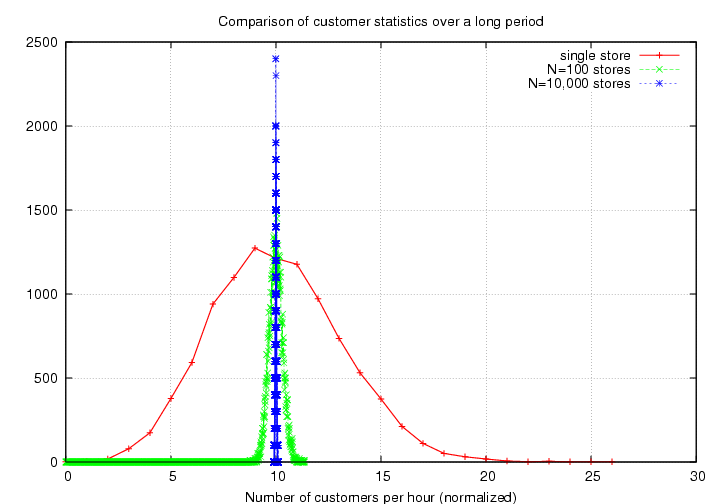
So, even though the absolute size of the fluctuations (or "noise") increases with signal strength, the fractional size of the noise decreases with signal strength.
typical fluctuation
fractional noise = ---------------------
mean value
We can also express this idea in another way by taking the inverse of this fraction: we call that the signal-to-noise ratio
mean value
Signal-to-noise S/N = ---------------------
typical fluctuation
mean value
= ---------------------
standard deviation
When the S/N is high, we can make a very precise measurement; but when the S/N is low, we can only make a rough measurement.
We'll see how this statistical property affects our ability to measure the brightness of a star or galaxy in our next class meeting. In the meantime, the
performs a somewhat more complicated version of these same calculations to help you estimate the S/N ratio for a typical astronomical exposure. For planning purposes, you might estimate
S/N = 1 to 5 barely detected
= 5 to 50 fairly good measurement
= 50 to 500 high quality measurement
Exercise:
- Use the on-line signal-to-noise calculator to estimate the exposure time required to reach a signal-to-noise ratio of 100 for a star of magnitude 15 in the V-band, using our 12-inch telescope and our ST-8 CCD camera. You can use these values for the camera on that telescope:
- pixel size 1.85 arcseconds
- FWHM = 4 arcseconds
- readout noise = 15 electrons
- aperture size = 6 arcseconds
- Use the on-line signal-to-noise calculator to find the exposure time required to make a measurement with a precision of 10 percent (about 0.10 magnitudes) of a star of magnitude 18, using the ST-8 camera on the 12-inch telescope and no filter.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.