Readout Noise, and Total Noise

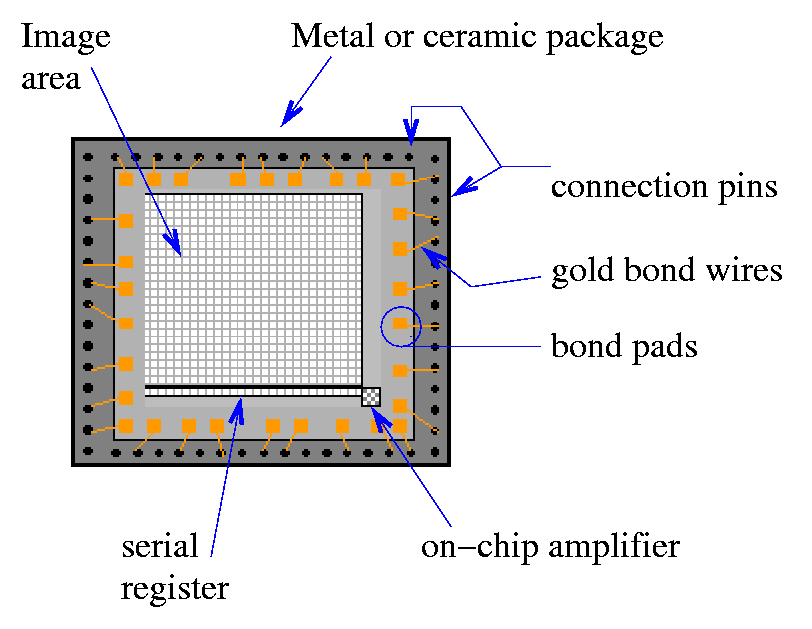
There's one more source of noise inherent in all CCDs, which is especially important for images with short exposures and/or very faint background levels. This is the readout noise, sometimes abbreviated "readnoise".

It is a consequence of the imperfect operation of physical electronic devices. Recall the order of operations the CCD performs to turn the electrons knocked free by photons in every pixel into a signal which can be read by a computer:

Electrons transferred to "amplifier"; really a capacitor. Units are coulombs.
The voltage induced by this charge is measured. Units are volts.
An Analog-To-Digital (A/D) unit converts the voltage into some other voltage, which may have only one of several discrete levels. Units are still volts.
The voltage is converted into a number which is passed from the hardware to the computer software as the pixel's value. Units are counts, also called "Data Numbers" (DN) or "Analog-to-Digital Units" (ADUs).

Readout noise occurs in step 2: the measurement of a very small packet of charge by the readout amplifier.

The amplifier can't do a perfect job of measuring the charge in the clump of electrons. Typically, it gives the right value on average, but with some random scatter. "Readout noise" is simply a measure of this scatter around the true value. People usually quote its value in electrons, because, after all, the packet of charge is made up of electrons.

Measuring the readout noise

How can we determine this value? A simple -- but approximate way -- is to look at a frame which ought to have the same pixel value everywhere. Suppose that we could magically illuminate the CCD with, say, exactly 100 photons in every pixel. All pixel values ought to be identical, so any differences between pixels might be blamed on random fluctuations in the readout amplifier.

Why isn't this a practical method?

Okay, so uniform illumination isn't very practical. How about uniform darkness instead? If we take a dark frame of zero exposure time (sometimes called "zero frames", sometimes called "bias frames"), then there will be

no photons hitting the chip
no time for thermal motion to knock electrons free (well, not much time, anyway)

In theory, in an ideal world, two such "zero frames" ought to be identical. If we subtract one from the other, we ought to get exactly zero counts, everywhere. Try it!

Pick two of the zero-second dark frames. If someone is sitting nearby, talk with him to make sure that the two of you pick a different pair.
Make copies of these two frames, called copyA.fit and copyB.fit.
Subtract copyB.fit from copyA.fit
Calculate the mean and standard deviation (rms) of the difference image
Is the mean zero? It ought to be close
Is the standard deviation zero?

The standard deviation of this difference image is a result of random scatter in the first image copyA.fit AND random scatter in the second image copyB.fit. In order to find the standard deviation in a single zero frame, we need to divide the stdev of the difference image by the square root of two:

                                stdev of diff image
      stdev of one image   =   ---------------------
                                    sqrt(2)

This yields the readout noise of the CCD in units of counts. What we really want to know is the readout noise in electrons.

Convert your value of readnoise from counts to electrons, using the class average value for gain from yesterday.
Compare your result to that of someone(s) sitting nearby.
Compare your result to the manufacturer's value

The main sources of noise in CCD measurements

Okay, so now you know about the three main sources of random scatter in CCD pixel values:

Readout noise: Present in all images, same amount regardless of exposure time
Thermal noise: Increases with time: the scatter is equal to the square root of the number of THERMAL-electrons knocked free in each pixel. Can be cut down by lowering the temperature of the chip.
Photon noise: Depends on the amount of light hitting the chip. The scatter is equal to the square root of the number of PHOTO-electrons knocked free in each pixel. Can come from background sky light, or from photons from the target object.

We can put these sources together into a single equation to calculate the overall uncertainty in the number of electrons in a single pixel:

         variance (electrons)  =    (readout noise)*(readout noise)  +
                                    (number of thermal-electrons)    +
                                    (number of photo-electrons)

Or, in terms of the standard deviation we can expect to see in repeated measurements,

         stdev (electrons)     =   sqrt (variance)

                               =   sqrt [ (readout noise*readout noise) +
                                          (number of thermal-electrons) +
                                          (number of photo-electrons) ]

People often abbreviate these quantities like so:

         R     =     readout noise (sqrt of number of electrons)

         D     =     "dark current", number of thermal electrons 

         P     =     total number of photo-electrons knocked free

In which case the equation for stdev, in electrons, becomes


          stdev (electrons)    =  sqrt (  R*R  +  D  +  P )

Notice that the readnoise noise R term is squared, simply because people have customarily used the standard deviation of the readnoise as the quoted quantity, rather than the number of readout electrons themselves.

Exercises

You take a zero-second dark frame at camera temperature of +23 degrees Celsius. Assume that the readout noise doesn't vary much with temperature, so you can use today's measurements (from a set of cold frames) to estimate the readout noise. What will be the standard deviation per pixel, in electrons?
What will be the standard deviation per pixel, in counts?
Now you take a 10-second dark frame at the same warm temperature. Estimate the standard deviation per pixel in electrons. (You may want to pull out the graph you made last week showing mean pixel values for warm dark exposures.)
Ditto, in counts.
You take a 100-second dark frame at the same warm temperature. Estimate the standard deviation per pixel in electrons.
Ditto, in counts.
Which source of noise dominates the short exposures? Which source of noise dominates the long exposures?