Right Ascension and Declination
On Earth, one way to describe a location is with a coordinate system which is fixed to the Earth's surface.
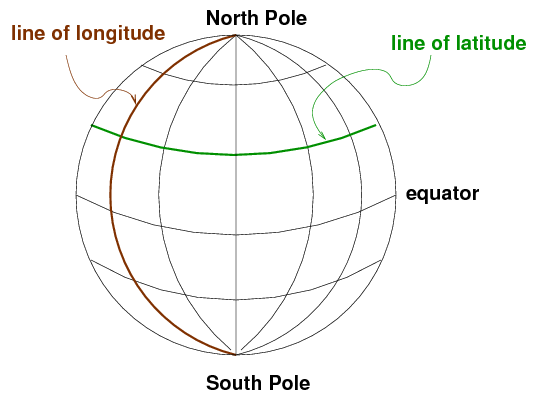
The system is oriented by the spin axis of the Earth, and has special points at the North and South Poles. We use lines of latitude and longitude to demarcate the surface. It's obvious that latitude is measured away from the equator. But where is the starting point for longitude? There is no "obvious" choice. After a lot of dickering, European nations finally decided to use the location of the Greenwich Observatory in England as the starting point for longitude.
There are several ways to specify a location -- for example, that of the RIT Observatory. One can use degrees:
latitude 43.0758 degrees North, longitude 77.6647 degrees West of Greenwich
Or degrees, minutes and seconds:
latitude 43:04:33 North, longitude 77:39:53 West
Or, in the case of longitude, one can measure in time zones. The sun will set at the RIT Observatory about 5 hours and 11 minutes later than it does at Greenwich, so one could say
latitude 43:04:33 North, longitude 05 hours 11 minutes West
The celestial coordinates
On can make a similar coordinate system which is "fixed to the sky":
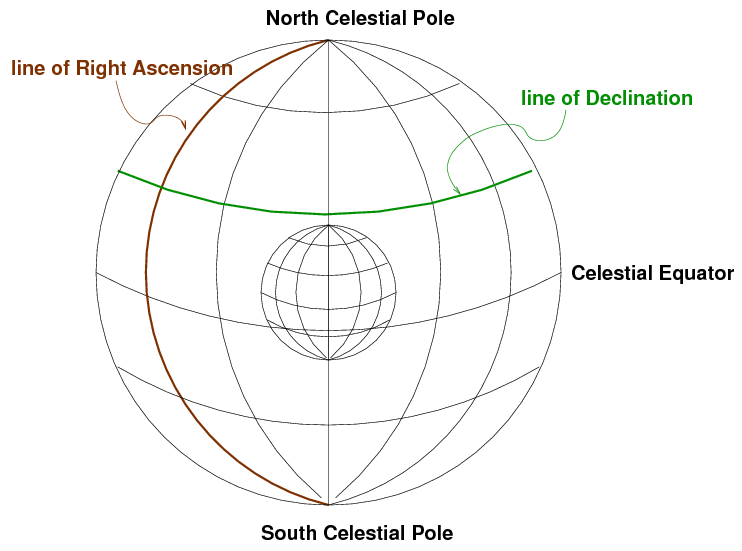
Once again, we use the Earth's rotation axis to orient the coordinates. There are two special places, the North and South Celestial Poles. As the Earth rotates (to the East), the celestial sphere appears to rotate (to the West). Stars appear to move in circles: small ones near the celestial poles, and large ones close to the celestial equator:

Image copyright
David Malin.
We again use two orthogonal coordinates to describe a position:
- Declination, like a celestial latitude
- Right Ascension, like a celestial longitude
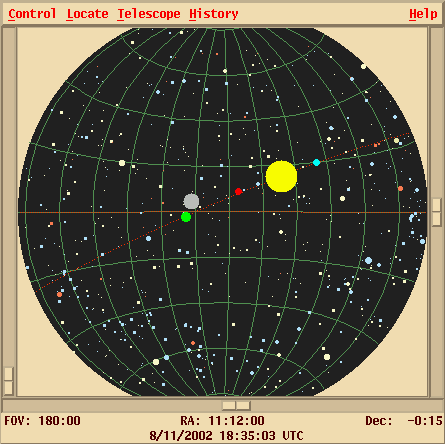
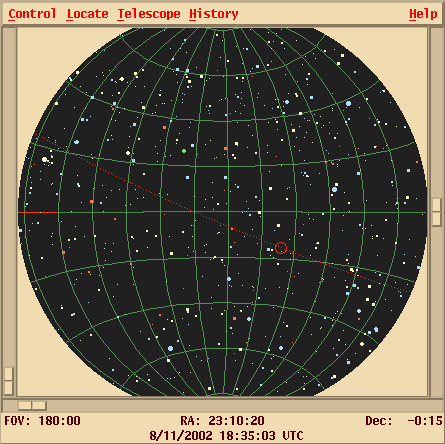
Once again, there are several ways to express a location. The star Sirius, for example, can be described as at
Right Ascension 101.287 degrees, Declination -16.716 degrees
We can also express the Declination in Degrees:ArcMinutes:ArcSeconds, just as we do for latitude; and, as usual, there are 360 degrees around a full circle. For Right Ascension, astronomers always use the convention of Hours:Minutes:Seconds. There are 24 hours of RA around a circle in the sky, because it takes 24 hours for the Sun to move all the way from sunrise to the next sunrise.
Right Ascension 06:45:09, Declination -16:42:58meaning
- the Right Ascension is 6 hours, 45 minutes, 09 seconds
- the Declination is -16 degrees, 42 arcminutes, 58 arcseconds
What's the difference between an "arcminute" and a "minute"?
- one degree is divided into 60 arcminutes
- one arcminutes is divided into 60 arcseconds. Therefore, there are 3600 arcseconds in one degree
- one hour of time is divided into 60 minutes of time
- one minutes of time is divided into 60 seconds of time. Therefore, there are 3600 seconds of time in one hour of time
Exercises
- How many degrees are there all the way around the celestial equator? How many hours are there around the celestial equator?
- How many degrees make up one hour of Right Ascension?
- How many degrees are there in one minute of Right Ascension?
- How many arcminutes are there in one minute of Right Ascension?
- How many arcseconds are there in one second of Right Ascension?
These two angles specify uniquely the direction of
any object in the sky.
Some telescopes have
alt-az mounts
which swivel in these two perpendicular axes;
camera tripods and tank turrets are other examples
of alt-az devices.
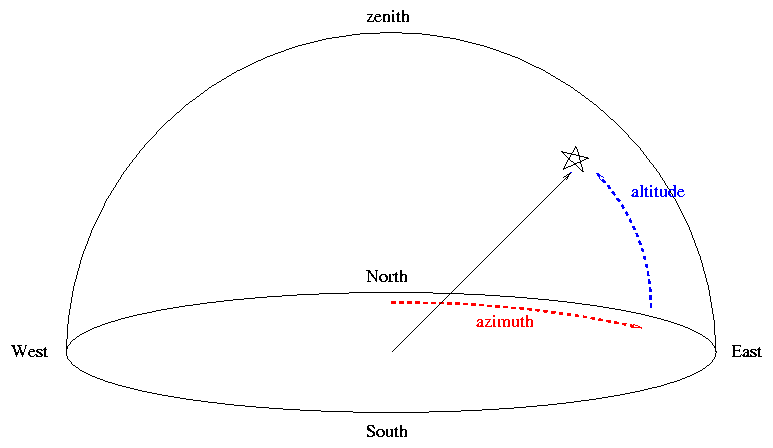
The altitude of an object is especially important from
an practical point of view:
any object which has an altitude less than zero is below
the horizon, and hence inaccessible.
Moreover, the altitude of an object is related to its
airmass,
a measure of how much air the light from that object
must traverse to reach the observer.
The larger the airmass, the more light is scattered or
absorbed by the atmosphere, and hence the fainter an
object will appear.
We'll deal with airmass at greater length a bit later.
However, note that two observers at different locations on Earth
will not agree on the (alt, az) position of an object.
Moreover, as the Earth rotates, an object in the sky appears to
move from East to West,
so its (alt, az) position changes from moment to moment.
It is possible to convert from (RA, Dec) to (alt, az), or vice versa.
One needs to know two factors:
In these modern times, it's usually easiest to use one
of the many fine planetarium programs on a computer to
do this work.
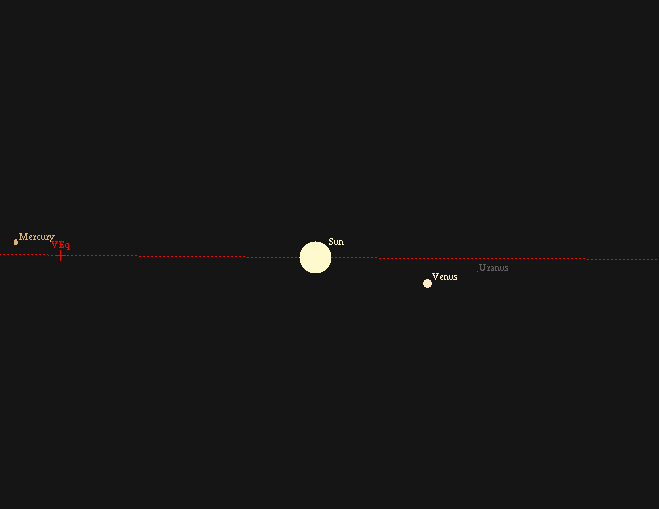
The ecliptic coordinate system is convenient when
dealing with objects in the solar system:
they are concentrated towards the ecliptic equator:
If you zoom in, you can see that the major planets
lie slightly above or below the ecliptic equator,
because their orbits around the Sun are inclined
slightly with respect to the Earth's.
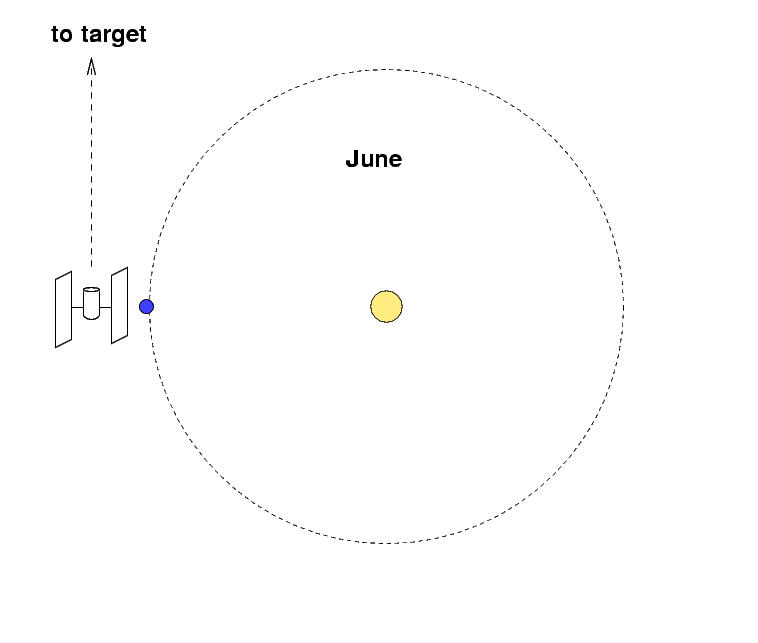
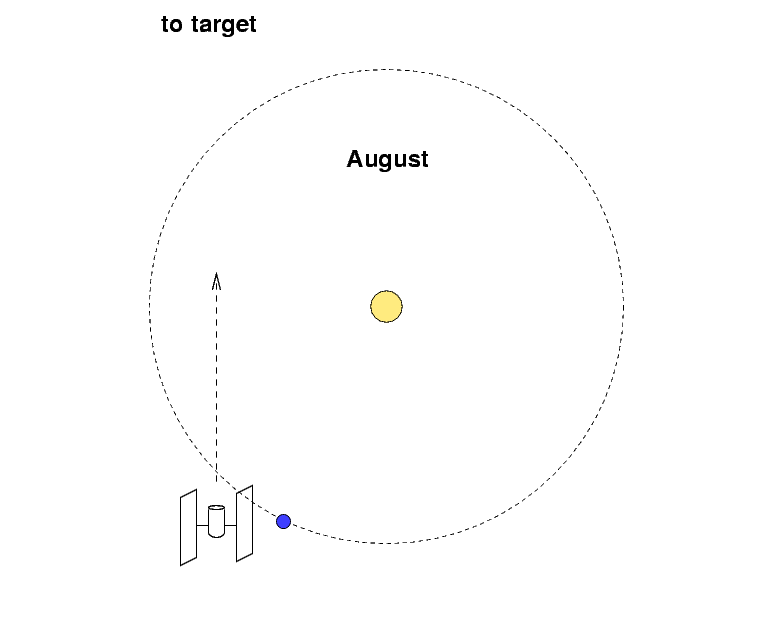
Ecliptic coordinates can also be important when you
want to avoid the solar system.
Telescopes in space, such as the Hubble Space Telescope
or the Chandra X-ray Telescope,
cannot point close to the Sun
(or else they might suffer damage to their detectors).
For some purposes, astronomers want to make very,
very long exposures: days or even weeks long.
During such a long exposure, the Earth may move a
significant fraction of its entire orbit,
which can cause a target originally far from the Sun ....
... to move closer to the Sun, from the telescope's point
of view.
Therefore, astronomers sometimes choose their
very deep fields
On a warm July evening in Rochester, the Milky Way
stretches overhead, with the galactic center
just above the southern horizon.
If you make a map of the sky in galactic coordinates,
the Milky Way runs right across the middle.
The section we see in the summer sky from Rochest is
in mostly the left half of this map.
An infrared map of the sky in galactic coordinates
made by the COBE satellite is dominated by emission
from dust in the Milky Way,
but also shows a faint band of light
due to emission by dust particles in the
solar system.
Note that the plane of the solar system is tilted by almost
ninety degrees relative to the plane of the Milky Way.
Last modified by MWR 3/6/2005
Altitude and Azimuth
These two coordinates,
altitude (or "alt")
and
azimuth (or "az"),
are centered on the observer.
Exercises
The calculations involve some spherical trigonometry.
One can find the details in any good book on celestial mathematics,
such as
Ecliptic (Solar System) coordinates
For objects within our solar system --
planets, asteroids, comets --
it often helps to use a coordinate system
centered on the Sun, with its equator running along
the plane of the planetary orbits.
We call this the ecliptic coordinate system.


Galactic Coordinates
One more set of coordinates comes into play
if one studies the distribution of stars
within our Milky Way Galaxy,
or the distribution of other galaxies
in the far reaches of space.
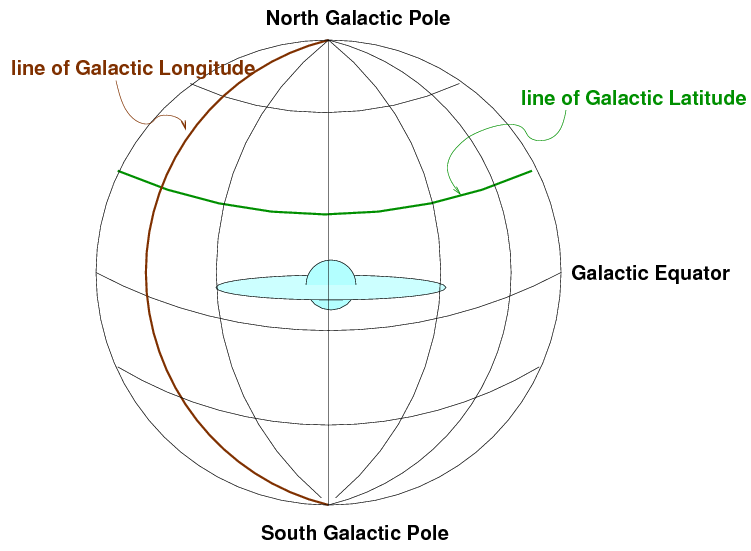
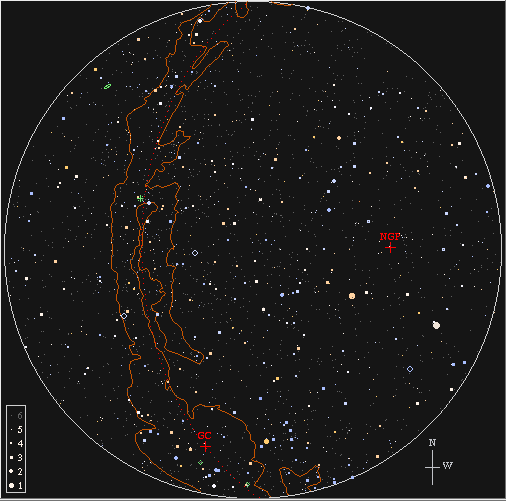

Map courtesy of the
Lund Observatory

Homework
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.