
Image copyright Tony and Daphne Hallas , provided by Astronomy picture of the day
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The answer seems to be obvious: a collection of galaxies within some relatively small volume. And, indeed, when we look at the distribution of galaxies in space on large scales, we find that they do indeed tend to appear in clumps.

Image copyright
Tony and Daphne Hallas , provided by
Astronomy picture of the day
The clustering tendency is obvious if one makes a map of the distribution of galaxies in space.
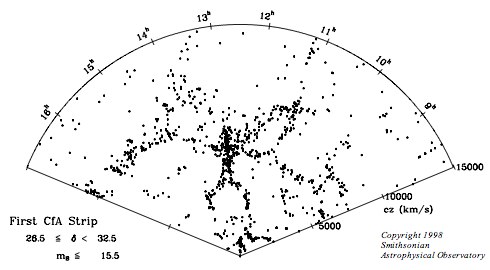
Image courtesy of
The Galaxy Zoo Blog
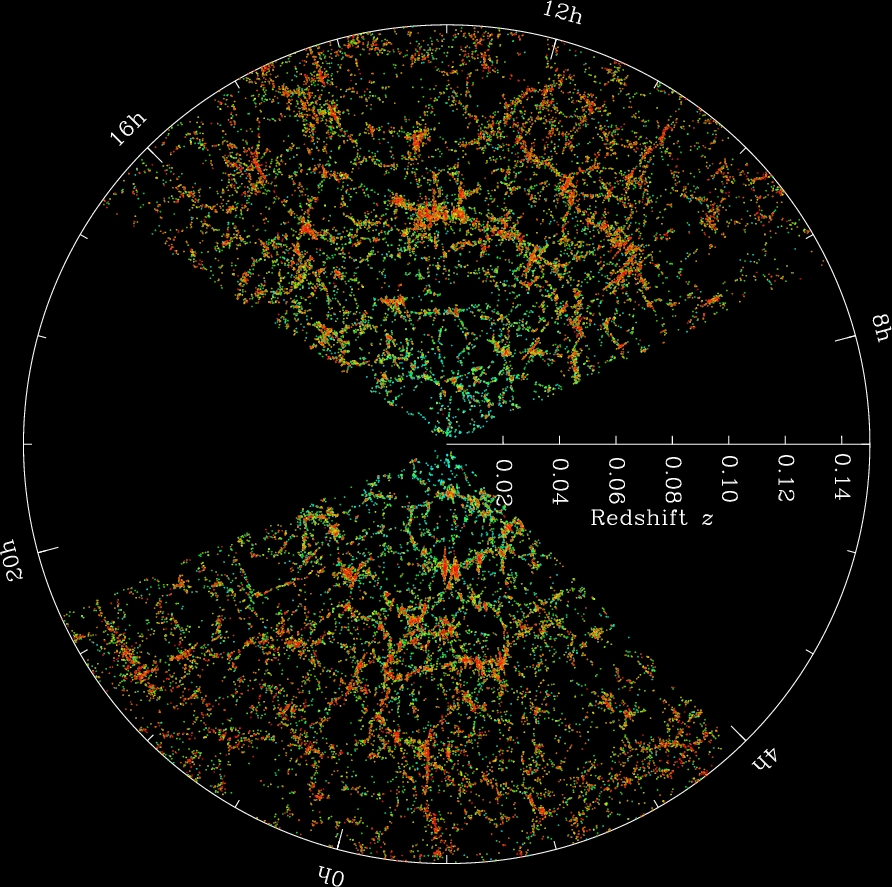
Image courtesy of
The Sloan Digital Sky Survey
One of the most frequently used catalogs of galaxies is known as the Abell catalog , so let's look at a few of the terms used in it to describe galaxies. The original catalog was described in Corwin, ApJS 3, 211 (1958), but successive papers have increased its scope. The most recent paper in a series is Abell, Corwin and Olowin, ApJS 70, 1 (1989)
Number of galaxies Richness class
-------------------------------------------
30 - 49 0
50 - 79 1
80 - 129 2
130 - 199 3
200 - 299 4
300 - 5
-------------------------------------------
Mag of tenth-brightest Distance group
-------------------------------------------
13.3 - 14.0 1
14.1 - 14.8 2
14.9 - 15.6 3
15.7 - 16.4 4
16.5 - 17.2 5
16.3 - 18.0 6
18.1 - 7
-------------------------------------------
Modern galaxy catalogs are defined, not by visual scanning of plates, but by criteria used by a computer to sift through thousands and millions of objects in a big database. Modern catalogs may also use redshift or color information to judge whether galaxies in some particular region of the sky are actually at a common distance. Finally, some modern catalogs are based on observations made at wavelengths outside the optical.
When lots of galaxies come together in a small volume, there are a number of ways that they can interact. One way to divide these interactions is by computing the timescales for various processes.
Q: A typical cluster has a size
(radius or diameter, who cares?)
of around 1 Mpc.
A typical galaxy in a rich cluster
has a velocity of order 1000 km/s.
What is the crossing time for a typical
rich cluster? How does that compare
to the age of the universe?
The crossing time is an appropriate scale for the time over which an initial big cloud of galaxies/proto-galaxies might collapse into a bound cluster. Under certain conditions, the objects in such a collapse will undergo violent relaxation, which means that their dynamical properties will move into some semblance of equilibrium.
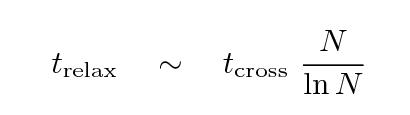
Q: A typical rich cluster has of order
N = 1000 members.
What is the two-body relaxation time for
a typical rich cluster? How does that compare
to the age of the universe?
As a result, we don't expect to see clusters to show mass segregation, in which the more massive galaxies have all sunk to the central regions, while the low-mass galaxies are flying out to large radii. Globular clusters, on the other hand, do show this sort of segregation because their two-body relaxation times are much shorter.
Some other terms that you may see in connection with clusters are
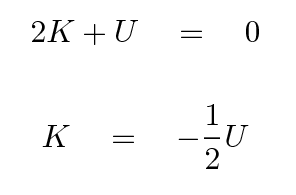
Now, most of the galaxies in a cluster are certainly not moving in circular orbits. That means that the connection between kinetic energy and gravitational potential energy isn't quite so easy to express as it is for, say, gas in the disk of the Milky Way. Nonetheless, it's clear that the mass of the cluster must be given by some equation of the form
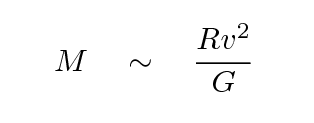
Q: The Virgo cluster is rather lumpy, but
the velocity dispersion is something
like 700 km/s.
The radius of the cluster is again hard
to define, but something like
3 degrees, and the distance
is roughly 18 Mpc.
Estimate the mass of the Virgo cluster.
This sort of calculation was first published by Fritz Zwicky back in 1933; he used the Coma Cluster in his example, deriving a mass of M > 9 x 1046 grams for the cluster. While the measurements of radial velocity available to him at the time were fine, the distance to the cluster was underestimated by a large factor, so his mass is likewise smaller than the value we currently derive.
If we measure the light from the visible galaxies in the cluster, we can compute a mass-to-light ratio for the cluster as a whole.
Binggeli, Tamman and Sandage (AJ 94, 251, 1987)
measure a luminosity of roughly
L(B) = 120 x 1010 solar
in the B-band for galaxies within 3 degrees
of the center of the Virgo Cluster.
Q: What is the mass-to-light ratio in blue light
for the Virgo Cluster?
Zwicky performed this sort of calculation back in the 1930s and found a mass-to-light ratio of 500 for the Coma Cluster. He pointed out that this was quite a puzzle, but the astronomical community in general didn't pay much attention to it.
More sophisticated measurements and more careful calculations yield an overall mass-to-light ratio for Virgo which is several times higher than the one we've just computed. Virgo, of course, is not a particular large cluster, nor does it appear to be a centrally concentrated cluster which has completely virialized. Measurements from other, larger clusters yield mass-to-light ratios which are even higher, of order 200-300 solar.
The stars in typical galaxies will yield a mass-to-light ratio of order 1-10, which means that the stars in a galaxy cluster are responsible for only a few percent of the total mass.
Galaxy clusters are among the most luminous sources of X-rays in the sky: some produce more than 1045 erg/s of high-energy radiation. The appearance of clusters in X-rays and in optical light is quite different, though, as these images of Abell 1689 show (click on the image to start it blinking).

Image courtesy of
Optical: NASA/STScI. X-ray: NASA/CXC/MIT/E.-H Peng et al.
Clearly, the X-rays are coming from some non-stellar source. In fact, the space between the galaxies in a cluster is (often) filled with a very hot, very tenuous gas, mostly hydrogen (like the rest of the universe). This gas emits X-rays because it is very, very hot. Why so hot?
Well, the gas sits within a deep gravitational potential well together with tens or hundreds of galaxies. If the individual gas particles respond to the gravitational influence of the cluster in the same way that the galaxies do, then each will move with a speed which is the same as that of the galaxies, roughly v = 300 km/s. You may recall that there is a relationship between the speed of the particles in an ideal gas and their temperature:

Q: What is the temperature of (ionized) hydrogen gas
in a cluster if each proton has a typical speed
of 300 km/s?
Q: What is the energy kT of a particle
in this gas? Express in electron volts.
Now, this hot gas is generally distributed like the galaxies in a cluster: sometimes centrally concentrated around a dominant elliptical galaxy, other times divided into several big clumps. The Coma Cluster, for example, shows two lumps of X-ray emission, each one centered on a big elliptical galaxy.
The hot gas in Stephan's Quintet, on the other hand,
is spread out rather uniformly -- not suprising for
a loose group of just a few galaxies.
Here's another example, showing the X-ray emission in purple
and optical emission in red, yellow and green:
Just how much hot gas is there?
Is it more or less than the mass of the visible stars
in the galaxies?
Is it enough to account for the gravitational forces
within the cluster?
How can we tell?
The first thing we need to do is to understand the
process by which the X-rays are being produced,
and the general form of their spectrum.
The basic idea is that the gas within a cluster is
so hot that it is ionized -- completely, in the case
of hydrogen, or partially, in the case of some
heavier elements.
Space is filled with a soup of charged particles,
zooming past each other at very high speeds.
Each time one passes close to another, the
electric force accelerates it towards or away from
its neighbor, leading to ....
This process involves two particles meeting, so the amount
of brehmsstrahlung radiation will depend on the density of
electrons and the density of ions; in other words, it will
depend on the density of particles, squared.
The frequency of the emitted photon depends on the
speed of the electron;
the more kinetic energy the electron has, the higher
the energy of the photon which might be emitted.
If one goes through all the math, one ends up with
an emissivity which looks something like this:
The spectrum of this "thermal brehmsstrahlung" has some
similarities to good old thermal blackbody radiation;
note the exponential factor. However, there are also
differences: a factor of temperature to the negative one-half power,
for example.
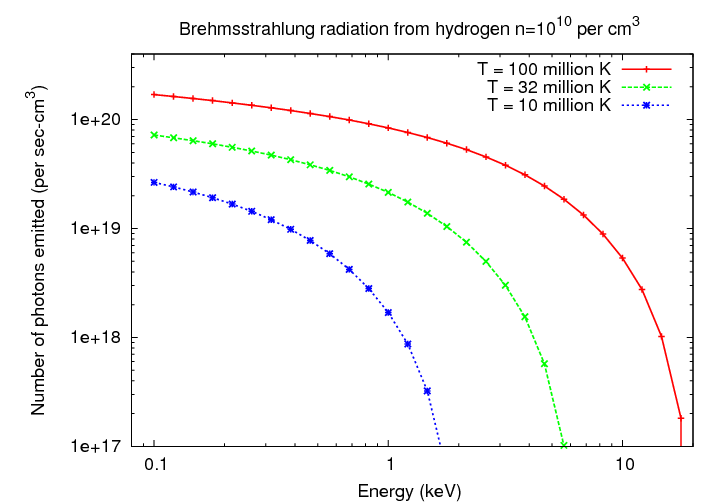
You can see a graph of the spectrum of thermal brehmsstrahlung
below.
I've chosen to plot the number of photons emitted per second
per cubic centimeter, rather than the amount of energy
emitted over some frequency or wavelength interval, because
the detectors of astronomical X-rays all count photons.
When we look at a distant cluster of galaxies, we must
peer through a screen of dust and gas in the Milky Way
(and sometimes at intermediate distances, too).
X-rays are like other electromagnetic radiation:
they can be absorbed by intervening atoms.
It turns out that low-energy, or "soft" X-rays,
are much more likely to be absorbed than high-energy,
"hard" ones.
One of the standard references for the quantitative
absorption cross-section of X-rays is a paper by
Morrison and McCammon, ApJ 270, 119 (1983).
They provide a polynomial fit to the somewhat complex
variation in absorption of X-rays in the range
of most X-ray telescopes.
If X-rays must travel through appreciable amounts of the
ISM to reach us, then the shape of the observed spectrum
will change greatly at the low-energy end.
What can you say about this spectrum of the galaxy cluster
1RXSJ153934.7-833535?
The spectrum is represented by the crosses and solid line;
I've erased a line which was a measure of the background
which had been subtracted from the signal.
Now that we understand a bit better the nature of this
X-ray emission, we might be able to figure out
just how much mass it represents.
If we make a few simplifying assumptions, we can estimate the
mass of the hot gas using quantities we can determine from the
X-ray observations.
We'll assume
where P is the pressure, ρ is the density of the gas,
k is Boltzmann's constant,
μ is the mean molecular weight of the gas,
and
mp is the mass of the proton.
where Mint is the mass interior to
the radius R
If one starts with these assumptions, and then puts the equations
for hydrostatic equilibrium together with the ideal gas law,
one can derive an expression for the mass of gas within some
radius R:
That second form of the equation uses logarithmic derivatives,
which are, basically, a description of how fast the
RELATIVE changes in one quantity are changing,
relative to the RELATIVE changes in another quantity.
For example, if I turn a thermostat
with a pointer so the pointer's position p
increases by 10%,
and as a result the temperature of the room T increases by 20%,
then the logarithmic derivative d ln T / d ln p = 2 .
In short, if two quantities are related by some sort of
power-law relationship
then the logarithmic derivative tells you what the value of
the power law's exponent is.
So, if we can make enough measurements of the X-ray gas in a cluster
of galaxies to determine the change in temperature
and density as a function of radius,
then we can in theory determine the total enclosed gravitational
mass as a function of radius.
However, things aren't quite so simple when one examines the
X-ray emission from a cluster of galaxies.
There are several complicating factors.
Let's look at one good case, in which we have detailed
X-ray observations of a cluster.
Umetsu et al., ApJ 755, 56 (2012)
combine optical and X-ray measurements of the
galaxy cluster MACS J1206.2-0847 to determine its
mass using several different techniques, including
weak and strong lensing, magnification, and X-ray
emission under several scenarios.
As you can see, the fraction of the total cluster mass
which is due to the hot X-ray-emitting gas
is pretty small.
For most clusters, we can't disentangle all these complicating
factors, and must therefore make even MORE
simplifying assumptions in order to make even
a rough guess at the enclosed mass.
One frequent method leads to what is called the
beta model.
We assume
These two assumptions lead to the conclusion that
the density of the hot gas traces the density
of all gravitational mass,
but according to some power law:
In fact, one can work out the value of this exponent β;
it depends on the ratio of the dynamical temperature --
defined by the motion of galaxies and stars through the cluster --
to the gas temperature -- defined by the motions of
gas particles.
In this equation, the symbol σ stands for the
velocity dispersion of galaxies in the cluster.
If the gravitational mass of the cluster is distributed
like an isothermal sphere, then
and therefore the gas must have a density which behaves
like
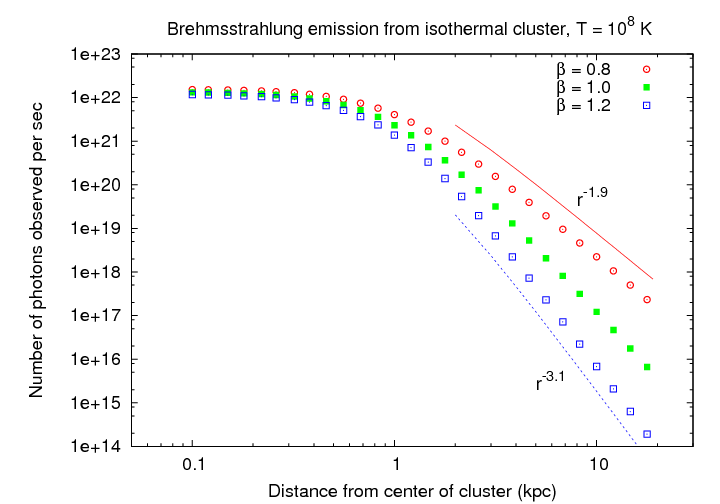
In this case, when one performs the integral along lines
of sight through the cluster to determine the observed
intensity of X-ray radiation, one finds that the total
intensity as a function of radius will be relatively
flat within the core of the cluster,
and then fall off rapidly with distance.
At large distances, the observed intensity decreases
as the radius to a power which is related to β
in a simple way:
So, we finally have a way to start with X-ray observations
and end up with an estimate of the mass of
the X-ray gas within the cluster.
The two methods don't always agree,
which is probably a reflection of the many
over-simplifications we've made along the way.
Nonetheless, the are some rough conclusions we can
make based on X-ray observations of many
clusters.
The mass of the hot intracluster gas
is
That leaves the majority (about 80%) of the mass required
to produce the gravitational motions
in the category of dark matter.

Images courtesy of
Optical: DSS; X-ray: NASA/CXC/SAO/A. Vikhlinin et al.

Images courtesy of
X-ray: NASA/CXC/INAF-Brera/G.Trinchieri et al.; Optical: Pal.Obs. DSS

Image courtesy
X-ray: NASA/CXC/ESO/P.Rosati et al.; Optical: ESO/VLT/P.Rosati et al.
A detour into the physics of X-ray emission
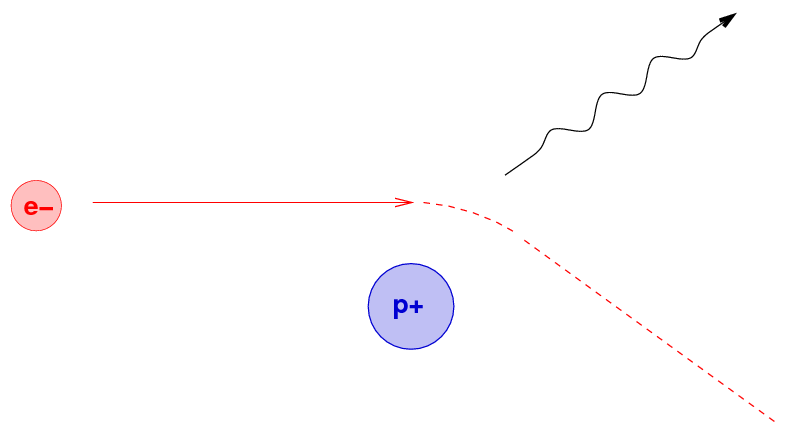
brehmsstrahlung radiation.
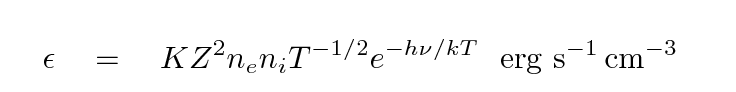
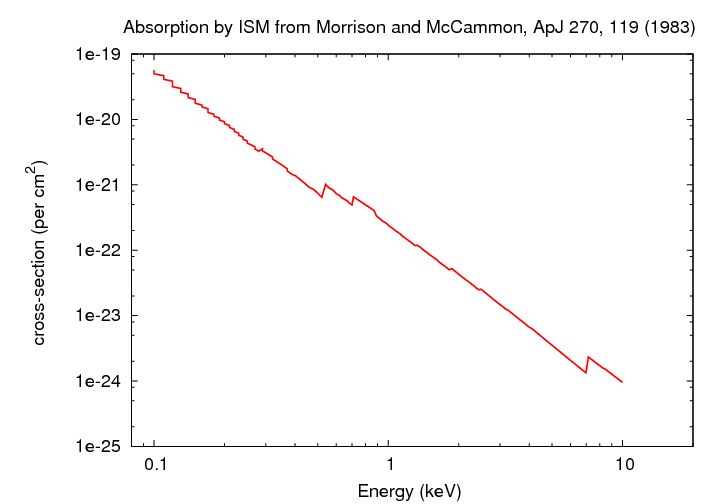
Q: What causes the little jumps in cross-section
at different energies?

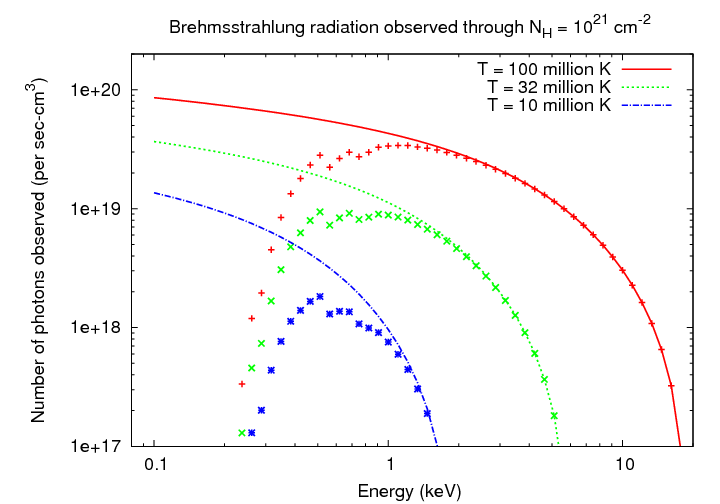
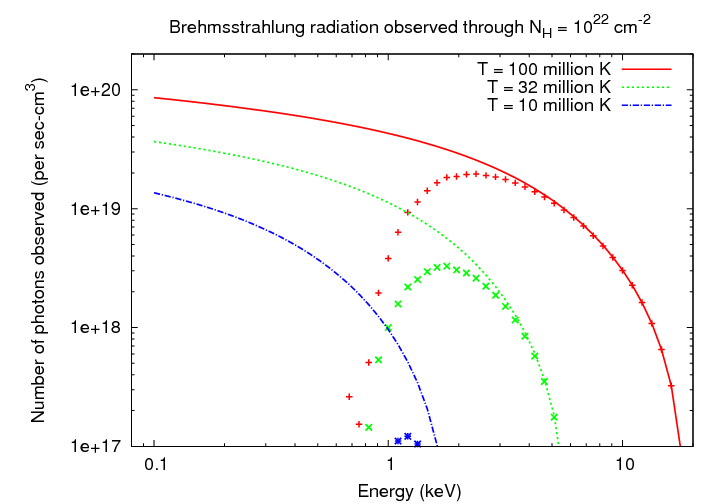
Q: What is the column density through the
disk of a big spiral galaxy like
the Milky Way?

Figure taken from
Nakanishi and Sofue, PASJ 55, 191 (2003)
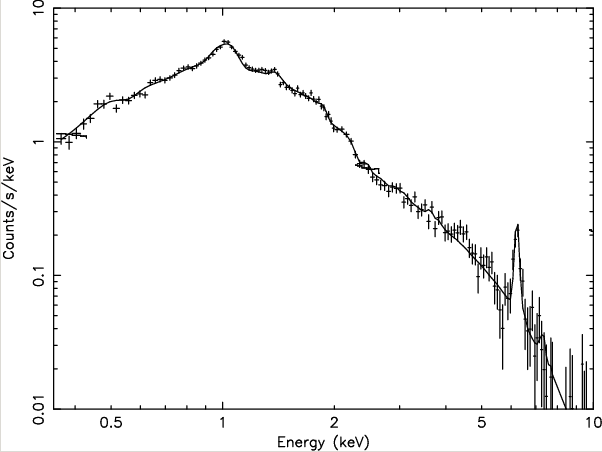
Figure taken from
Grange et al., A&A 513, 2 (2010) and slightly modified.
Back to the question: how much mass in hot gas?
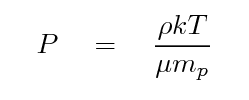
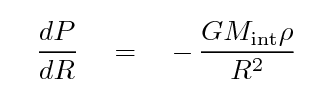
Q: Can you derive an equation for Mint
as a function of radius?
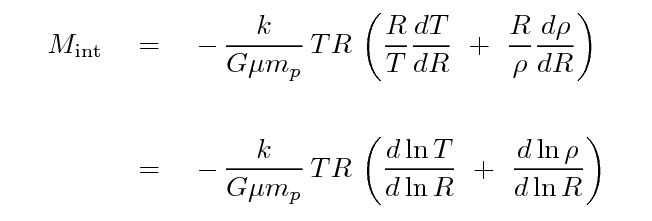
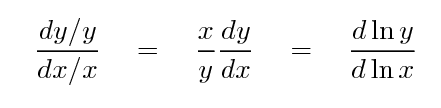
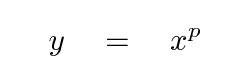
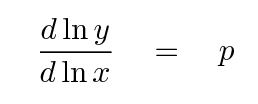
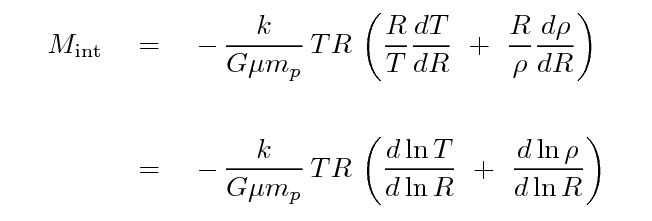

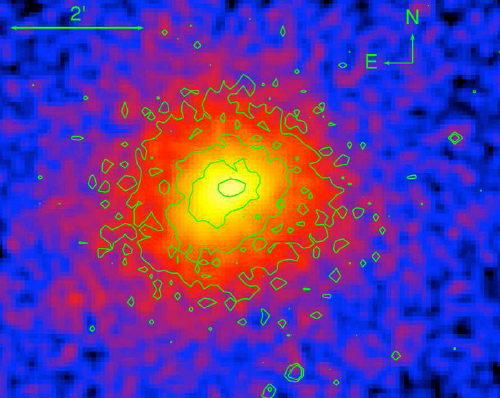
HST image from Hubblesite Gallery
Figure 10 from
Umetsu et al., ApJ 755, 56 (2012)

Figure 15 from
Umetsu et al., ApJ 755, 56 (2012)
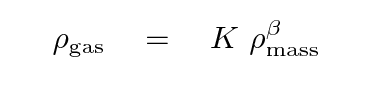
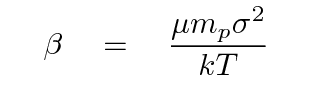



For more information
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.