Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
A photon created within an optically thick medium will be scattered or absorbed and re-emitted many times before it finally escapes. How many times? And how long will it take to escape? We can't provide an exact answer for any particular photon, but we can make a decent estimate in a statistical sense of the average number of steps required, by using random walk analysis.
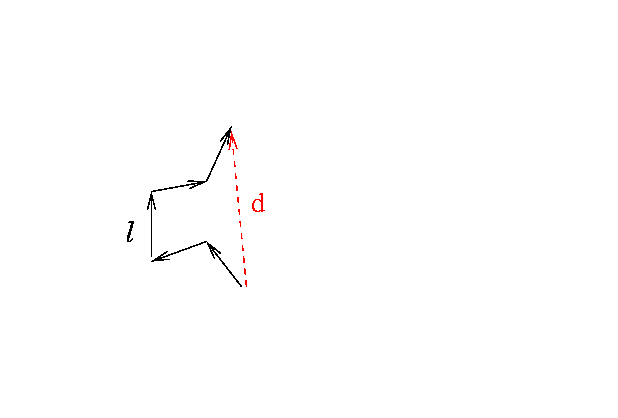
The basic idea is simple: given a mean free path ell, and a random distribution of scattering angles, determine the overall displacement d of the photon after a certain number N scattering events.
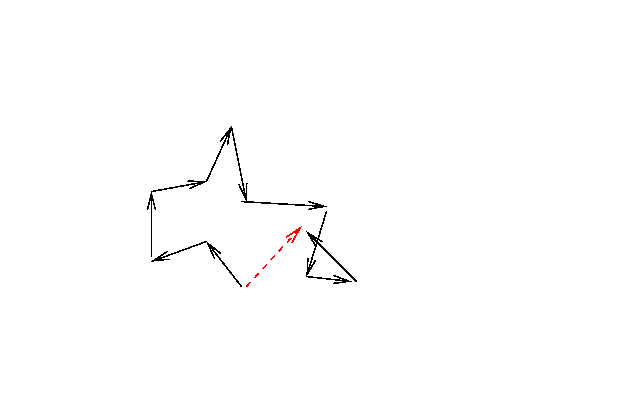
Let's follow this photon for a while. The picture above shows its progress after N=5 steps. How about N=10 ...
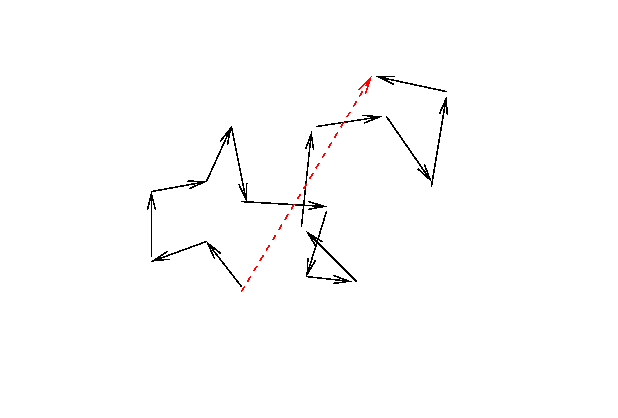
or N=15 ....
It turns out that the statistical average of the overall displacement d after N steps is simply
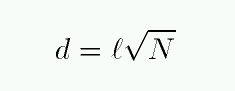
The total distance covered by the photon during this journey will of course be simply N * ell. If you know the speed of the photon -- and you do! -- then you can figure out the time it takes for the photon to make the trip.
Energy is generated at the center of the Sun by reactions in which hydrogen nuclei fuse together to form helium. Suppose that the Wicked Witch of the West waves her magic wand and turns off all fusion reactions at the center of the Sun. Would the Earth immediately enter a deep freeze?
Yes, there would be dramatic events due to gravitational forces pulling the core in on itself ... ignore them for now.
Exercise:
Your job is to calculate the time it takes for a photon created at the center of the Sun to make its way to the photosphere and escape into space. There are two limiting cases which provide over- and under-estimates of the actual time.The truth lies somewhere in between.
- Assume that the average mean free path of a photon everywhere in the Sun is the same as the mean free path in the photosphere.
- What is the mfp for a photon in the photosphere?
- How many steps would it take for a photon to move from the center of the Sun to its outer layers?
- How much time would the journey require?
- Assume that the average mean free path of a photon everywhere in the Sun is the same as the mean free path in the core the Sun.
- What is the mfp for a photon in the core?
- How many steps would it take for a photon to move from the center of the Sun to its outer layers?
- How much time would the journey require?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.