Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
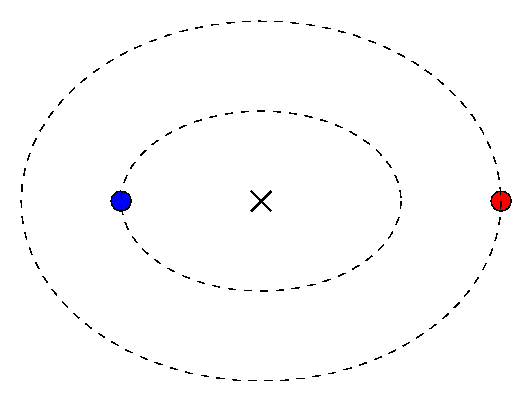
In our Solar System, the planetary orbits are relatively simple: the Sun remains (nearly) motionless at one focus of a nearly circular ellipse, and each planet moves in an elliptical orbit around it. Because the mass of the Sun is so much larger than the mass of most of the planets, we can often treat the Sun as fixed in position. The orbital motion then follows Kepler's Laws.
But what if we consider a situation in which there are two bodies of nearly equal mass? Neither one will remain fixed in place; instead, each one will move around the center of mass. The resulting orbits are still elliptical, yes, but it is not so simple to describe them.
Moreover, consider the plight of the observer, who doesn't share the ability of the theoretician to fly magically through space and watch the stellar motions from a spot far above the center of the binary system. If a real astronomer measures the position of the star in a binary system over a period of several years, she sees a very complex combination of
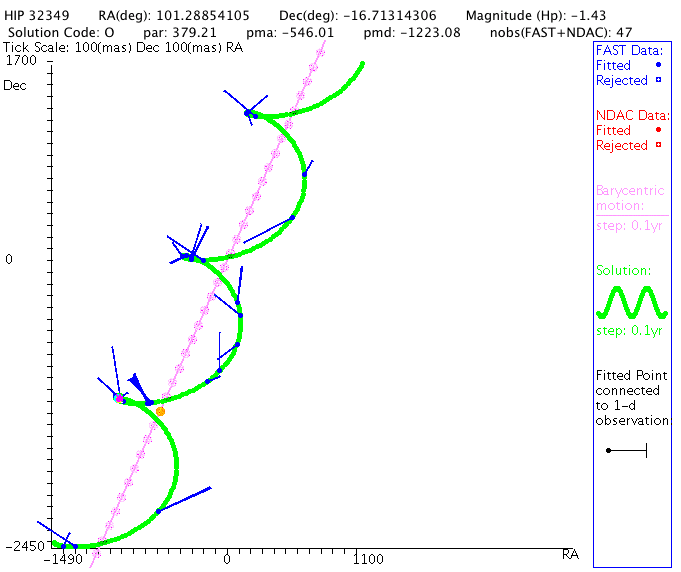
It's a real pain to deal with these extra motions. It would be much nicer if we could somehow find a way to get rid of all the proper motion and parallax, leaving nothing but the relative motion of the two stars in their orbits.
But we can! There is a simple way for astronomers to measure the orbital motion of the stars alone. It all boils down to this: measure the position of one star relative to the other.
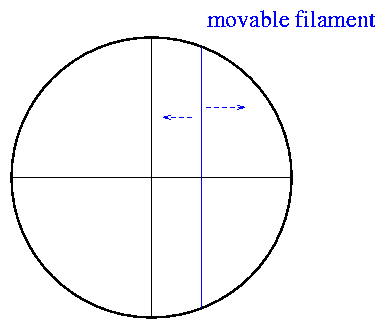
Back in the old days, astronomers used a special tool called a "filar micrometer" to make these relative measurements. It was at heart a simple device: an eyepiece with a fixed crosshair, plus a mobile filament:
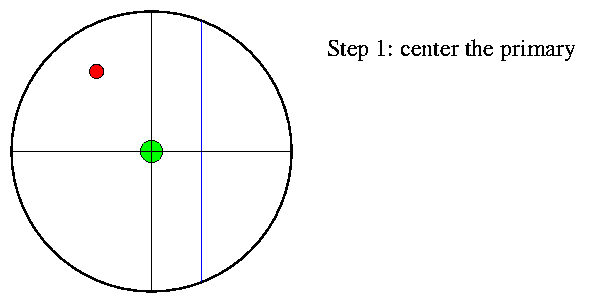
To use it, you first move the telescope so that the primary (brighter) star is centered on the fixed crosshair.
Next, you turn a screw to rotate the crosshairs so that they match the orientation of the two stars. The micrometer has a very precise mechanism which allows you to determine the angle by which you need to twist the crosshairs accurately. We call the angle -- measured Eastwards away from North -- the position angle of the binary.
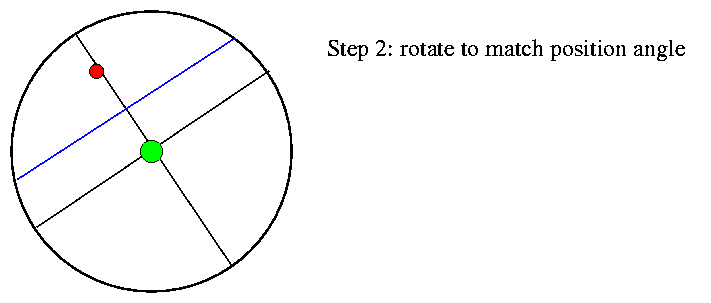
Finally, you turn a second screw to move the mobile filament until it matches the angular distance between the primary and secondary star. Again, the micrometer allows you to read this separation very precisely.
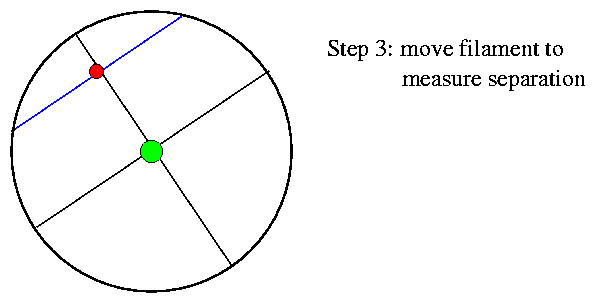
A careful observer, after calibrating his filar micrometer, could measure position angles and separations very, very accurately. Remember that anyone looking through a telescope from the Earth's surface will see any star as a fuzzy blob roughly 1 arcsecond in diameter (maybe a bit smaller on a good night). Yet consider these measurements, made by E. E. Barnard with the Yerkes 40-inch refractor.
Another astronomer had suggested that this star, DM +37 4131, might be very nearby, and thus show a large parallactic shift. Based on the table of positions above, what do you think?
The standard deviation of the measurements is
Clearly, this was a powerful tool in expert hands!
Filar micrometers were the primary instruments used for the study of double stars for many decades. Some of the great double-star catalogues are filled with measurements made by people who spent years out in the dark, peering through an eyepiece and slowly turning a screw back and forth.
Filar micrometers provide very precise values of the
But -- wait a minute. In real life, most binary stars have roughly comparable mass. That means that both stars will be orbiting around the center of mass; both stars will be moving. Yet our measurements give us only the relative motion of one star (the secondary) around the other (primary). If we try to apply Kepler's Laws to our measurements, we'll be mixing apples and oranges.
What can we do?
The answer is to transform the theoretical quantities -- the absolute mass and position of each star -- into equivalents which match more closely the observational quantities -- separation and position angle of secondary relative to primary. We can do this by defining the following:
Mass of primary m1 -> total mass M = (m1 + m2)
m1*m2
Mass of secondary m2 -> reduced mass mu = --------
(m1 + m2)
Position of primary r1 -> origin
Position of secondary r2 -> (r2 - r1)
In the reduced mass system, one of the two objects (the massive one) sits motionless at the origin while the other (reduced mass) orbits around it. The position of these two objects is exactly the same as the observed, relative position of the two real stars in the sky. That means that we can compare the observations to the model directly. Moreover, with the definitions above, we will find that the following quantities are exactly the same in the real and reduced-mass systems:
Thus, calculations we perform on the reduced-mass system will yield the same results as we would get if we could (like a theoretician) float far above the real binary star system in space.
Okay, so suppose that we do make a series of careful relative measurements of the components of a binary star.
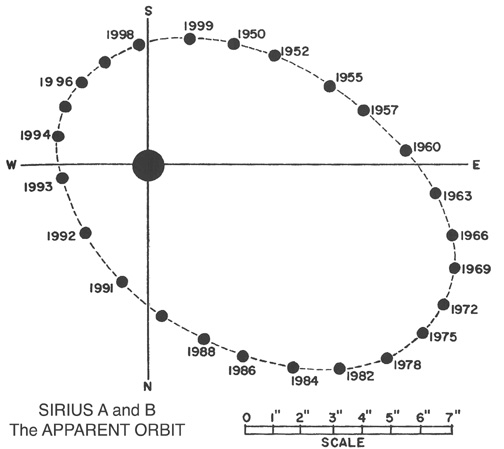
The relative positions give us the orbit in the reduced-mass system. We can easily measure a, b, e, and the period P. But what about the relative masses of the two stars? In the example above, is the primary twice as massive as the secondary? Five times as massive? Ten times as massive?
It turns out that you just can't tell ... if all you know is the relative orbit. Sigh.
After all the hard work required to draw the relative orbit, we need an extra piece of information to determine the relative masses. There are (at least) two ways to get it:
The relative displacement of the each star from the center of mass is inversely proportional to its relative mass.
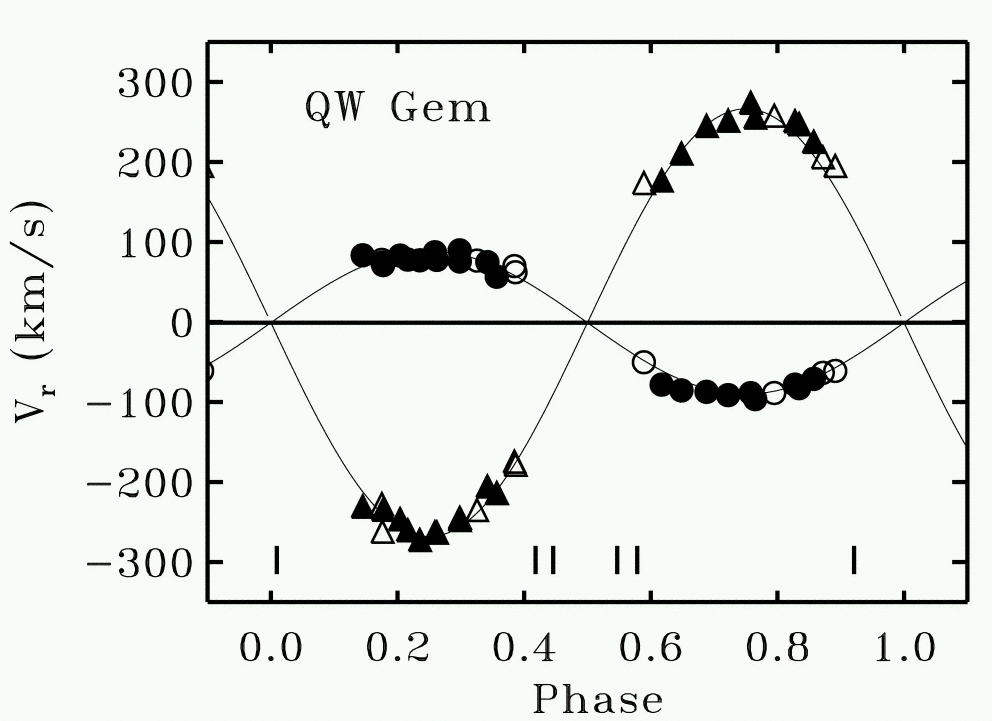
The relative radial velocity of each star away from the systemic velocity is inversely proportional to its relative mass.
Exercise: Which of the two stars in QW Gem is more massive? What is the ratio of masses in this system? What would the reduced mass of the system be?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.