Properties of the Radiation Field

We've spent some time looking at the properties of atoms and ions inside stellar atmospheres, but that's just part of the story. We now turn to the other type of denizen of these regions: photons. How do photons interact with the atoms and ions? Exactly which wavelengths are absorbed, and which escape into space?

These and other questions will occupy us for most of the remainder of this course.

So, to start, we need to spend a little time defining the properties of radiation, so that we can express ourselves properly in the discussions and calculations which will follow.

Energy, flux and intensity

Consider a beam of light moving through space:

It seems simple enough to say that "these light rays carry energy to the right", or "the beam has a certain momentum," but if we are going to use energy, or momentum, or other quantities in calculations, we need to be more precise.

We need to specify the area through which the light rays pass, and how long it takes for them all to move through it.

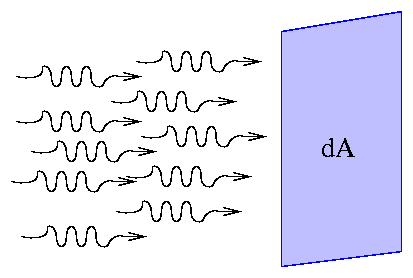
The amount of energy passing through some given area dA during some interval of time dt is called the flux of energy, often abbreviated as flux.

Exercise: What are the units of flux?

Now, if we restrict the calculations to a small range of wavelengths dλ, and write the energy contained within this range as E_λ dλ, then we can speak of the flux per unit wavelength, also known as radiative flux, or informally as "eff lambda", or "flams".

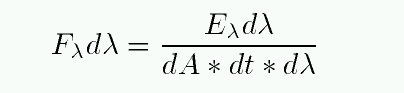
Exercise: What are the units of flux per unit wavelength?

We can be even more specific, by choosing only those light rays which pass through the area and leave through some solid angle dΩ

If this solid angle happens be to perpendicular to the surface (so the light rays pass straight through), as shown in the figure above, then things are straightforward. But if we choose to look at radiation which comes through the area at some oblique angle θ, like this:

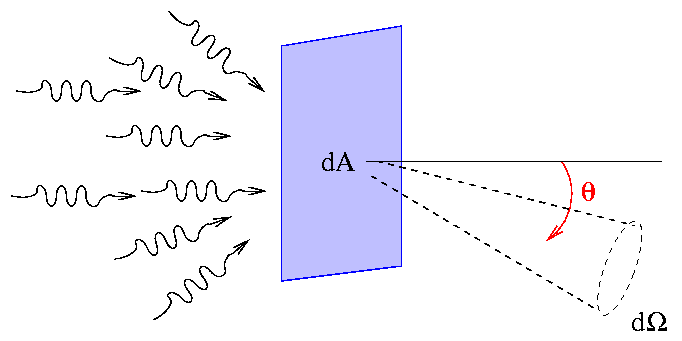
then the effective area of our little patch dA becomes somewhat smaller: dA cos(θ). So, if we consider only those light rays within our little range of wavelength which pass through the little patch in this particular direction, we end up with the specific intensity, sometimes called plain old intensity.

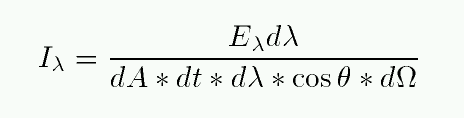
Exercise: What are the units of specific intensity?

Now, in general, the intensity can vary with direction: a searchlight, for example, produces a very high specific intensity straight ahead, and much smaller specific intensities to the sides. For most of our purposes, the intensity will be the same in directions, making it isotropic. If you are trapped inside a meat locker, you feel the same (lack) of radiation in all directions.

Surface brightness

Astronomers like to take pictures of stars and galaxies. In the context of flux and intensity, there's an important difference between these two classes of objects:

stars are (usually) unresolved
galaxies are (usually) resolved

We normally measure the flux from an object on a two-dimensional detector by adding up all the light which falls within some circular area on the detector. That corresponds to some very small solid angle dΩ from the point of view of the shining object. Suppose we decide to add up all the light within a region the size of the small red circle:

All the light from the star will fall completely within this area, but only a small fraction of the light of the galaxy will fall within this area.

Now, if we imagine moving the star and galaxy farther away, so that each is at twice its original distance, what will happen to our measurements?

The apparent size of the star hasn't changed at all -- it's still unresolved. Therefore, all the light from the star still falls within our aperture. However, since the star is now twice as far away, we must be receiving only one-quarter as much energy from it. Hence, the total detected energy, or number of counts, must go down by a factor of four.
The apparent size of the galaxy HAS changed: it is now half the original angular diameter. That means that our measurement region now covers a larger portion of the total galaxy. However, as long as the galaxy is still larger than the measurement area, we will find that
- although the intensity of light from each little piece of the galaxy must have decreased by a factor of 4, since it is now twice as distant ...
- our measurement area now includes many more little pieces of the galaxy; in fact, it includes 4 times the number of little pieces
As a result, the amount of light we record inside the measurement area will not decrease very quickly. If the galaxy is uniformly bright across its entire extent, then the detected light will remain exactly the same.

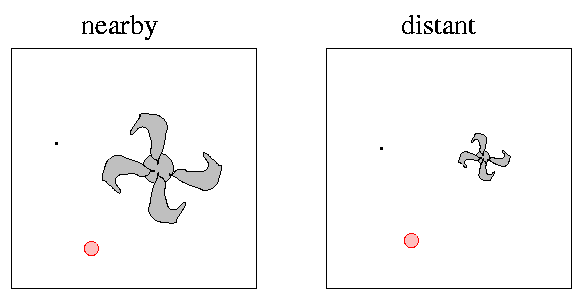
Astronomers call the amount of light gathered within a specific measurement area surface brightness. We typically choose arcane units, "magnitudes per square arcsecond", which are easy to measure in practice, but hard to connect to theoretical quantities like specific intensity.

Exercise: The disks of spiral galaxies tend to have very similar surface brightness values -- roughly magnitude B = 21.6 per square arcsecond. Explain exactly how some astronomer must have determined this value. In other words, explain the steps he must have taken with his telescope and camera, and with his computer or calculator.

Energy density

Photons carry energy, of course, so if some region of space is filled with photons, it must also have some energy. Let's define the specific energy density of some region to be the energy within some volume of space due to photons with some small range of wavelengths between λ and λ + dλ. As your textbook shows, we find

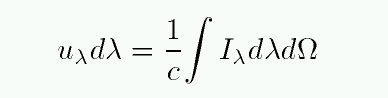
or, for an isotropic radiation field,

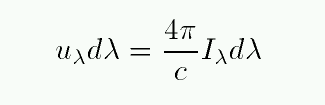
For the very common case that the radiation is emitted by a blackbody, the specific intensity is given by the blackbody spectral function B_λ, which you can find way back in chapter 3 of your textbook.

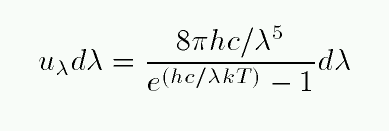
If you integrate over all wavelengths, you end up with a simple expression for the energy density:

Exercise:

What is the energy due to photons contained within a box of volume V and temperature T?
How does the energy stored in the form of radiation change if we double the temperature?
What is the energy density due to kinetic energy of gas particles within a box of volume V and temperature T?
How does the energy stored in kinetic energy of matter change if we double the temperature?
Suppose we turned off the lights in this classroom and closed the curtains, so that no external light could enter the room. Estimate the energy stored in photons within the room.

Momentum and pressure

In addition to energy, photons carry momentum:

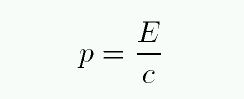
When a photon strikes a little surface and bounce off,

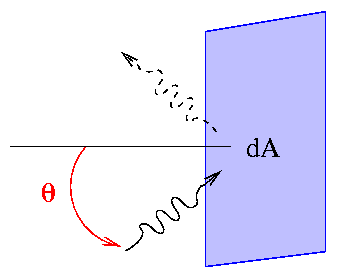
they transfer their momentum to the little surface. This change in momentum acts as a force, pushing the little surface backwards. The pressure exerted by all the photons incident on a little surface is just the total force (change in momentum per unit time) divided by the area dA of the surface. As your text shows, we can express the radiation pressure as

If the radiation field is isotropic, then this pressure becomes

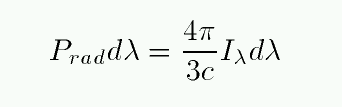
If one integrates the pressure due to photons of all wavelengths produced by a blackbody, we find a particularly simple result:

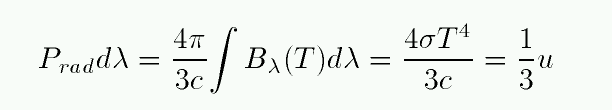
Exercise:

Joe creates a solar sail and releases it halfway between the Earth and Moon. Can he use the equations above to calculate the pressure and hence force on his sail, or does he have to modify them in some way?

At the center of the Sun, the temperature is roughly 10 million K. What is the radiation pressure in that place? Compare it to the atmospheric pressure on Earth at sea level, and the water pressure at the bottom of the Marianas Trench (which is about 10 km deep).

For more information

Ken Freeman's paper on the disks of spiral galaxies, published in 1970, was the first to mention their nearly uniform surface brightness.