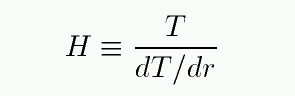Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Thermodynamic Equilibrium, Local and otherwise
We are interested in the details of light's passage through
the outer layers of a star.
One of the crucial factors in this process
is the "temperature" of the gas.
But -- what exactly do we mean by "temperature"?
Is it possible to define a temperature in
these exotic regions?
It will turn out that one can define
a "temperature" in some very strict sense
only under special conditions,
called thermodynamic equilibrium,
which do not actually apply in the atmospheres
of real stars.
However, for many purposes,
one can define a sort of local thermodynamic equilibrium
which is good enough to bring theory
and observation into agreement.
The many different temperatures
Let's count the ways we could try to describe the temperature
of the photosphere of a star.
- Effective Temperature
- Measure the radius and luminosity of a star. Find the
temperature of a blackbody which would produce the
same total amount of energy:
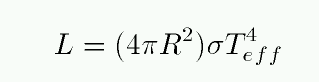
- Color Temperature
- Measure the spectrum of a star, or, more commonly,
its color via the difference of magnitudes in two filters.

Find the
temperature of a blackbody which would produce a spectrum
of the same shape, or the same difference in magnitudes
when observed through those filters.

- Excitation temperature
- Measure the ratio of atoms in two energy levels of some
neutral atom; say, the n=2 to n=1 ratio of hydrogen.
Using the Boltzmann equation,
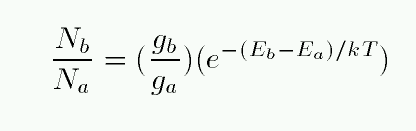
determine the temperature which would reproduce the
observed ratio.
- Ionization temperature
- Measure the ratio of atoms in two ionization stages;
say, ionized hydrogen to neutral hydrogen.
Using the Saha equation,
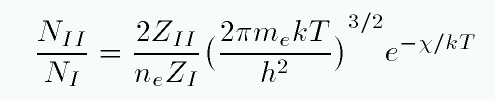
determine the temperature which would reproduce the
observed ratio.
- Kinetic temperature
- Measure the speed of particles in the gas.
If they follow a Maxwell-Boltzmann distribution,
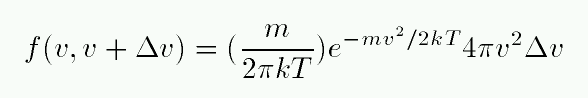
determine the temperature which would reproduce the
observed distribution.
This is often simplified to "measure some average speed
of particles, and compare to the average speed of
a Maxwell-Boltzmann distribution."
Exercise:
- Which of these is simplest to measure, in practice? What
observations would you need?
- Which of these is hardest to measure, in practice? What
observations would you need?
In some very simple situations,
all these temperatures might be exactly the same.
For example, if we build a box, fill it with some gas,
heat the walls of the box to a uniform and steady temperature,
and wait a bit, we will find that a single
temperature T will fit into all of these equations.
In such an ideal case, we say that the gas has achieved
thermodynamic equilibrium.
Two of the hallmarks of thermodynamic equilibrium
are isotropy -- properties are the same in all directions --
and homogeneity -- properties are the same in all places.
If we consider an entire star as a whole, neither condition
is true: the center of a star is much hotter than its outer
regions, for example.
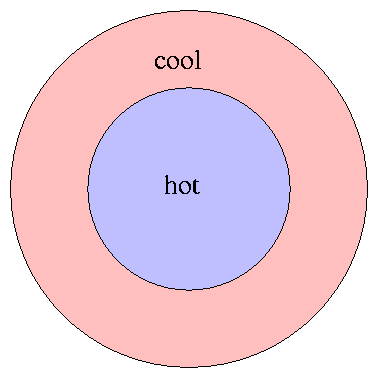
Rats! If we are trying to understand
the detailed interaction of light and matter
inside a star, it would be very, very convenient if we could
use a single value, T, to predict the
speed of gas molecules, the excitation of atoms,
the spectrum of radiation, etc.
But it appears that real life is more complicated ....
... unless, perhaps, we can find some way
to limit ourselves to a small enough piece of the star
that matter and radiation are at least
approximately in thermodynamic equilibrium.
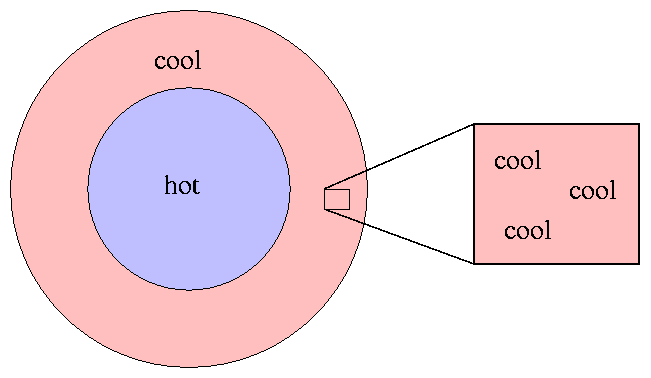
But how small does the piece have to be?
Mean free path (mfp)
It will soon become important to know how far
an atom, molecule, electron, photon -- let's just
say some "particle" -- will
travel through the tenuous gas of the
atmosphere before running into something.
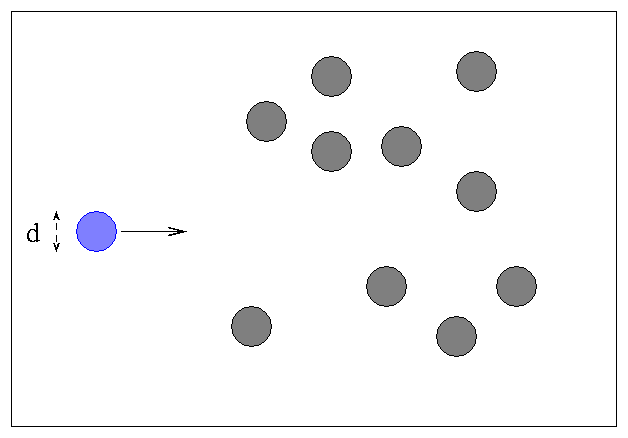
If we have a gas of atoms with typical diameter
d and radius r = d/2,
with density n atoms per unit volume,
the question is -- how far will the blue
particle typically travel before it strikes
an atom?
We can simplify the calculations by imagining
an equivalent situation,
in which the blue particle becomes twice as
big and all the other particles shrink
down to perfect little points:
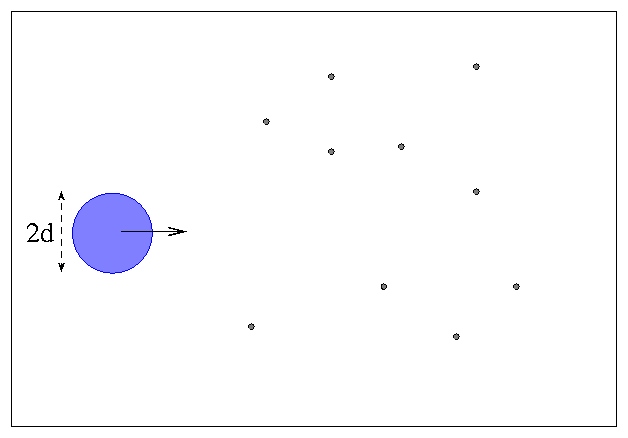
Collisions between the blue particle and others
will occur just as frequently now as in real
life, but we don't have to worry about
the mathematics of intersecting circles anymore.
Now, as the blue particle moves through the sea
of other particles, it will sweep out a
cylindrical path ...
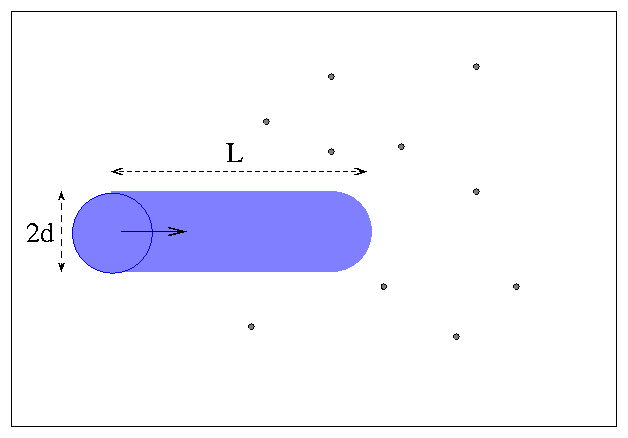
The mean free path is the average distance
the blue particle must move until another particle
falls within the volume it sweeps out.
That's just another way of describing the distance
between collisions.
Exercise:
- Express the volume of the swept-out volume
as a function of the distance L.
- At what distance will an average of one
particle fall within the volume?
- Here in this classroom,
the density of oxygen molecules is about
1.0 x 10^(-3) g/cc.
Estimate the mean free path of an oxygen molecule.
- In the solar photosphere,
the density of hydrogen atoms is about
2.5 x 10^(-7) g/cc.
Estimate the mean free path of a hydrogen atom.
Local Thermodynamic Equilibrium
Consider the motion of an individual atom in the
stellar photosphere.
We know that the temperature must gradually
decrease from the center outwards towards
the edge.
If the mean free path (mfp) of the atom
typically takes it from a region of one temperature
to a region with a different temperature,
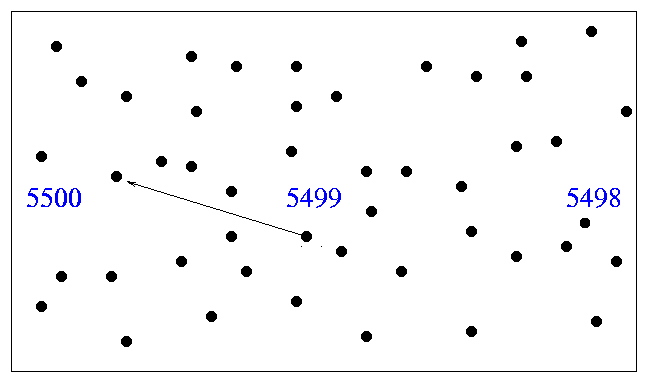
then it will constantly be changing its properties
with every collision.
That means that we will never be able to describe it
for any length of time as having some well defined
temperature.
On the other hand, if the mean free path of the
atom is very small compared to the distance over
which the temperature changes,
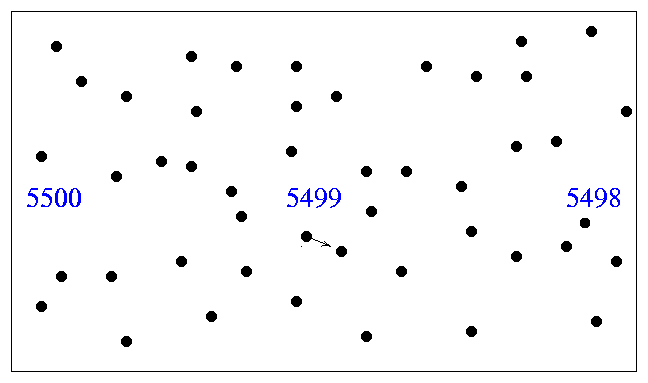
then the atom will collide many times with other
atoms, all of the same temperature,
before it can possibly reach some region
with a different temperature.
In this case, the speed of atoms within some small
region may very well be described
by a Maxwell-Boltzmann distribution
with a definite temperature.
So, over what distance does the temperature change in the sun's photosphere?
It sounds like a simple question, but what
does it mean?
- over what distance does the temperature change by 100 degrees?
- over what distance does the temperature change by 1000 degrees?
- over what distance does the temperature change by a factor of 2?
- over what distance does the temperature change by a factor of e?
Physicists often choose to define the distance over which some property
changes "significantly"
as the ratio of the LOCAL value to the LOCAL GRADIENT:
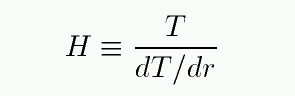
The distance defined in this way is called the (temperature)
scale height.
Use the graph below to estimate the temperature scale height of the
solar photosphere:

Exercise:
- What is the temperature in the middle of the photosphere?
- How much does the temperature change from top to bottom of photosphere?
- What is the distance from top to bottom of photosphere?
- Calculate the scale height H of the solar photosphere.
Compare the scale height H of the solar photosphere
to the mean free path of its hydrogen atoms.
May we consider the atoms in the photosphere to be in LTE?
For more information
-
NASA SP-402 contains lots of information about the
Sun, based on the Skylab experiments.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
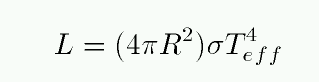


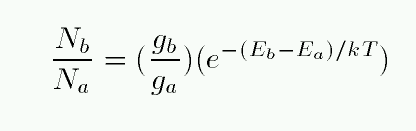
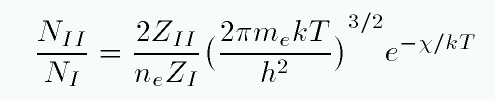
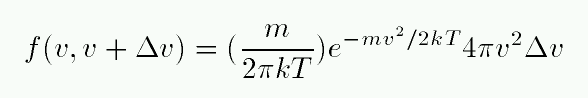
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.