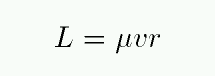
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The two-body problem is simple: one can start with Newtonian mechanics and end up with a complete description of the system's motion. But what about the three-body problem -- three bodies acting under their mutual gravitational forces? That can only be solved analytically in a restricted range of cases. And the more general N-body problem is completely impossible to solve analytically. Rats.
However, although we can't specify the detailed motion of every single object in an N-body system, it turns out that we CAN come up with a few -- a very few -- properties of the entire ensemble which
We call these integrals of motion. They can be very handy for some purposes, allowing us to predict the "bulk" behavior of a large group of stars, for example, even if we can't follow any single star in detail.
Let's restrict ourselves to the simplest non-trivial case, the two-body problem, and look at the integrals of motion. It turns out that one can find expressions for them in terms of the standard orbital parameters (semi-major axis a, eccentricity e, etc.).
A two-body orbit lies in a plane. In the reduced-mass case, one object moves while the other sits motionless. The angular momentum is easy to calculate at perihelion and aphelion, when the orbital motion is exactly perpendicular to the line joining the two bodies. It has magnitude
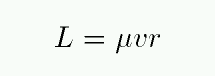
and so at aphelion, in particular,
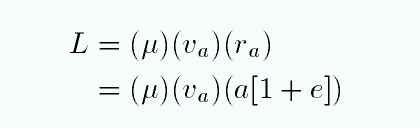
Now, you may recall from the homework assignment last week that one can express the speed at aphelion in terms of the quantities
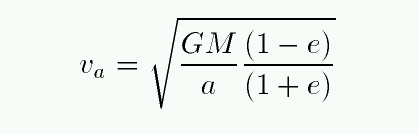
And inserting this into the equation for angular momentum at aphelion yields

Exercises:
The other integral of motion (yes, there are only two) in a binary orbit is the total energy of the system. You may recall the term mechanical energy from introductory physics; it describes the sum of kinetic and potential energies. In the case of a binary star, the only significant potential energy is due to gravity.
We can write the total energy of the reduced-mass orbit as

Now, since we know this energy is conserved all the way around the orbit, let's again pick a convenient time in order to re-write the expression in terms of the orbital shape parameters. At aphelion, remember, the velocity is
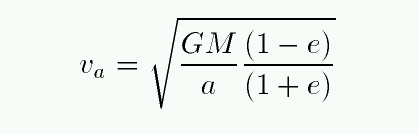
so we can write the energy as
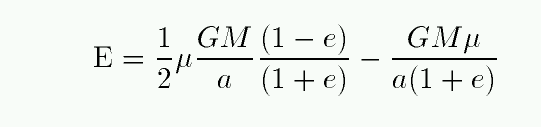
With a little algebra, this simplifies to a very familiar-looking expression:
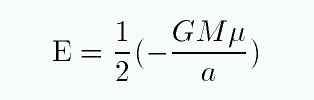
The time-averaged orbital separation turns out to be exactly the semi-major axis a, so that
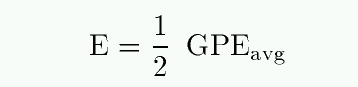
Exercises:
It turns out that any gravitationally bound system, such as the Earth and Moon, or Sun and planets, or the Milky Way Galaxy, has a negative total energy. This provides one easy way to test if one particular object is bound to another -- say, to see if a space probe will orbit around Mars, or fly past it and never return. Simply calculate the sum of kinetic energy of the probe relative to Mars, and the gravitational potential energy of the probe relative to Mars. If the sum is positive, then the mission must be a flyby (unless, of course, the probe fires its engines to slow itself down as it goes past....)
So, we now know several things: the total energy of a two-body orbit is constant, it is composed to two pieces -- kinetic energy plus gravitational potential energy -- AND that constant is equal to half the time-averaged gravitational potential energy. But, wait a minute -- let's write that down.
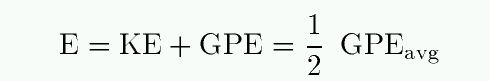
If we consider the time-averaged value of the items in the middle of this equation -- just as we are using the time-averaged value of the GPE on the right-hand side -- then we can write
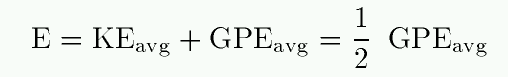
Or, putting KE on one side and GPE on the other side,
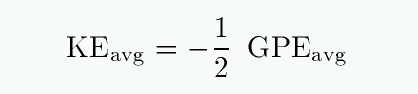
Does this equation hold all the time? That is, at any moment in its orbit, does the kinetic energy of a body equal negative one-half times its potential energy? For a circular orbit, yes. But for an elliptical orbit, no. Look at the KE and GPE for an Earth-like planet in an elliptical orbit around the Sun:
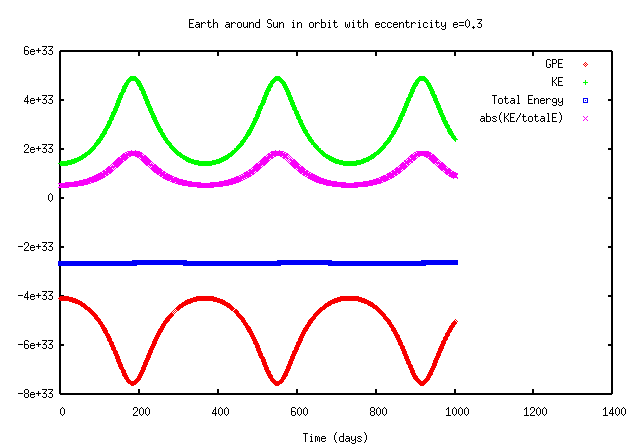
Note that the ratio of KE to total energy (shown above in light purple) does change over the course of the orbit: the fraction of the total which is kinetic energy rises when the planet is near perihelion, and falls below the average near aphelion. The nice, simple relationship -- KE equals negative one-half GPE -- only holds when averaged over a complete orbit.
The connection between the total energy of a gravitationally-bound system and its GPE and/or KE is part of the virial theorem. It turns out that the virial theorem applies not only to binary stars, but to many closed systems in equilibrium. For example, we can apply it to
Determining the mass of an object is very difficult, as you know; there just aren't many ways to sense it remotely. But determining the kinetic energy of an object is pretty easy: we can use its apparent motion plus its distance to calculate speed; or we can look at it through a spectrograph and use the Doppler shift to find its radial velocity. Once we have some guess for its kinetic energy, the virial theorem allows us to estimate its gravitational potential energy ... and THAT gives us a hint about its mass. The sequence
measure properties -> KE -> use virial theorem -> GPE -> massappears over and over again in astrophysics.
For a circular orbit, the virial theorem's relationship between KE and GPE holds for all times:
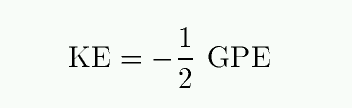
So
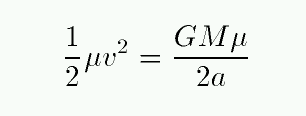
That means that the velocity of a planet in a circular orbit goes like its distance from the Sun to the negative one-half power: planets close to the Sun should orbit quickly, and planets far from the Sun should orbit slowly.
Exercise:
Is there some way to bring the orbital period into this equation? Well, the period is just the total distance around the circumference of the orbit divided by the speed of the body, so we can substitute and get

Aha! Now all we have to do is re-arrange the terms to put P on the left and a on the right, and we end up with
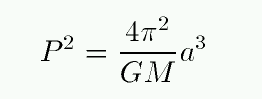
Kepler's Third Law strikes again.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.