 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The virial theorem postulates a simple relationship between the average kinetic energy and average gravitational potential energy of bodies in a gravitationally bound system:
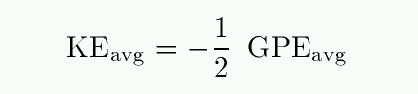
The right-hand side depends on some way on the mass of the entire system -- which is very difficult to observe in any direct way. The left-hand side, on the other hand, can be estimated if we can measure the motions of bodies in the system. Thanks to the Doppler shift, we can determine the motion in the radial direction very easily. Astronomers therefore rely heavily on the virial theorem to turn an easily observed quantity, velocity, into an obscure one: mass.
Remember that there are several assumptions that one must make while carrying out all the steps involved in the calculations:
Applying the virial theorem to clusters of stars or galaxies will certainly not yield EXACT masses ... but it's sometimes the only game in town.
You all know what a galaxy is, right? A collection of billions of stars, orbiting their collective center of mass. Some have pretty spiral arms with obvious clouds of dust

some are smooth, round balls of stars

and some look like train wrecks.

Some galaxies are hermits: isolated in space, far from any neighbor. Others -- like our own Milky Way -- belong to a village: a small group with tens of members. But many galaxies live in the big cities: cluster of hundreds to thousands of galaxies, like this:

What properties of galaxy clusters can we measure? Some of the obvious ones are:
Let's concentrate on the last item in the list: by calculating the range of radial velocities of galaxies in a cluster, we can estimate its mass. We follow the same steps as yesterday, when we measured the mass of a globular cluster:
If you look up at the sky in the early evening during in the late spring or early summer, you'll see the constellation of Coma Berenices (Berenice's Hair), not far from the bright star Arcturus:
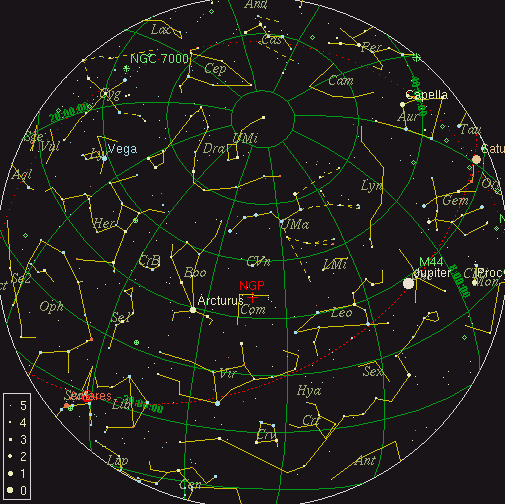
If we zoom in on Coma, we see, well, a rather unimpressive set of faint stars.
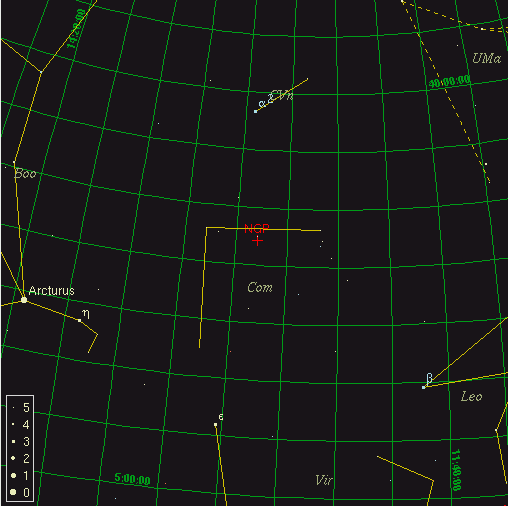
But, if we look past the stars in our own galaxy, out far into the deep reaches of space, we discover that there are a LOT of galaxies in this direction:

There's another clump just south of Coma, in the constellation Virgo.
A deep image of this region of the sky shows these galaxies clearly, whether taken in the optical or the X-ray part of the spectrum.
Fritz Zwicky was the first to notice a peculiar property of the radial velocities of galaxies in the Coma cluster.
Exercise:
- start with this table of radial velocities for galaxies near the core the Coma Cluster ,
taken from "A catalogue of velocities in the central regions of the Coma cluster", by Biviano et al., Astron. Astrophys. Suppl. Ser. 111, 265 (1995).- use the column labelled "RV", which gives the measured radial velocity in km/sec
- watch out for outliers: galaxies which appear in the same direction as the Coma Cluster, but which are actually much closer to us, or much farther away. You can recognize them by their very different values of radial velocity
- what is the systemic radial velocity of the Coma Cluster?
- what is the radial velocity dispersion of the Coma Cluster?
- assuming that the velocity distribution is isotropic, what is the average value of (3-D space velocity squared) for galaxies in the cluster?
Compare your value for the square of the radial velocity to that of Zwicky (who uses the symbol v-sub-s to mean "radial velocity")
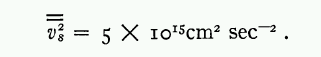
Okay, this gives us the information we need on the left-hand side of the virial theorem:
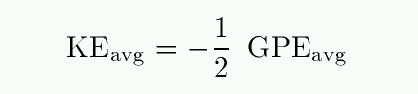
But for the right-hand side, we need something like the typical radial distance from the center of the cluster. Look again in the this table of radial velocities. The third and fourth column give the angular distance of each galaxy from the center of the cluster, west and north, respectively, in units of arcseconds. The distance to the Coma Cluster is roughly 100 Mpc.
Exercise:
- what is the typical distance of these galaxies from the center of the cluster, in parsecs? In AU?
- use the virial theorem to estimate the mass of the Coma Cluster. Express your result in solar masses.
Zwicky's estimate of the distance to the cluster was significantly smaller than our current value, so his calculation of the mass of the cluster was also significantly smaller. But he noticed a troubling discrepancy in the ratio between the mass of this cluster and the amount of light emitted by its galaxies, and, since that ratio is independent of distance, the puzzle remains to this day.
Zwicky had an estimate of the mass of the entire Coma Cluster. He counted roughly 1000 galaxies in the cluster, so he could compute an average mass per galaxy.
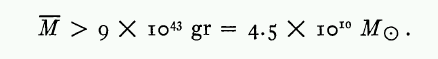
He also knew roughly how much light a typical galaxy emitted:
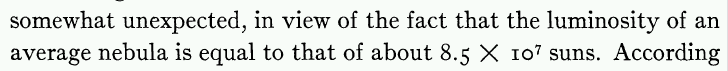
Therefore, Zwicky reasoned, the ratio of mass to light for galaxies in this cluster must be
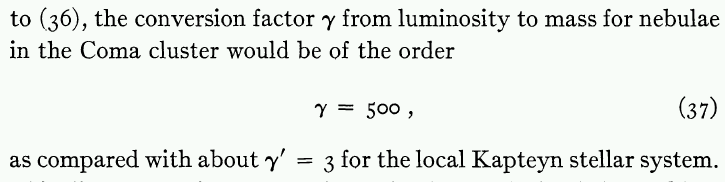
which, as Zwicky noted, was much, much, much larger than the ratio of mass to light for stars in the local solar neighborhood.
What might we conclude?
Zwicky's 1937 paper does not pick out any one of these possible explanations in particular, though it describes in detail items 2 and 3. In recent years, explanation number 4 -- the existence of some "dark matter" in clusters of galaxies -- has become the most popular. The discrepancy between mass-derived-from-gravity and mass-derived-from-light appears again and again in many large systems: individual galaxies, like the Milky Way, clusters of galaxies, even clusters of clusters of galaxies.
Observations of large portions of the universe suggest that the "dark matter" outmasses the "normal matter" by a factor of ten to one hundred. In other words, the ordinary matter we see here on Earth -- atoms and molecules and trees and people -- accounts for perhaps one percent of all the matter in the universe!
But what is this "dark matter?" It appears to interact with ordinary matter only by the gravitational force, and not by the stronger electromagnetic force (or the strong or weak nuclear forces). That means that if I tried to hold a chunk of it in my hand, it would fall through my hand and down towards the center of the Earth! Scientists have spent several decades trying to build experiments which might detect this non-baryonic material. Alas, no luck so far.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.