The Expanding Photosphere Method (EPM) of measuring distances

The Saha equation suggests that the range of temperature over which hydrogen switches from neutral to ionized is relatively narrow. Under special circumstances, we can use this fact to make rough estimates of the distances to exploding stars -- estimates which bypass many of the intermediate steps in http://spiff.rit.edu/classes/phys240/lectures/parallax/parallax.html"> the cosmological distance ladder. Because it provides a direct measure of the distance to galaxies far, far away, astronomers use the Expanding Photosphere Method as a check on other methods, even though it does involve some simplifications and approximations. Let's see how it works.

Simple physics in a Type II Supernova

When a very massive star (more than 8 or 10 solar masses) reaches the end of its life, it contains a very large, extended outer envelope of hydrogen, surrounding a dense, compact, core of heavier elements.

When the star runs out of fuel at its core, the core collapses on itself, then rebounds, sending a shock wave outwards. The shock wave

heats the outer envelope of the star to over 100,000 Kelvin (ionizing its hydrogen completely)
pushes out outwards at 5,000 to 10,000 km/sec

The outer envelope shoots outwards, moving so fast that it easily escapes the gravitational pull of the central material. As a result, the ejecta move at a nearly constant speed, making the star appear to grow larger in a linear way: twice as big after two days, three times as big after three days, etc.

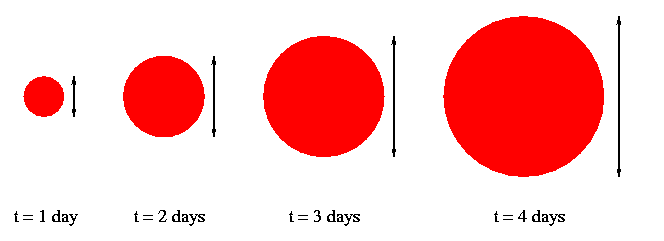
Now, as time goes by, the energy stored within the hot gas of the star's outermost layer radiates away into space:

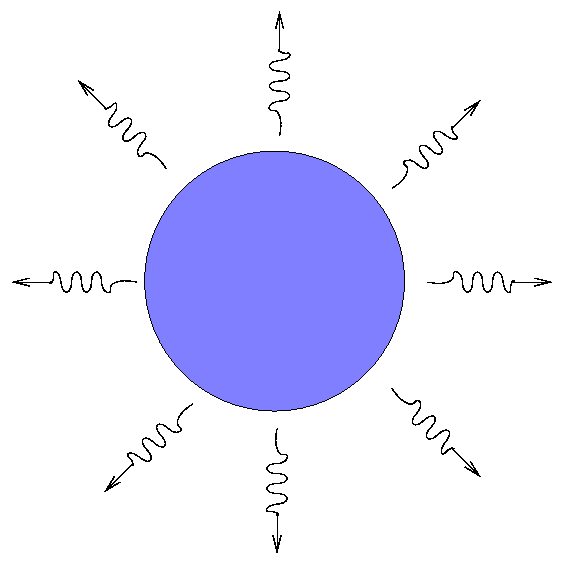
And, as a result, that outermost layer cools off:

Something special happens when the outermost layer of the star reaches the temperature at which hydrogen starts to recombine and return to the neutral atomic state. In ordinary stars, the transition takes place between 9,000 and 11,000 Kelvin. In the outer layers of a supernova, the densities are considerably lower than those in the photosphere of a Sun-like star. Look at the Saha equation again:

Exercise: If the density decreases, what happens to the temperature at which hydrogen switches from neutral to ionized?

In a typical Type II supernova, the critical temperature is around 4,000 to 6,000 degrees.

The opacity of neutral vs. ionized hydrogen

We will discuss opacity later on in this course, but a very brief summary will suffice for the current purpose.

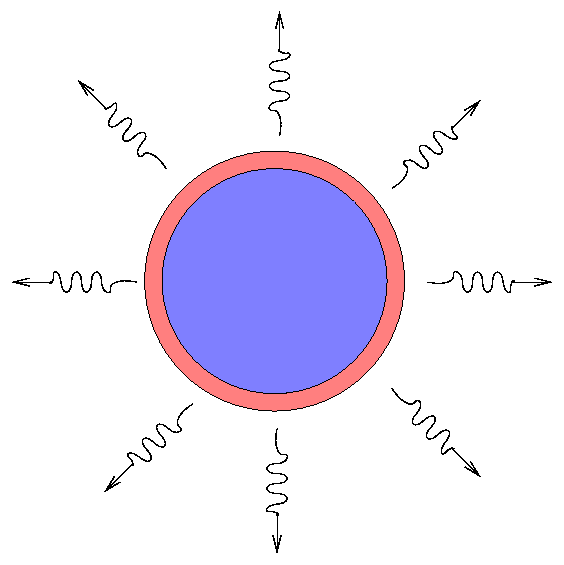
ionized hydrogen has a very HIGH opacity
neutral hydrogen has a very LOW opacity (except at a few special wavelengths)

While the entire atmosphere is hot enough to be ionized, it is all opaque. Photons from the inner layers are unable to escape into space; only the photons from the very outermost layers can fly away and be observed:

But as soon as a layer of gas cools down to the critical temperature and becomes neutral, it also becomes transparent to radiation from the hotter layers beneath it.

So, as time goes on, the outermost layers become transparent, and we see deeper and deeper into the interior of the expanding star. However, by a convenient coincidence:

the interior of the star is originally very dense ...
but the entire star is expanding outwards with time

the density and hence the temperature of the gas at the opaque/transparent boundary -- which we could call the effective photosphere -- remains roughly constant. In a typical Type II supernova, there's a period of several weeks to months during which we see an Expanding Photosphere of roughly constant temperature, of about T = 5000 K.

The basic EPM method

The result of all this is that for a period of several weeks, a Type II Supernova will remain in the so-called plateau phase

it appears to grow linearly with time, at a speed we can measure via the Doppler shift of lines in its spectrum
it maintains a roughly constant temperature -- about 5,000 Kelvin -- during the expansion

This means we can calculate the absolute size of the star, in meters, at any time:


 radius of star R = (expansion speed) * (time since explosion)

Now, if we know both the size and temperature of an object, we can calculate its luminosity from basic physical principles:

So, by measuring the Doppler shift of lines in an expanding Type II supernova, and knowing something about its atmosphere, we can calculate its intrinsic luminosity. Comparing this to its apparent brightness, we can figure out its distance via the inverse square law.

Give it a try!

Let's see how well this method works by trying it in one particular case. In a paper published in 1992, Schmidt, Kirshner, and Eastman applied the EPM technique to 10 different Type II supernovae. Here's their compilation of data on SN 1970G (which are based on observations published years ago).

Their model of the photosphere is considerably more sophisticated than ours, so the temperatures they derive at early times are somewhat higher than the values I've mentioned above. Let's pick the observations made at late times, when the temperatures are roughly 6000 K.

Exercise:

pick one row near the end of the table
calculate the number of seconds since the explosion
using the velocities in the second column, calculate the size of the outer layers of the ejecta
using the temperatures in the third column, calculate the total luminosity of the star
convert the luminosity to an absolute magnitude; you may compare it to the Sun, and assume that the Sun's absolute bolometric magnitude, given in section 3.6 of your textbook
determine the distance modulus to SN 1970G
determine the distance to SN 1970G in parsecs and megaparsecs

The simple calculation you have made should yield something like the value shown in Schmidt, Kirshner and Eastman's table above, in the column labelled D (Mpc). The authors' more complex analysis and modelling of the SN 1970G observations (which appear in the column labelled D_corr yield an estimate of d = 7.6 +1.0 - 2.2 Mpc.

SN 1970G occurred in the galaxy M101, a very pretty and relatively nearby spiral galaxy. Astronomers used the Hubble Space Telescope to study Cepheid variable stars in M101 in the early 1990s, leading to an independent distance estimate. Here's a portion of the abstract from the HST Key Project Team's paper on Cepheids in M101:

Using a Galactic extinction law and the apparent V and I distance moduli, we have found a mean reddening for the M101 sample of E(B- V) = 0.03 mag and a true distance modulus to MI01 of 29.34+/-0.17 mag, corresponding to a distance of 7.4 +/- 0.6 Mpc.

How well does the EPM method seem to work?